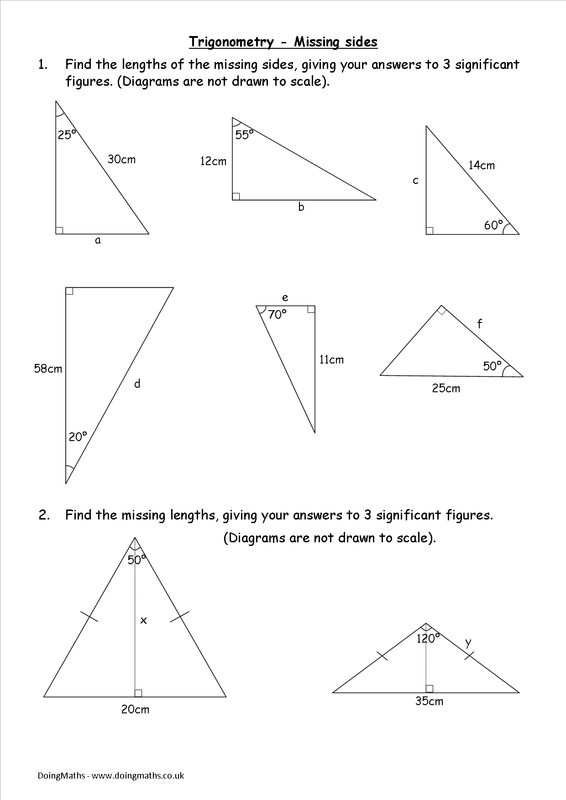
Triangle Congruence: SSS vs SAS Worksheet Solutions
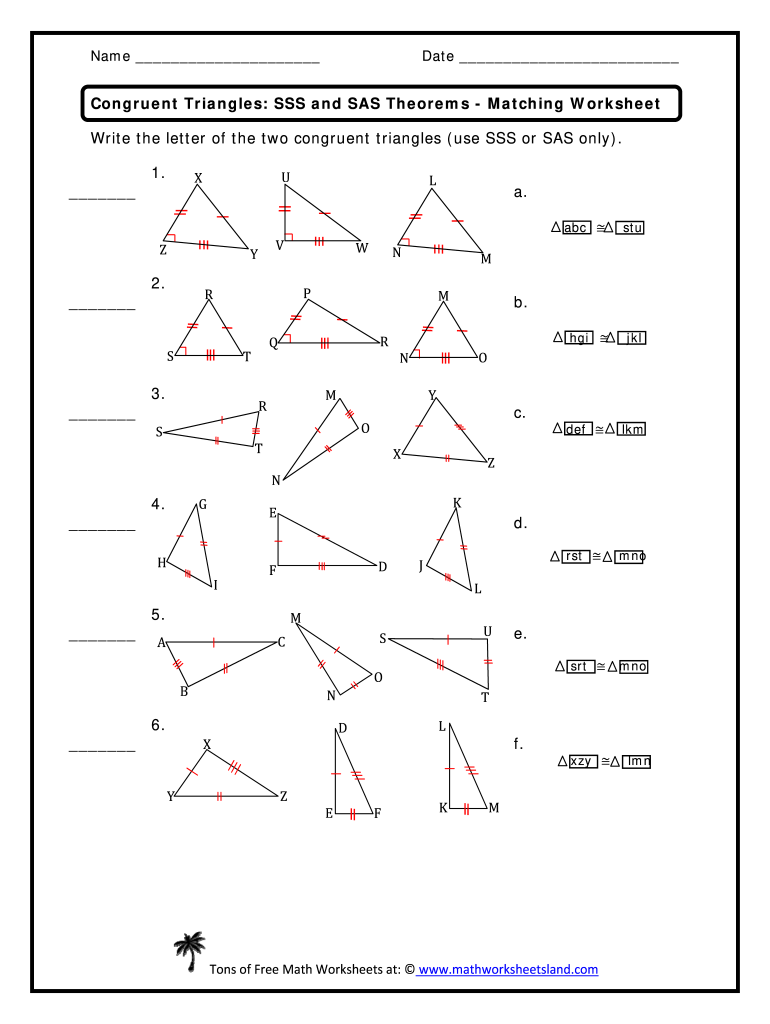
When it comes to understanding triangle congruence, two of the most fundamental criteria are the Side-Side-Side (SSS) and Side-Angle-Side (SAS) postulates. These postulates help mathematicians, students, and enthusiasts determine whether two triangles are identical in shape and size. Let's delve into how these postulates work and provide practical solutions through a worksheet approach.
The Side-Side-Side (SSS) Postulate

SSS states that if three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent. Here’s a breakdown:
- Measure and compare all three sides of both triangles.
- If all sides match in length, the triangles are congruent.
| Triangle A | Triangle B |
|---|---|
| Side 1: 5 units | Side 1: 5 units |
| Side 2: 6 units | Side 2: 6 units |
| Side 3: 7 units | Side 3: 7 units |
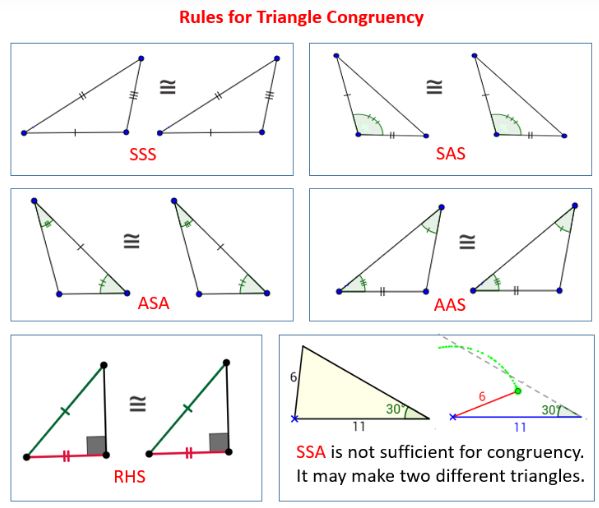
🔄 Note: It’s important to measure sides accurately to ensure congruence through SSS.
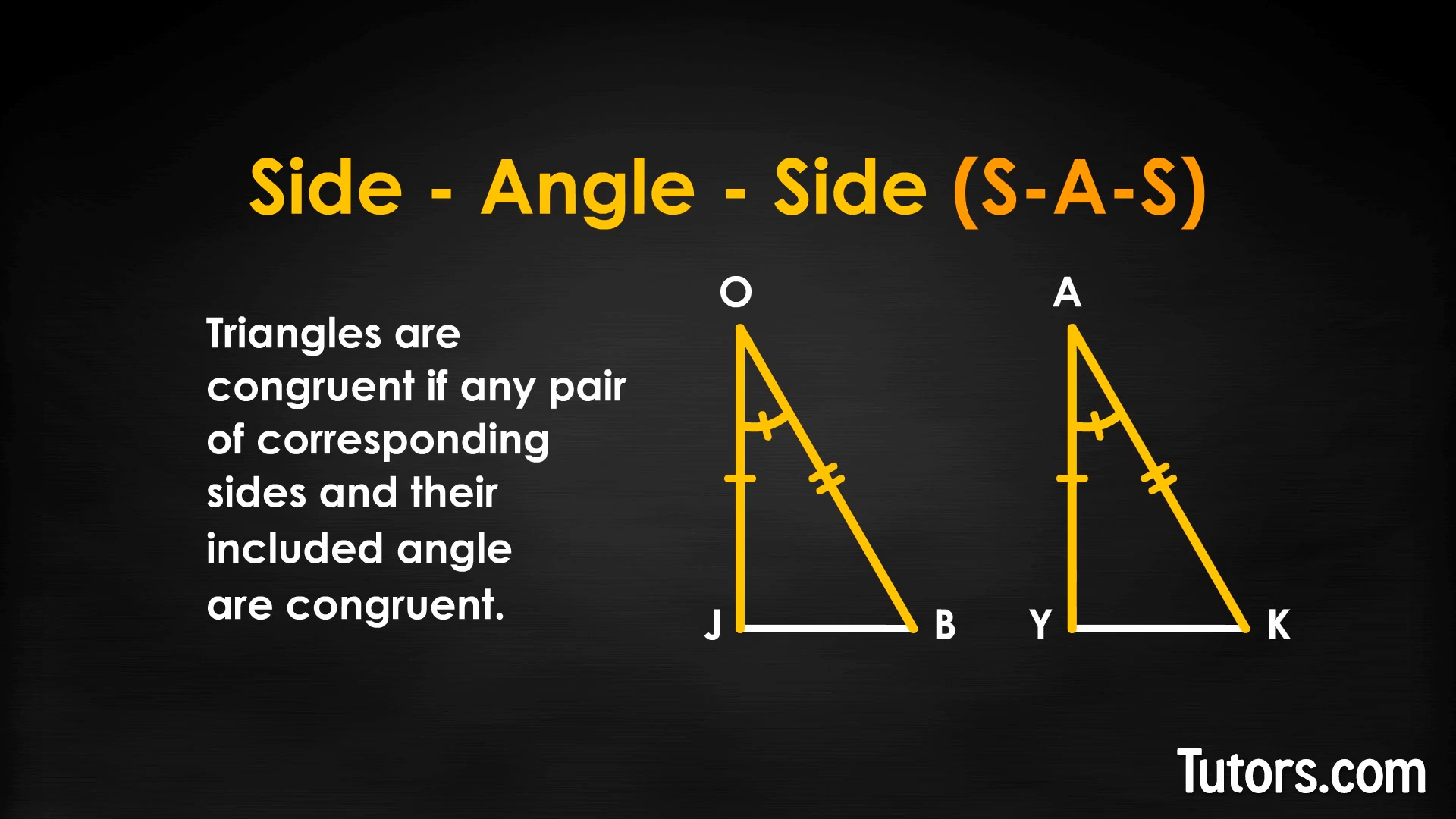
The Side-Angle-Side (SAS) Postulate
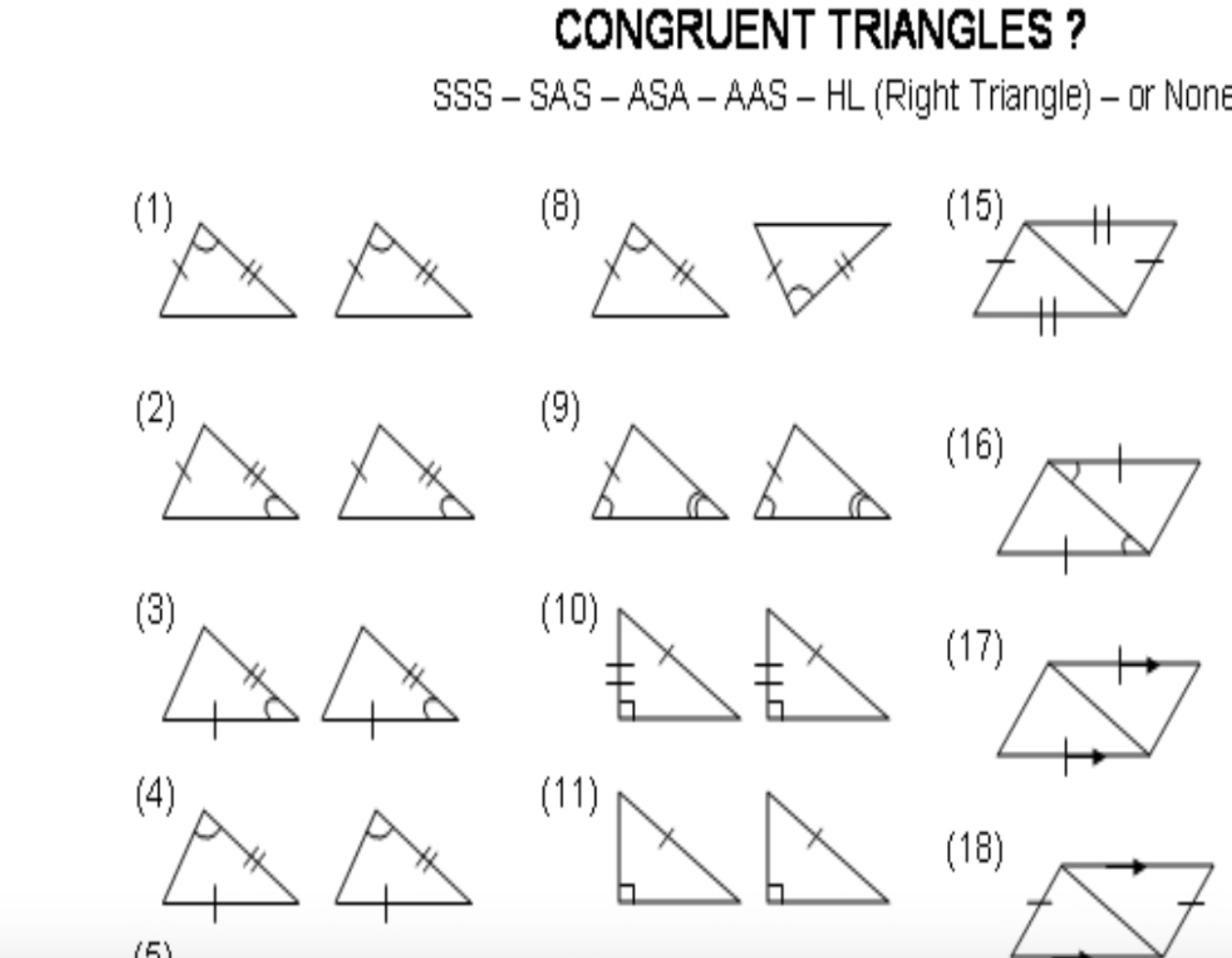
The SAS postulate is slightly different, focusing on:
- Two sides of the triangle and the included angle.
- If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, they are congruent.
Here’s an example:
- Side 1: 4 units
- Included Angle: 60 degrees
- Side 2: 5 units
Compare this to another triangle with the same measurements, and they will be congruent.
Worksheet Solutions
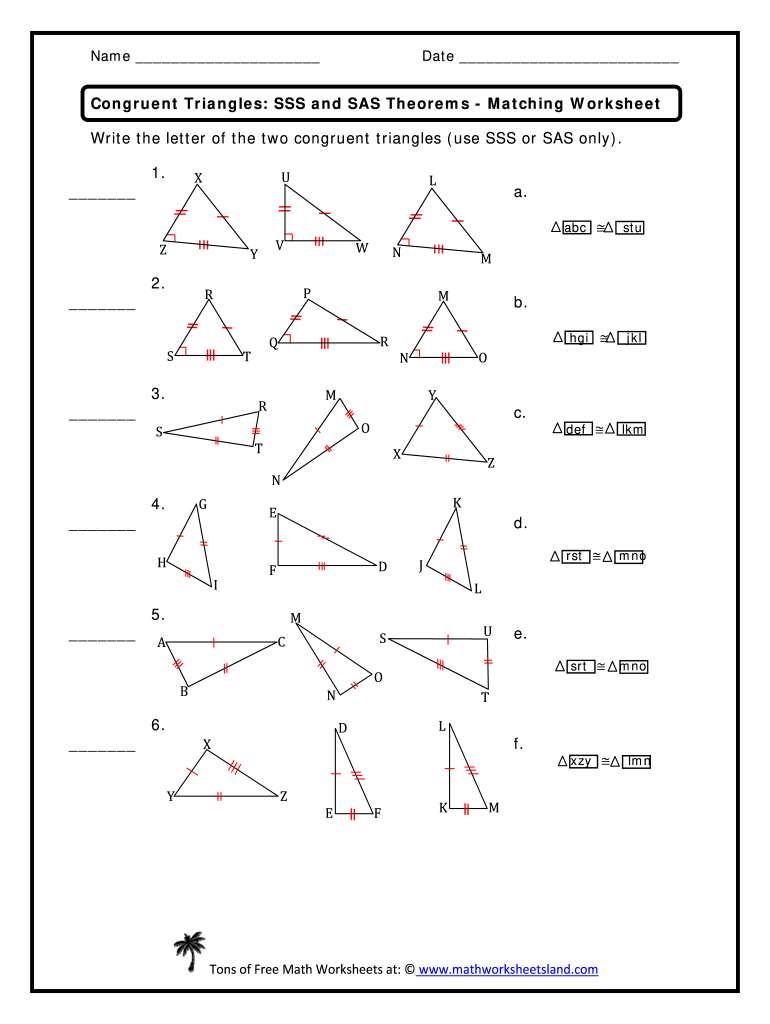
Let’s walk through some practical examples to understand how to apply these postulates in solving problems. Each problem will start with provided measurements or drawings, followed by the solution:
Problem 1: Using SSS
Given two triangles:
- Triangle X: 3, 4, 5
- Triangle Y: 3, 4, 5
Solution: Since all sides of Triangle X match Triangle Y, by the SSS postulate, the triangles are congruent.
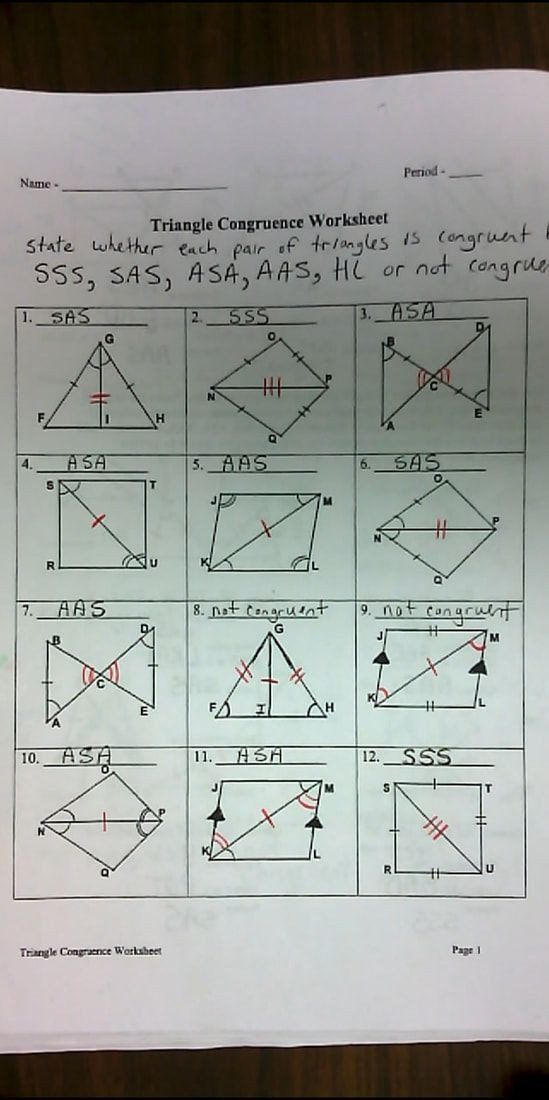
Problem 2: Using SAS
Given two triangles with:
- Triangle A: 5, 30°, 7
- Triangle B: 5, 30°, 8
Solution: Although Triangle A and Triangle B share two sides and an angle, the sides are not the included sides for the same angle. Therefore, they are not congruent by SAS.
Problem 3: Both SSS and SAS

Given two triangles with:
- Triangle C: 7, 8, 10 and 60°
- Triangle D: 7, 8, 10 and 60°
Solution: Both triangles have identical sides and angles. They are congruent by both SSS and SAS postulates.
In Conclusion
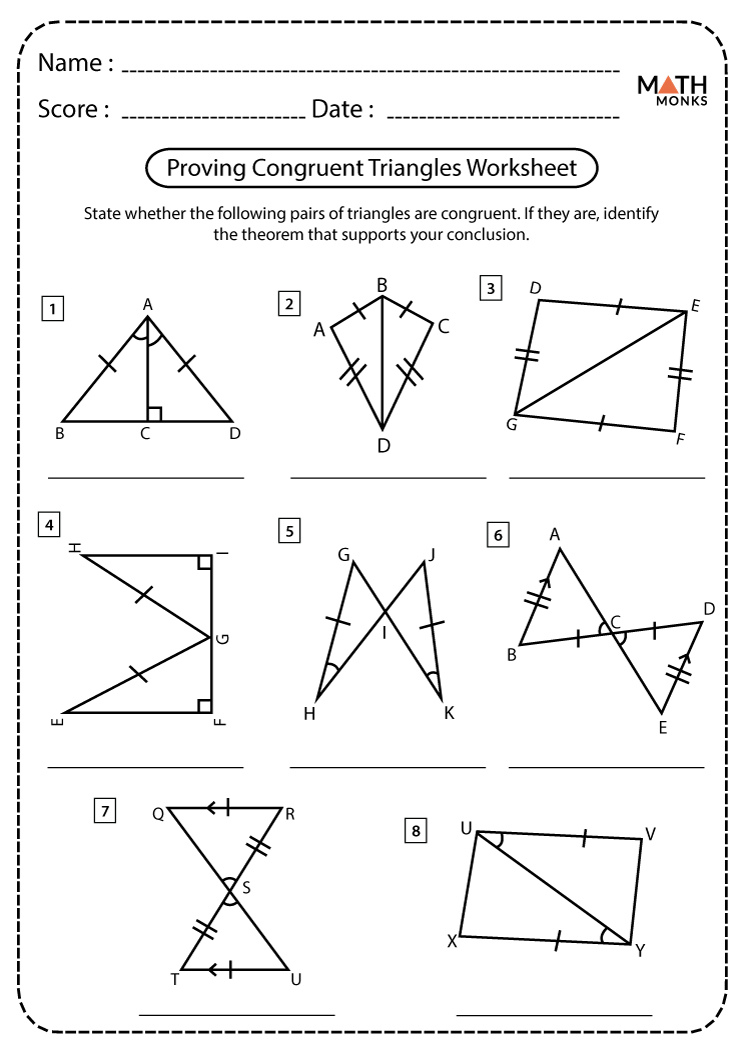
The understanding of triangle congruence, through the lens of SSS and SAS postulates, offers a profound insight into geometric symmetry and equality. These methods provide a systematic approach to verify whether two triangles can be considered identical. By applying these postulates, mathematicians and students alike can swiftly recognize patterns, simplify proofs, and solve problems in Euclidean geometry. Whether you’re proving the congruence of complex polygons or merely identifying congruent shapes in everyday life, SSS and SAS remain indispensable tools in your mathematical toolkit.
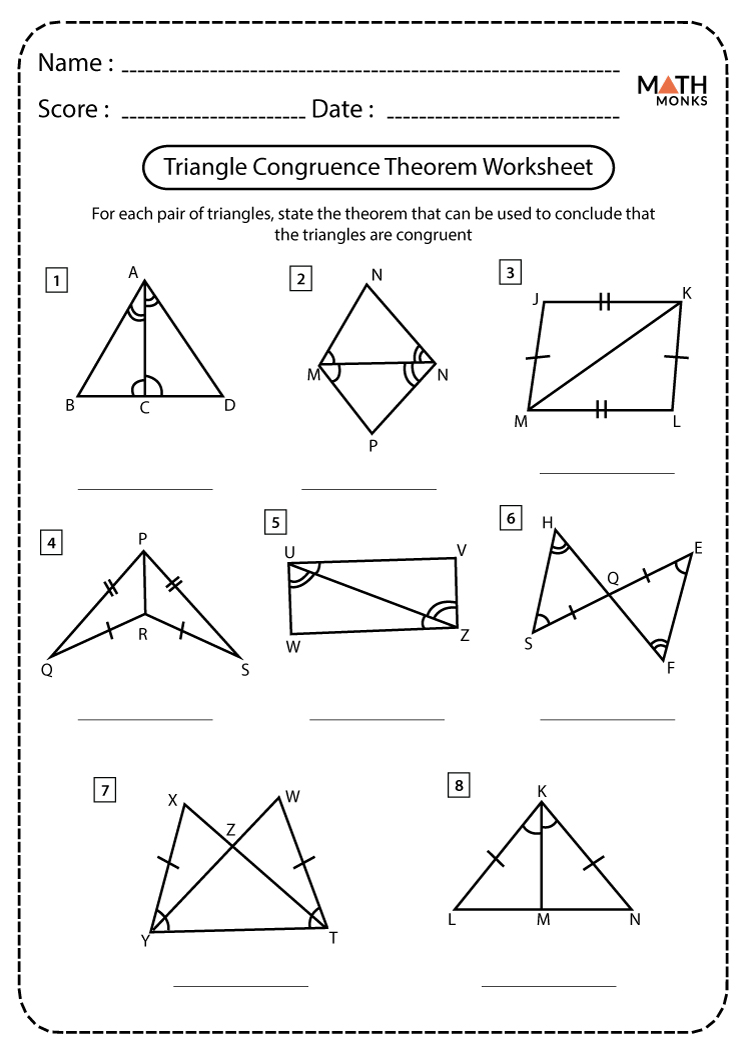
What is the difference between SSS and SAS?
+
SSS (Side-Side-Side) focuses on three sides being equal, while SAS (Side-Angle-Side) requires two sides and the included angle to be equal.
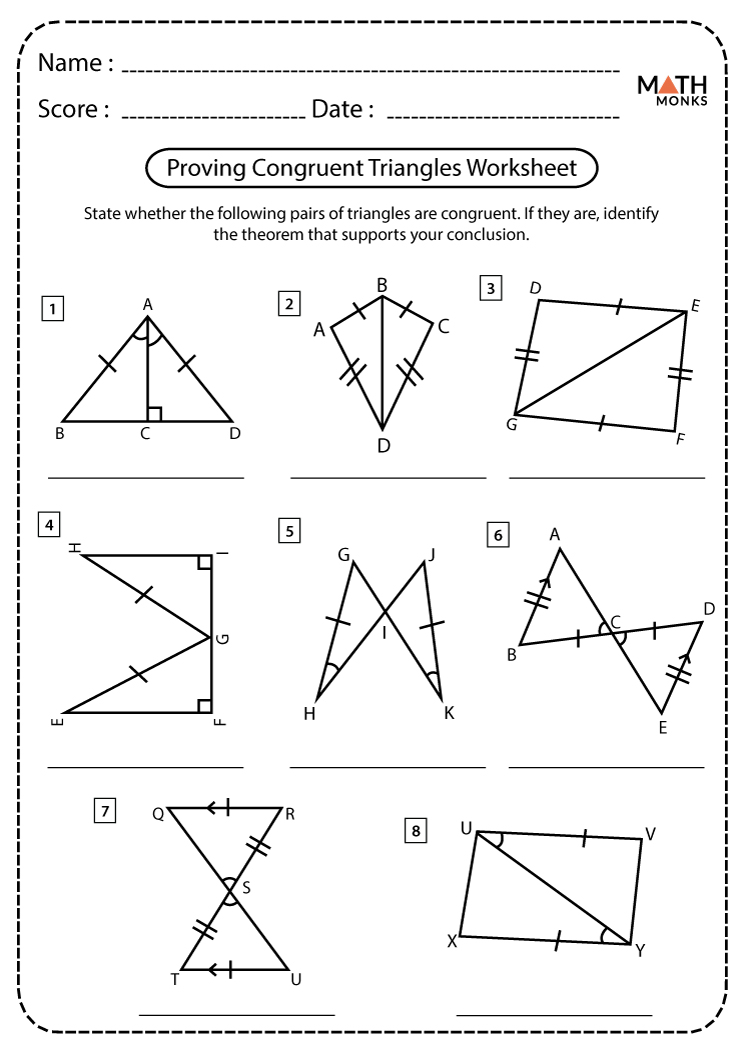
Can you use SAS if the sides are not adjacent to the angle?
+
No, for SAS congruence, the sides must be the ones that form the angle given; otherwise, you can’t assume congruence.
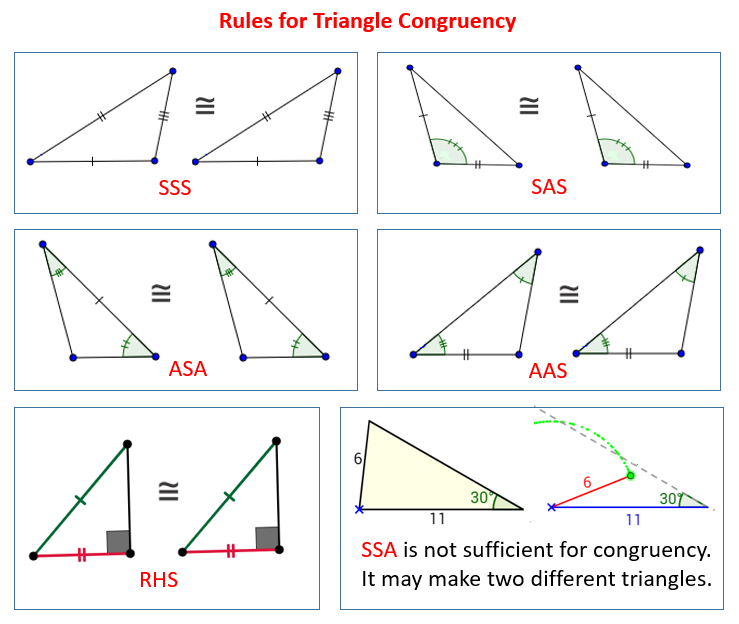
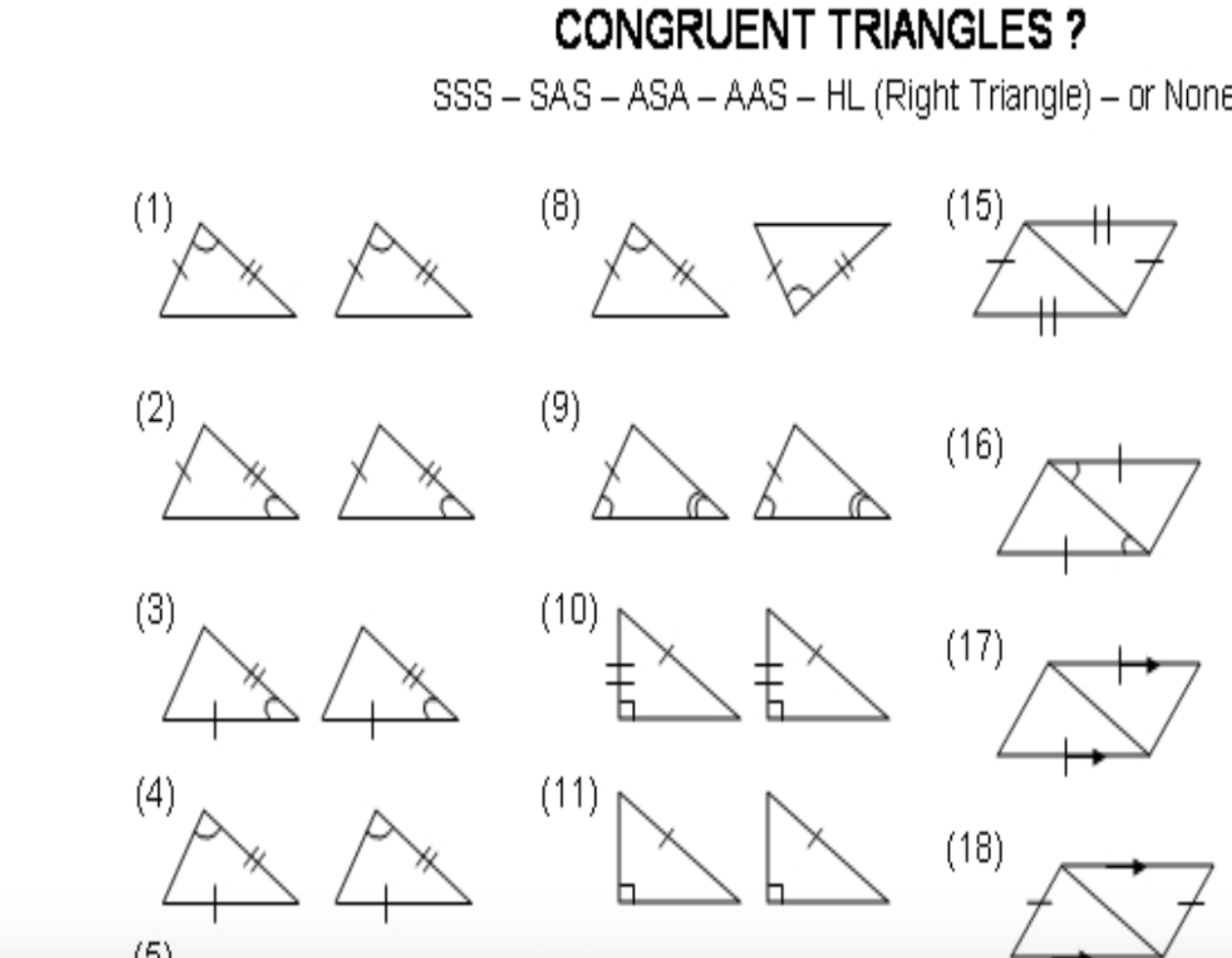
Are there other methods for proving triangle congruence?
+
Yes, besides SSS and SAS, there are ASA (Angle-Side-Angle), AAS (Angle-Angle-Side), and HL (Hypotenuse-Leg) for right triangles.
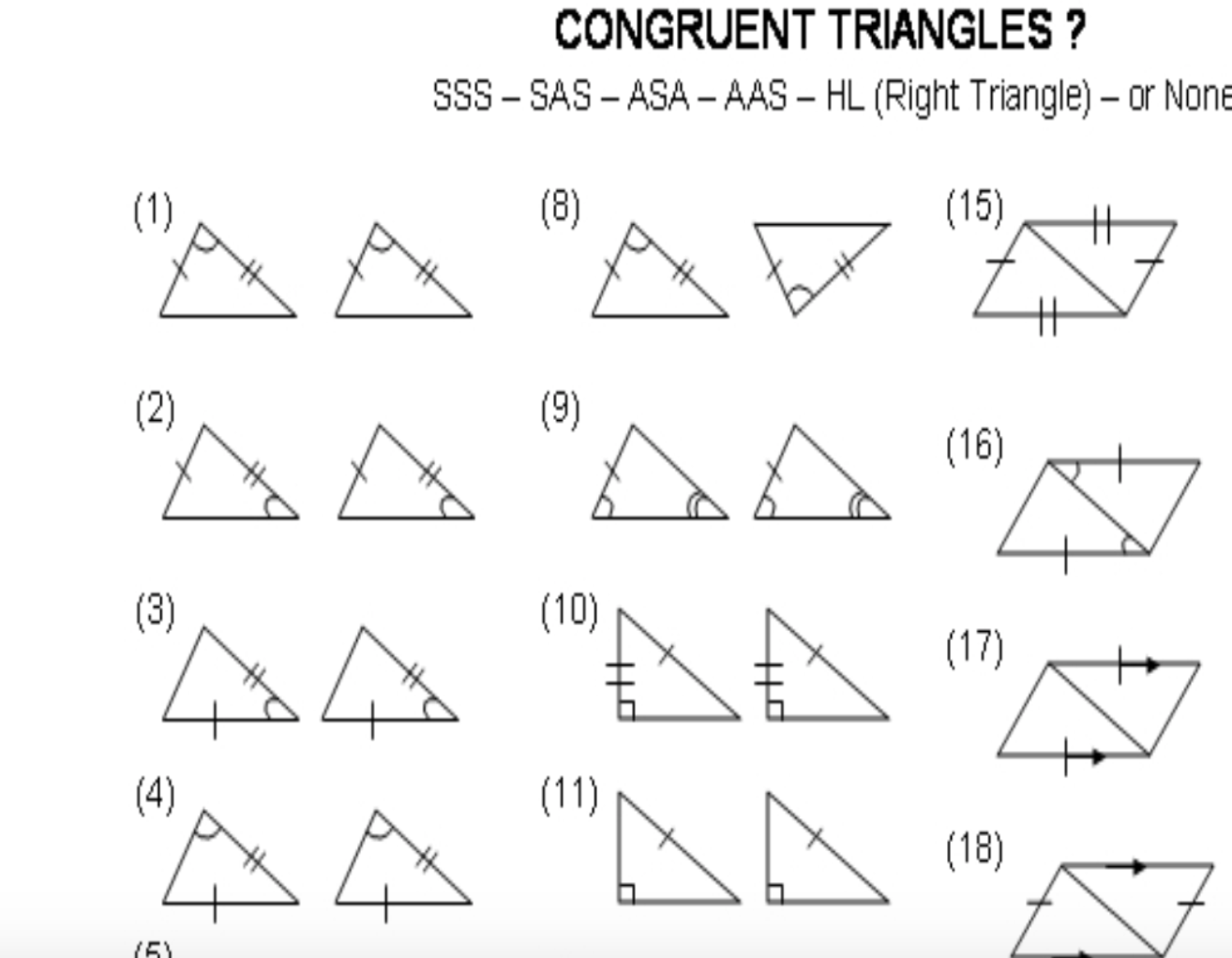
What if I only have two sides of the triangles to compare?
+
If you have two sides and one included angle, you might use SAS, but without an angle, you cannot definitively prove congruence.
Why is the order of sides and angles important in congruence proofs?
+
The order ensures that corresponding parts of triangles are being compared correctly. Misalignment can lead to incorrect conclusions.