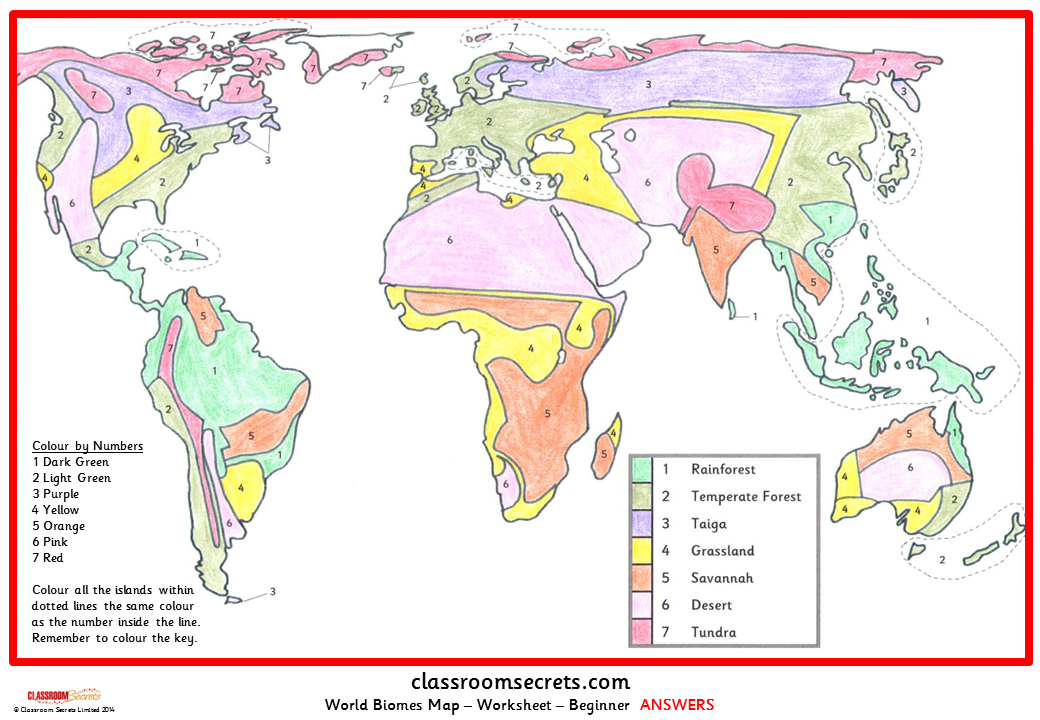
5 Easy Trig Ratio Hacks for Finding Missing Sides
If you've ever found yourself puzzled over trigonometric ratios or struggling with how to find missing sides in triangles, you're not alone. Trigonometry can seem daunting at first, but with the right strategies, you can quickly master the art of calculating sides and angles in any triangle. Here, we’ll explore five easy trig ratio hacks that will simplify your work and make solving trig problems a breeze.
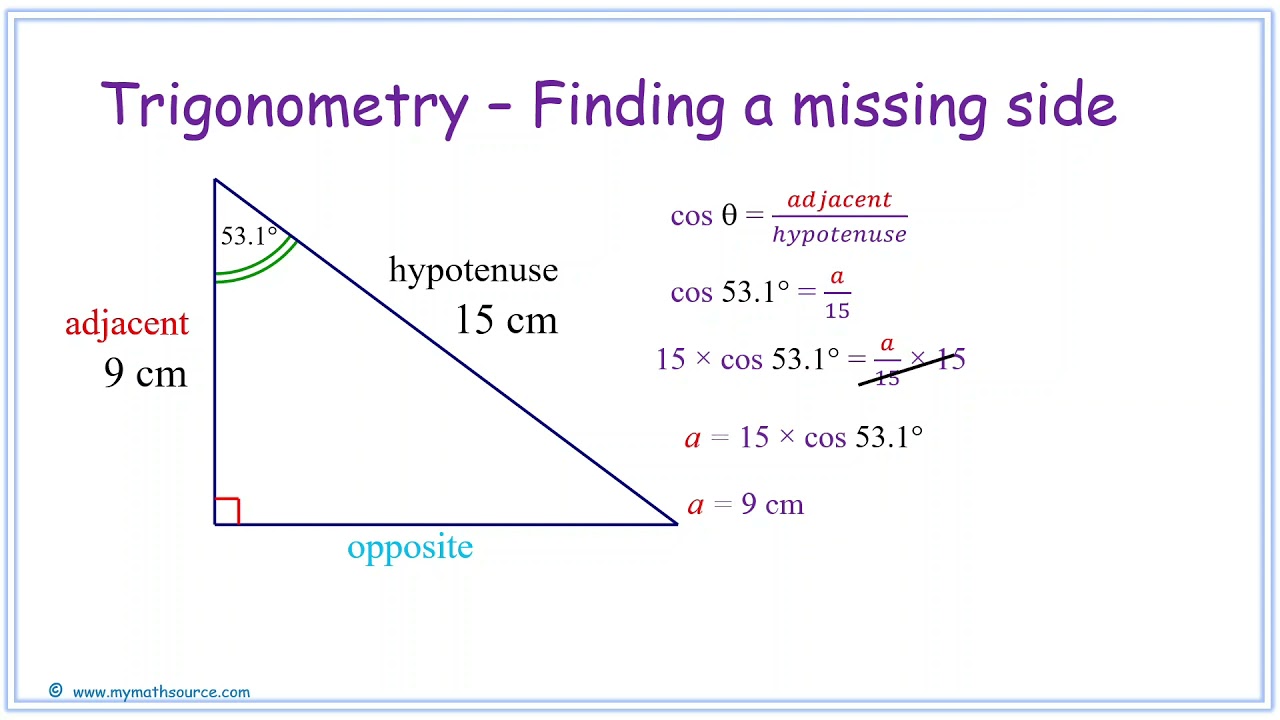
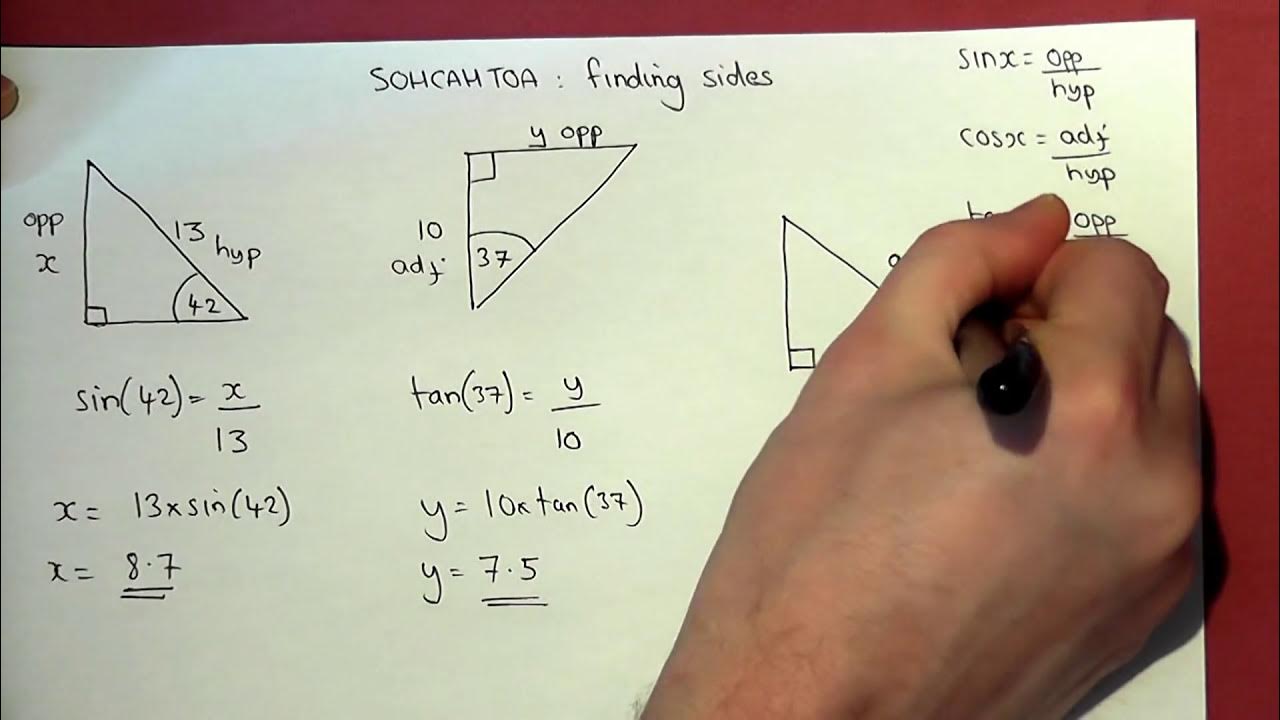
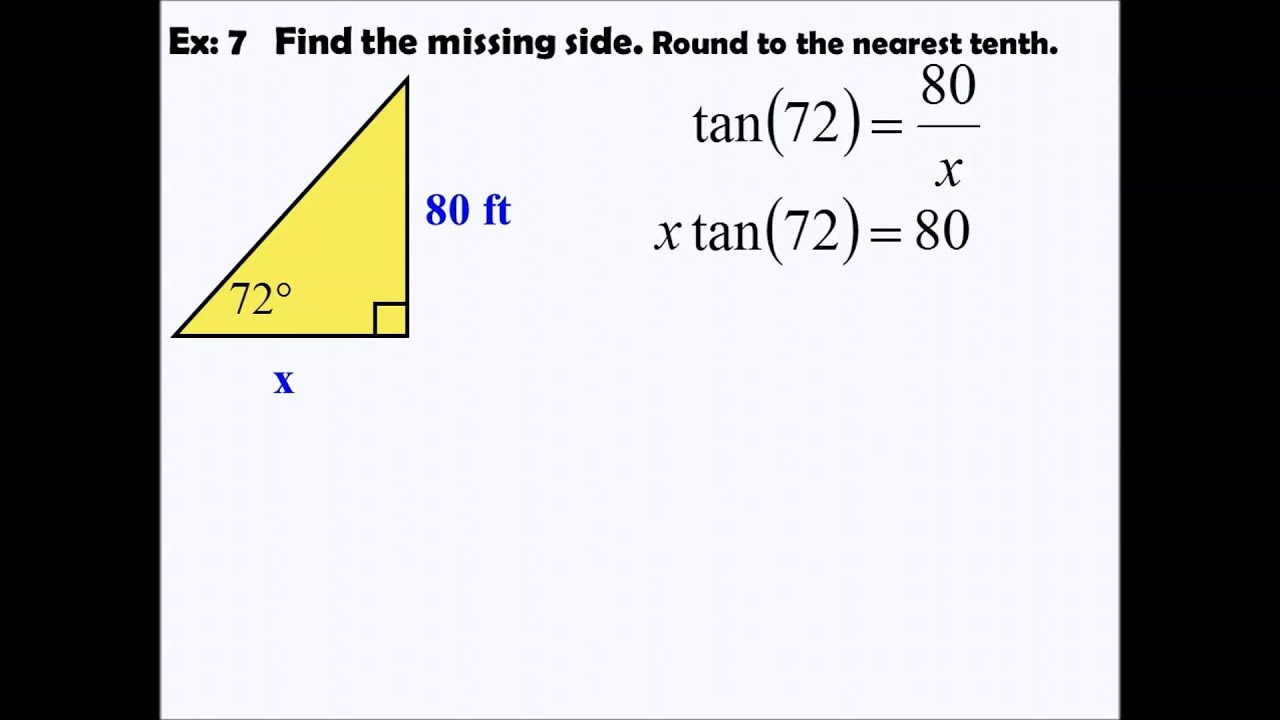
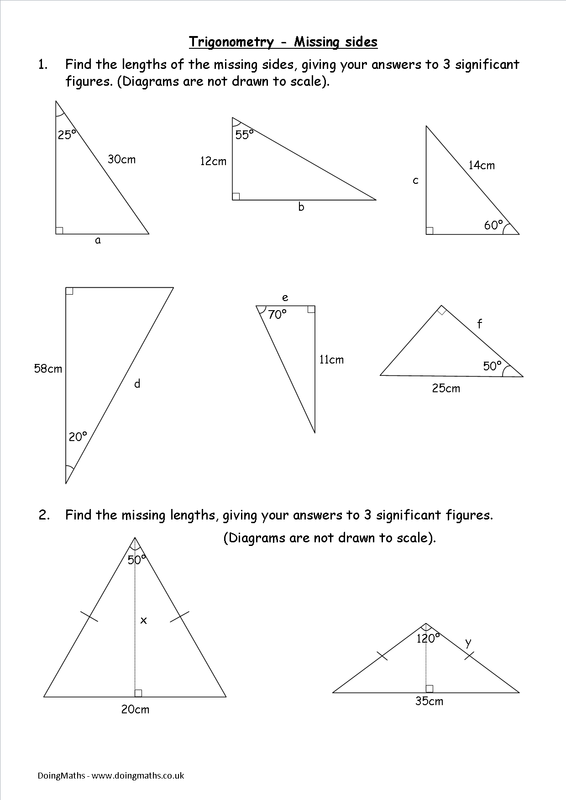
1. Using SOHCAHTOA as Your Foundation

SOHCAHTOA stands for:
- Sine: Opposite over Hypotenuse (SOH)
- Cosine: Adjacent over Hypotenuse (CAH)
- Tangent: Opposite over Adjacent (TOA)
Here's how to use SOHCAHTOA to find missing sides:
- Identify which sides are given in relation to the known angle.
- Select the appropriate ratio (Sine, Cosine, or Tangent) based on what you know.
- Set up the equation using the given ratio and solve for the unknown side.
🔍 Note: SOHCAHTOA applies to right-angled triangles only.
2. The 30-60-90 Triangle Shortcut
If you encounter a triangle where the angles are 30°, 60°, and 90°, here's a quick hack:
- The side opposite the 30° angle is half the hypotenuse.
- The side opposite the 60° angle is equal to the side opposite the 30° angle multiplied by √3.
This special triangle can save you a lot of time in calculations:
| Angle | Side Length |
|---|---|
| 30° | X |
| 60° | X * √3 |
| 90° (Hypotenuse) | 2 * X |

3. Utilizing the Law of Sines and Cosines

While SOHCAHTOA works for right triangles, the Law of Sines and Law of Cosines extend to other triangles:
- Law of Sines:
a / sin(A) = b / sin(B) = c / sin(C) - Law of Cosines:
c² = a² + b² - 2ab cos(C)
These laws are invaluable when:
- You have side-angle-side information (SAS) or angle-side-angle (ASA).
- The triangle is not a right triangle.
4. The Pythagorean Theorem Revisited

Don't forget the foundational:
- Pythagorean Theorem:
a² + b² = c²
While this theorem is basic, you can use it in conjunction with other hacks:
- Find one side if you know the other two sides.
- Check if a triangle is right-angled by verifying if the sum of the squares of two sides equals the square of the third.
✅ Note: The Pythagorean Theorem is a special case of the Law of Cosines when the angle C is 90°.
5. Unit Circle Trigonometry
The Unit Circle can be an invaluable tool for understanding trigonometric functions:
- Use it to quickly find sine, cosine, and tangent values for common angles.
- Realize that for any angle θ:
- Sine is the y-coordinate.
- Cosine is the x-coordinate.
- Tangent can be derived from sine and cosine.
Key Points:
- Unit circle values are exact, making them ideal for quick mental math.
- Extend this to find values for any angle by adding or subtracting 360° or 2π.
By incorporating these five trig ratio hacks into your problem-solving strategy, trigonometry becomes less about memorizing formulas and more about understanding and applying simple principles. From using SOHCAHTOA for right triangles to exploring the unit circle for common angles, these methods streamline the process of finding missing sides. Remember, the key to mastering trigonometry is practice and a clear understanding of each approach. With these hacks, solving trig problems will not only be easier but also more intuitive.
Can SOHCAHTOA be used in any triangle?
+
SOHCAHTOA is specifically for right-angled triangles where you can easily identify the opposite, adjacent, and hypotenuse sides relative to a known angle. For other triangles, you’ll need to use the Law of Sines or Cosines.
What should I do if I only know one side of the triangle?
+
If you only know one side, you’ll need more information. You might need at least one angle or another side length, or you might have to use the Pythagorean Theorem for right triangles or the Law of Cosines for other triangles to proceed.
How does the unit circle help with trigonometric calculations?

+
The unit circle gives you the sine and cosine values of any angle by looking at the coordinates of a point on its circumference. Tangent can then be derived from these values, making the unit circle a powerful tool for understanding and solving trig problems visually.