7 Quick Answers to Algebra 2 Vertex Form Problems

Algebra 2 is often where students start to grapple with more complex mathematical concepts, including those involving quadratic equations in vertex form. This format, which is presented as f(x) = a(x - h)^2 + k , where (h, k) represents the vertex of the parabola, is crucial for both graphical and analytical understanding. Whether you're a student revising for an exam or an enthusiast looking to solidify your grasp on algebra, let's dive into seven common problems and their quick answers concerning vertex form in Algebra 2.
Understanding Vertex Form

Before we tackle specific problems, let's ensure we're all on the same page about what vertex form represents:
- Vertex: The point (h, k) is where the parabola reaches its minimum or maximum point.
- Symmetry: The axis of symmetry is a vertical line passing through the vertex x = h .
- Direction: If a > 0 , the parabola opens upward; if a < 0 , it opens downward.
🗣 Note: Knowing the vertex form can significantly simplify problems involving the maximum or minimum values of quadratic functions.
Problem 1: Converting from Standard Form to Vertex Form

Problem: Convert f(x) = x^2 + 6x - 7 to vertex form.
Answer: To convert, follow these steps:
- Identify a , b , and c from the standard form ax^2 + bx + c .
- Find h using the formula h = -b / (2a) . Here, h = -6 / 2 = -3 .
- Substitute h into the equation to find k : k = f(h) = f(-3) = (-3)^2 + 6(-3) - 7 = -16 .
- Write the equation in vertex form: f(x) = (x + 3)^2 - 16 .
🗣 Note: This conversion method uses the concept of completing the square, which can be tricky but is essential for many algebraic processes.
Problem 2: Finding the Maximum or Minimum Value

Problem: Determine the maximum or minimum value of f(x) = -2(x - 3)^2 + 4 .
Answer: Since a = -2 , the parabola opens downward, meaning there is a maximum value at the vertex:
- The maximum value k is 4.
Problem 3: Identifying the Domain and Range
Problem: What are the domain and range of the function f(x) = (x + 2)^2 - 1 ?
Answer:
- Domain: All real numbers since x can take any value.
- Range: The function reaches a minimum at the vertex, so y \geq -1 .
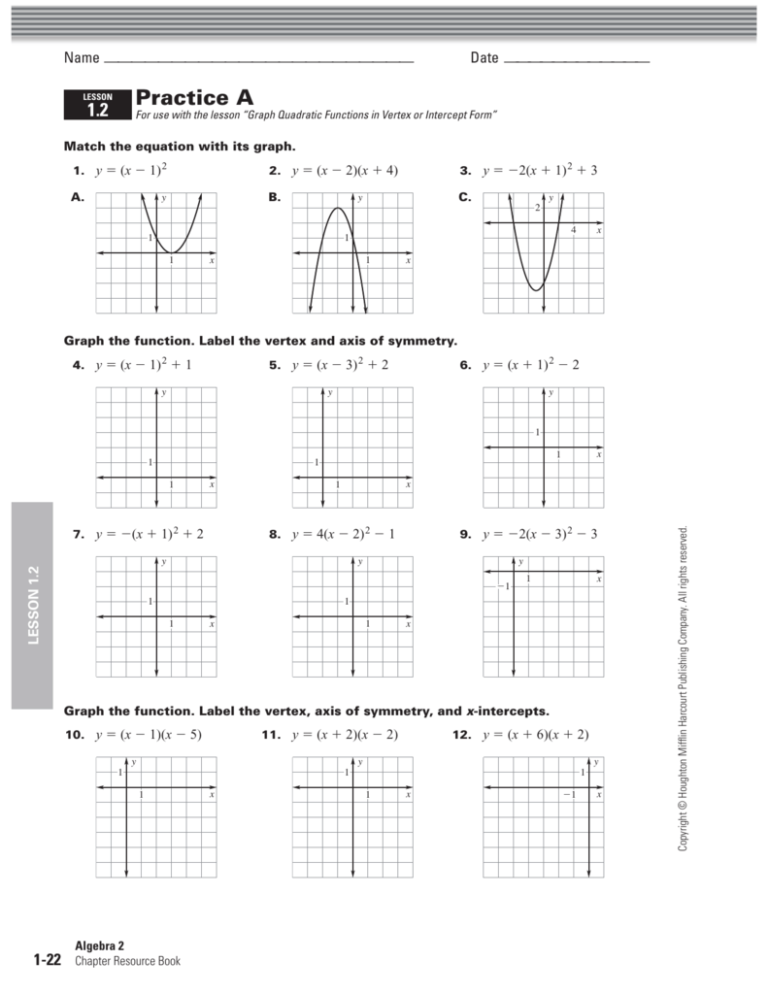
Problem 4: Finding the Vertex

Problem: Find the vertex of f(x) = 2(x - 4)^2 + 3 .
Answer: The vertex is directly provided in the equation:
- h = 4 , k = 3 , thus the vertex is at (4, 3).
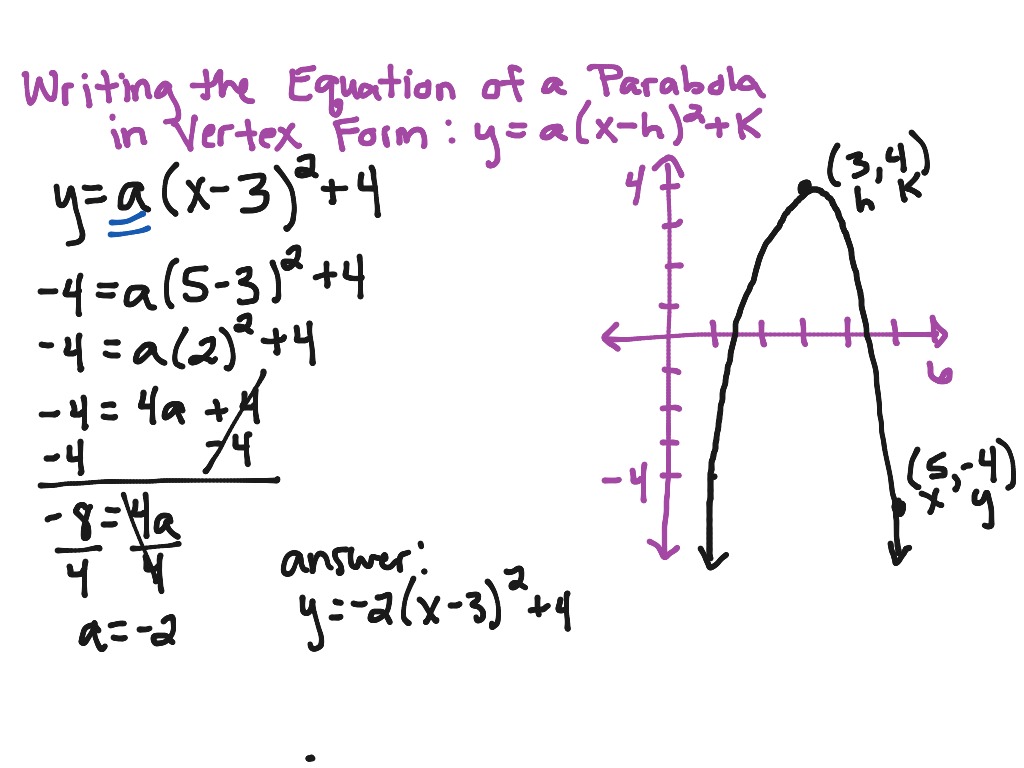
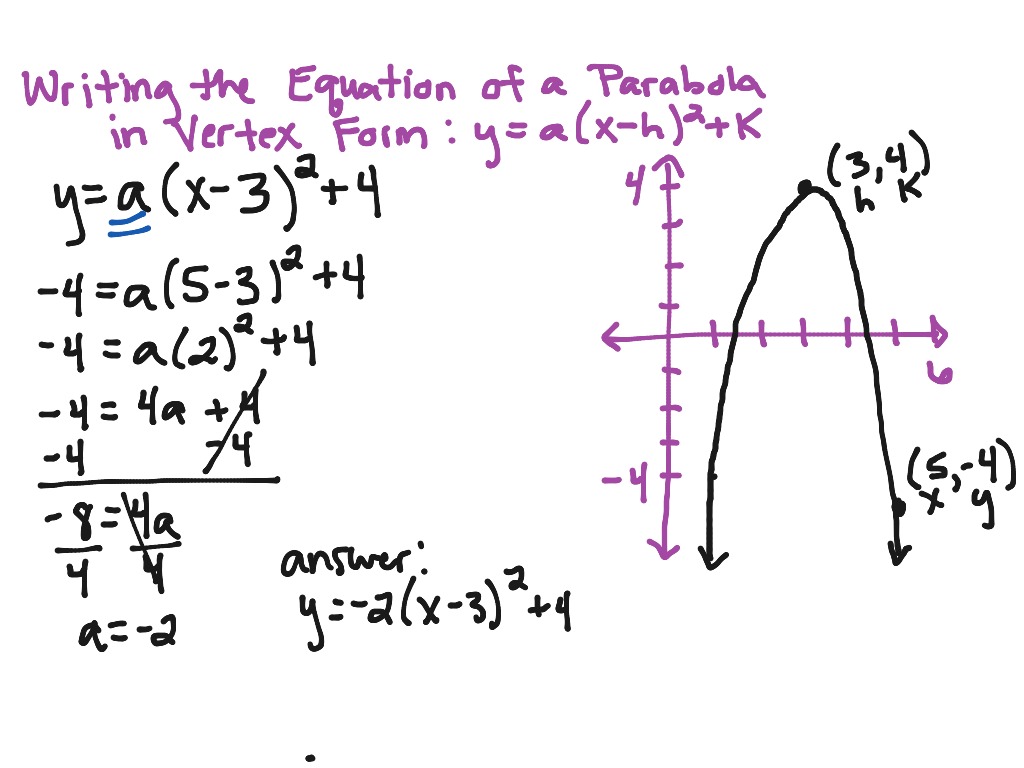
Problem 5: Converting Vertex Form to Standard Form
Problem: Convert f(x) = (x - 5)^2 + 7 to standard form.
Answer:
- Expand (x - 5)^2 : x^2 - 10x + 25 .
- Add the constant k : f(x) = x^2 - 10x + 25 + 7 = x^2 - 10x + 32 .
Problem 6: Solving for a Given Point on the Parabola
Problem: Given the function f(x) = 3(x - 1)^2 + 2 , find f(2) .
Answer: Substitute x = 2 into the equation:
- f(2) = 3(2 - 1)^2 + 2 = 3(1)^2 + 2 = 5 .
Problem 7: Intercepting the x-Axis
Problem: Find the x-intercepts of f(x) = (x + 4)(x - 6) .
Answer: Set the equation to zero:
- (x + 4)(x - 6) = 0
- Leading to x = -4 or x = 6 .
In Algebra 2, understanding the vertex form of quadratic equations provides an invaluable tool for visualizing and solving quadratic functions. Each problem here showcases how different aspects of a parabola can be analyzed or derived from its vertex form, enhancing your algebra skills in real-world applications and higher mathematics. Whether you're calculating maximum heights in physics or profit analysis in economics, the vertex form proves its utility.
What is the vertex form used for in Algebra 2?
+
The vertex form of a quadratic equation, ( f(x) = a(x - h)^2 + k ), is particularly useful for identifying the vertex (maximum or minimum point) of a parabola, the axis of symmetry, and to quickly sketch the graph of the parabola.
Can I find the roots of a quadratic equation from vertex form?

+
Yes, but it’s typically more efficient to use the standard form. However, you can derive the roots from vertex form by setting the equation to zero and solving for ( x ).
How does changing the value of ( a ) in the vertex form affect the parabola?
+
The coefficient ( a ) determines the direction and stretch or compression of the parabola. If ( a > 0 ), the parabola opens upward, and if ( a < 0 ), it opens downward. Increasing ( |a| ) makes the parabola narrower, and decreasing ( |a| ) makes it wider.