5 Easy Steps to Subtract Fractions with Regrouping

Introduction to Subtracting Fractions with Regrouping

Subtracting fractions with regrouping might seem intimidating at first, but once you break it down into manageable steps, it becomes much more approachable. This process involves converting mixed numbers into improper fractions, finding common denominators, and sometimes regrouping to ensure subtraction is possible. Here's how you can master this skill in five easy steps:
Step 1: Convert Mixed Numbers to Improper Fractions

- Multiply the whole number by the denominator of the fraction.
- Add this result to the numerator, keeping the denominator unchanged.
- Example: For 3 \frac{1}{4}:
- Multiply 3 \times 4 = 12
- Add 12 + 1 = 13
- Result: \frac{13}{4}
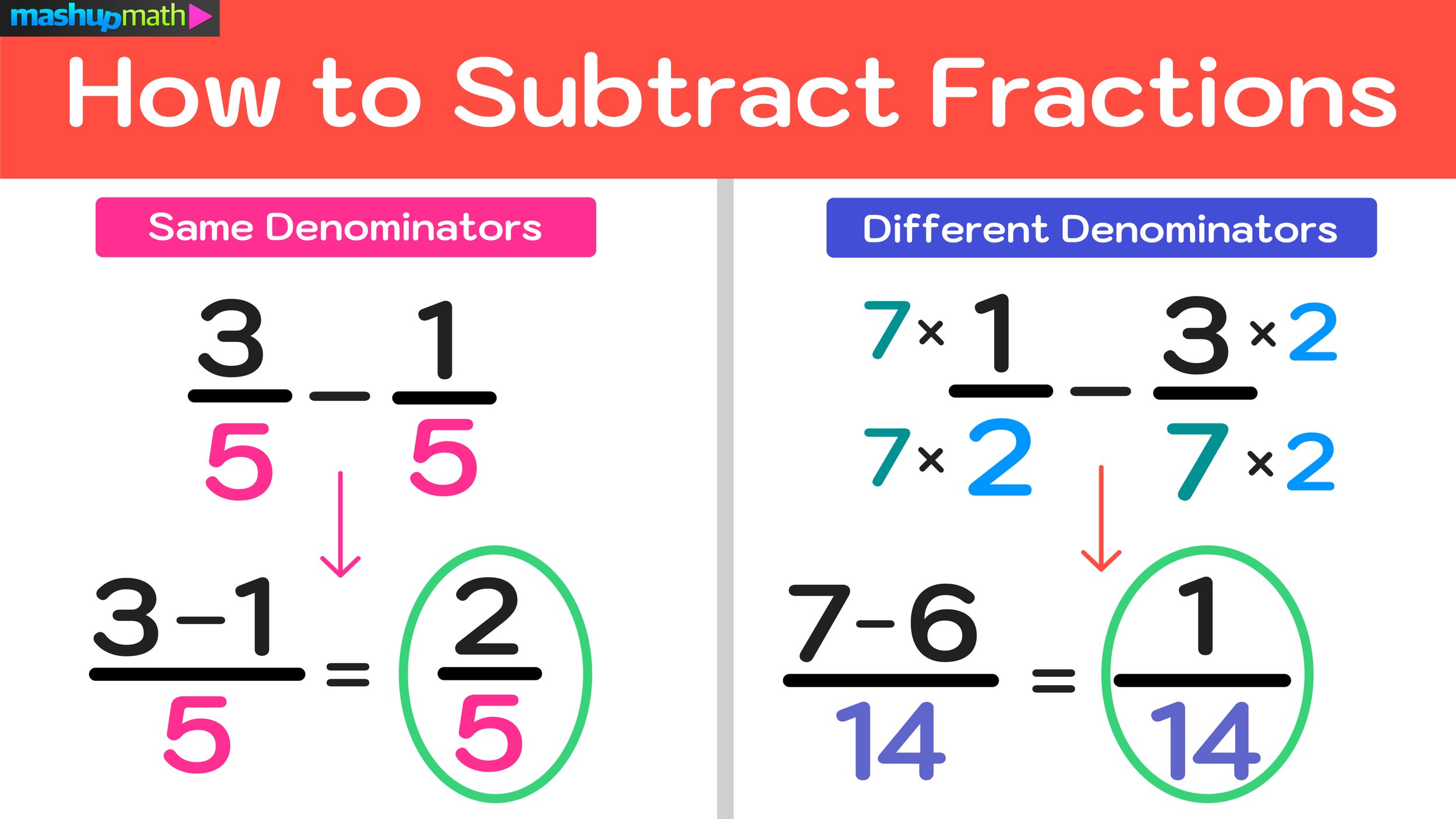
Step 2: Find a Common Denominator

When subtracting fractions, they must share the same denominator to simplify the process. Here's how to do it:
- Identify the least common multiple (LCM) of the denominators.
- Multiply both the numerator and the denominator of each fraction by the necessary factor to reach the LCM.
- Example: If you have \frac{13}{4} and \frac{5}{6}:
- LCM of 4 and 6 is 12.
- \frac{13}{4} = \frac{39}{12} (multiply numerator and denominator by 3)
- \frac{5}{6} = \frac{10}{12} (multiply numerator and denominator by 2)
Step 3: Adjust Numerators for Subtraction
After finding a common denominator, you might need to adjust the numerators if subtracting the smaller fraction from the larger one is not possible directly:
- If the numerator of the minuend (the number from which you're subtracting) is smaller than the subtrahend (the number you're subtracting), you'll need to borrow from the whole number part.
- Borrowing means you take 1 from the whole number, convert it to the fraction, and then add it to your current numerator.
- Example: With \frac{13}{12} and \frac{10}{12}:
- Since 13 - 10 = 3, there's no need to regroup here.
- If you had to, borrowing would look like this: Take 1 from the whole number, make it \frac{12}{12}, add to the fraction, resulting in \frac{25}{12} - \frac{10}{12} = \frac{15}{12}.
Step 4: Perform the Subtraction

- Subtract the numerator of the subtrahend from the numerator of the minuend, keeping the denominator the same.
- Example: \frac{39}{12} - \frac{10}{12} = \frac{29}{12}.
- Reduce the resulting fraction if possible.
Step 5: Convert Back to a Mixed Number

If your result is an improper fraction, convert it back to a mixed number for a complete subtraction process:
- Divide the numerator by the denominator.
- The quotient becomes the whole number part.
- The remainder becomes the numerator of the new fraction, and the denominator remains the same.
- Example: \frac{29}{12} -> Quotient 2, Remainder 5, so 2 \frac{5}{12}.
📌 Note: When dealing with fractions where the common denominator does not lead to direct subtraction, regrouping becomes essential. This involves borrowing from the whole number to increase the fraction you're subtracting from.
Summary

Subtracting fractions with regrouping can be broken down into simple steps: converting mixed numbers to improper fractions, finding a common denominator, adjusting numerators as necessary through borrowing, performing the subtraction, and converting the result back to a mixed number. With practice, these steps will become second nature, allowing you to tackle even complex subtraction scenarios effortlessly. This skill is crucial not only for arithmetic but also for understanding more advanced mathematical concepts.
Why do we need to find a common denominator when subtracting fractions?

+
Finding a common denominator ensures that the fractions have the same base or size, allowing for direct subtraction or addition without changing the value of the fractions.
What if I have two fractions with different denominators?
+
If the fractions have different denominators, you must convert both fractions to equivalent fractions with a common denominator before you can subtract or add them.
Can I skip borrowing when subtracting fractions?

+
Not always. If the numerator of the fraction you’re subtracting from is smaller than the one you’re subtracting, you need to borrow from the whole number part to ensure the subtraction is valid.