Trigonometry Made Easy: Calculate Sides Worksheet T3

Understanding trigonometry can be a daunting task for many students, but with the right approach, it becomes significantly easier. Today, we're going to dive into trigonometry with a focus on calculating the sides of triangles using trigonometric ratios. Whether you're struggling with trigonometry or simply looking to brush up on your skills, this worksheet guide is designed to make the concept straightforward and accessible.
Why Trigonometry Matters

Trigonometry is not just an abstract concept limited to math classrooms; it’s fundamental in fields like engineering, physics, architecture, and even in daily life for things like understanding how to aim a satellite dish or design the pitch of a roof. Here’s why mastering trigonometry is essential:
- Engineering Applications: Engineers use trigonometry to calculate distances, angles, and dimensions, which are crucial for designing structures and understanding forces in mechanics.
- Navigation: Trigonometry helps pilots, sailors, and even those on land to understand their position relative to a destination or a landmark through angular measurements.
- Astronomy: Astronomers use it to measure distances between celestial bodies, planetary motions, and the orbits of satellites.
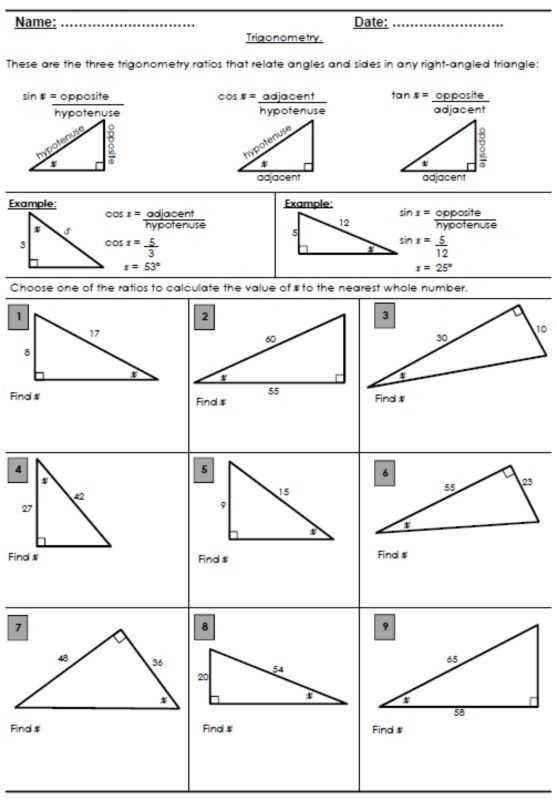
Basic Trigonometric Ratios

Before we delve into the worksheet, let’s recap the basic trigonometric ratios you’ll encounter:
- Sine (sin): Opposite/Hypotenuse
- Cosine (cos): Adjacent/Hypotenuse
- Tangent (tan): Opposite/Adjacent
These ratios are derived from the properties of right triangles, where one angle is always 90 degrees.
The Trigonometry Sides Calculation Worksheet

We’re now going to work through a worksheet focused on calculating the sides of a right triangle using these trigonometric functions. Here’s a step-by-step approach:
Step 1: Identify Known Quantities

Start by determining what you know:
- The length of one side
- At least one angle (other than 90°)
Example: Let’s say we have a triangle with an angle of 30°, and one known side (hypotenuse) of 10 units.
Step 2: Decide Which Trigonometric Function to Use

Depending on which side you’re solving for, choose the appropriate ratio:
- If you’re finding an opposite side, use sin.
- For the adjacent side, use cos.
- To calculate the hypotenuse or the tangent of an angle, use tan.
Step 3: Set Up the Equation

Using our example:
- If we want the opposite side, we use:
sin(30°) = opposite/10
Since sin(30°) is 0.5, we can solve for the opposite side:
opposite = 10 * sin(30°) = 10 * 0.5 = 5 units
Step 4: Solve for the Unknown Side
Calculate the unknown side:
- If looking for the adjacent side, use:
cos(30°) = adjacent/10 - Since
cos(30°)is approximately0.866,adjacent = 10 * 0.866 ≈ 8.66 units
🔍 Note: When solving for the unknown side, ensure that you are using the correct side relative to the angle in question.
Step 5: Check Your Work

Always check your calculations by either using the Pythagorean Theorem or by verifying the angles and sides using a trigonometric calculator:
- The sum of the squares of the sides should equal the square of the hypotenuse:
5² + (8.66)² = 25 + 75.01 ≈ 100, confirming the hypotenuse is approximately 10.
The use of a table can be beneficial when dealing with multiple similar calculations:
| Angle (°) | sin | cos | tan |
|---|---|---|---|
| 30 | 0.5 | 0.866 | 0.577 |
| 45 | 0.707 | 0.707 | 1 |
| 60 | 0.866 | 0.5 | 1.732 |
📚 Note: This table only lists a few angles; for more precise work, you'll need a full trigonometric table or a scientific calculator.
By following these steps and utilizing tools like tables or calculators, you can solve for the sides of triangles with confidence.
Understanding the intricacies of trigonometry opens up a world of possibilities. From simplifying calculations in physics to solving practical problems in everyday life, mastering these techniques provides you with both technical knowledge and problem-solving skills. Remember, practice makes perfect. Work through numerous examples to internalize the process of identifying sides, selecting the correct trigonometric ratio, and solving for unknowns.
Why do we use the sine, cosine, and tangent ratios in trigonometry?

+
These ratios are essential because they define relationships between angles and the sides of a right triangle. They provide a standardized way to calculate unknown sides or angles, making problem-solving consistent and efficient.
How can I remember which ratio to use?

+
One common mnemonic is SOHCAHTOA:
- Sine = Opposite/Hypotenuse (SOH)
- Cosine = Adjacent/Hypotenuse (CAH)
- Tangent = Opposite/Adjacent (TOA)
What if my triangle isn’t a right triangle?

+
In non-right triangles, you can use laws like the Law of Sines or Cosines, or you can decompose the triangle into multiple right triangles to apply basic trigonometry rules.



