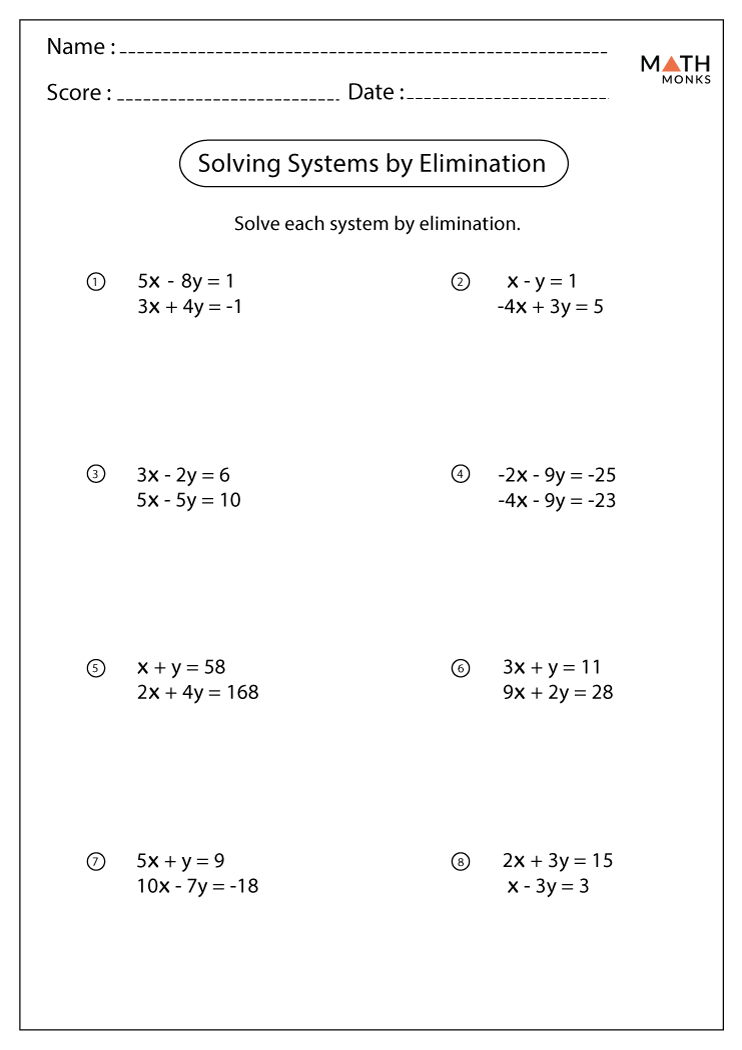
Solve Systems of Equations Worksheet: Master Math Easily

Understanding systems of equations is essential for tackling various mathematical problems in algebra, geometry, and beyond. Whether you're a student preparing for an exam, a professional in need of quick solutions, or someone simply looking to sharpen their math skills, mastering systems of equations can be done with ease through systematic approaches and practice. Here's how you can simplify the process and become adept at solving these systems.

What Are Systems of Equations?

A system of equations involves multiple equations with multiple variables. Solving these systems means finding the values of these variables that make all the equations true simultaneously. Here's a brief overview:

• Linear Systems: Equations that can be represented by straight lines on a graph.
• Nonlinear Systems: Includes quadratic, exponential, or trigonometric equations which might not be straight lines.
• Consistent: When a solution exists.
• Inconsistent: When no solution exists due to contradictions.
• Dependent: When there are infinitely many solutions due to equations being multiples of each other.

Understanding these classifications helps in determining the approach for solving.

Methods to Solve Systems of Equations

There are several methods to solve systems of equations:

• Substitution: Substitute one variable from one equation into another to eliminate it.
• Elimination: Add or subtract equations to eliminate one variable.
• Graphing: Plot each equation and find the intersection point(s) of the graphs.
• Matrix Method: Use matrices to solve systems by Gaussian elimination or the inverse matrix method.

Each method has its strengths, which we'll explore in detail:

Substitution Method

The substitution method is particularly useful for systems where one equation is easily solved for one variable. Here are the steps:

1. Solve one equation for one variable.
2. Substitute that expression into the other equation(s).
3. Solve for the remaining variable(s).
4. Back-substitute to find the other variable(s).

Here's an example:

2x + y = 10
   x - 2y = 1

1. From the first equation, solve for y: y = 10 - 2x
2. Substitute into the second equation: x - 2(10 - 2x) = 1
3. After simplification, we get x + 4x = 21, thus x = 3
4. Back-substitute: y = 10 - 2(3) = 4

🔍 Note: The substitution method is particularly useful when one variable is already isolated in one of the equations.

Elimination Method

The elimination method aims to remove one variable by adding or subtracting equations:

1. If necessary, adjust equations to have the same coefficient for one variable.
2. Add or subtract the equations to eliminate that variable.
3. Solve for the remaining variable.
4. Substitute back to find the other variable(s).

Consider the same system of equations:

2x + y = 10
   x - 2y = 1

1. Multiply the second equation by 2 to align coefficients of x: 2(x - 2y) = 2(1) or 2x - 4y = 2
2. Subtract the first equation from this new equation: (2x - 4y) - (2x + y) = 2 - 10
3. Simplify: -5y = -8, so y = 8/5
4. Back-substitute 2x + (8/5) = 10 to find x = 6

The choice between substitution and elimination often depends on which makes calculations simpler.

Graphing Method

Graphing is intuitive and useful for visualizing solutions:

1. Plot each equation on a coordinate grid.
2. Find where the lines intersect (if they do).
3. The intersection point(s) are the solutions.

This method helps in understanding the nature of solutions visually. However, for precise solutions, you might need to use a graphing calculator or software.

🌟 Note: While graphing provides visual insight, it might not be precise enough for decimal or non-integer solutions.

Matrix Method

The matrix method involves:

1. Setting up a matrix with coefficients and constants.
2. Using Gaussian elimination to create an echelon form.
3. Back-substituting to solve.

Here’s how you might use the matrix method for the example:

1. Multiply row 1 by 1/2 to make the first element 1.
2. Subtract row 1 from row 2 to zero out the x coefficient in the second row.
3. Row reduce to get the solution.

🛠️ Note: The matrix method is powerful but requires understanding matrix operations, which can be daunting for beginners.

Key Takeaways

By now, you're familiar with the primary methods for solving systems of equations. Here are key points to remember:

• Choose the method that suits the given equations or your comfort level with calculations.
• Substitution and elimination are straightforward for linear systems.
• Graphing provides visual solutions but might lack precision.
• The matrix method offers systematic solutions, especially useful for larger systems or in computer science applications.

Practice is the key to mastering these techniques. Try solving different types of systems, from linear to nonlinear, to gain a comprehensive understanding. Remember, each method has its unique advantages, and choosing the right one can make problem-solving much easier.

What are the advantages of the elimination method over substitution?

+

The elimination method can be more straightforward when dealing with systems where variables are easily aligned with each other for elimination. It might require fewer calculations and is often quicker for systems with multiple variables or where substitution would lead to complex expressions.

How do I know if a system of equations has infinitely many solutions?

+

If the equations are multiples of each other or if graphing reveals lines that overlap perfectly, the system has infinitely many solutions. This indicates dependency where one equation can be derived from another, resulting in the same line or curve.

Is there a method that’s better for all types of systems of equations?

+

No single method is universally better; the efficiency depends on the specific system of equations. Substitution works well when one variable is isolated, elimination is effective when equations can be quickly aligned, graphing is good for visualization, and matrix methods are comprehensive for any system but require more learning.