Master Trigonometry with our Trig Ratios Practice Worksheet

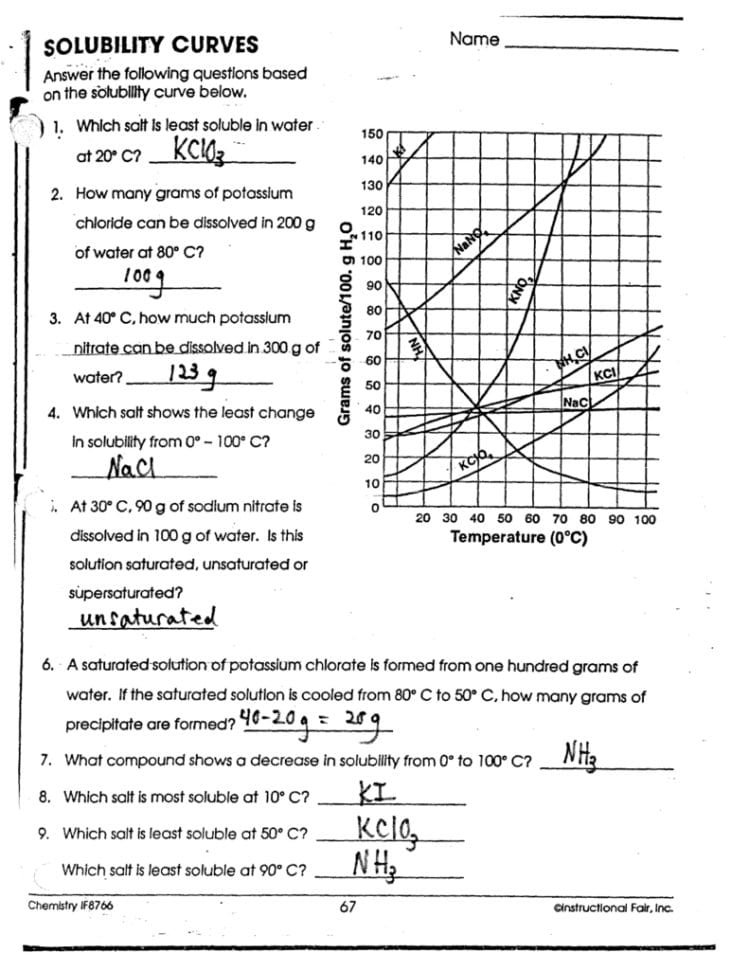
Mastering trigonometry can be a rewarding journey, opening up new dimensions in math, science, and even in everyday problem-solving. Trigonometry ratios lie at the heart of this study, forming the bedrock upon which complex trigonometric principles are built. In this comprehensive guide, we delve into the essentials of trigonometry ratios and provide you with a Trig Ratios Practice Worksheet to solidify your understanding. Whether you're a high school student preparing for a test, an enthusiast looking to refresh your knowledge, or someone keen on exploring trigonometry's real-world applications, this post is designed to enhance your learning experience.
Understanding Trig Ratios

Trigonometry, at its core, involves the study of triangles, particularly right triangles. The primary trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). These ratios are defined in relation to a right triangle where:
- Sine (sin): This ratio is the length of the side opposite to the angle divided by the hypotenuse. In mathematical terms, sin θ = opposite/hypotenuse.
- Cosine (cos): The cosine ratio takes the length of the side adjacent to the angle and divides it by the hypotenuse. Hence, cos θ = adjacent/hypotenuse.
- Tangent (tan): Tangent compares the length of the side opposite the angle to the side adjacent to it. Therefore, tan θ = opposite/adjacent.
🌟 Note: When dealing with angles beyond 90 degrees or negative angles, trigonometric values can be found using periodic identities or by extending the right triangle into the unit circle.
Trig Ratios Practice Worksheet

The practice of trigonometric ratios is fundamental for mastering trigonometry. Here is a worksheet designed to test and improve your proficiency:
| Question | Answer |
|---|---|
| If θ = 30 degrees, find sin(θ). | 0.5 |
| What is the value of cos(60 degrees)? | 0.5 |
| Find tan(45 degrees). | 1 |
| Given a right triangle where the opposite side to θ is 4 and the hypotenuse is 5, find sin(θ). | 0.8 |
| A triangle has an adjacent side of 3 and a hypotenuse of 5, calculate cos(θ). | 0.6 |

🔍 Note: Remember to use the Pythagorean theorem to find unknown sides if necessary. For example, if you only have one side of the triangle given, you might need to solve for the other sides before applying the trigonometric ratios.
Practical Applications of Trigonometry Ratios

Understanding trigonometric ratios extends beyond classroom problems; they are integral in many real-world scenarios:
- Navigation and Mapping: Pilots and sailors use trigonometry to determine their bearings and locations on maps.
- Construction and Architecture: Calculating heights of buildings, angles of elevation or depression, and even roof pitches all involve trigonometry.
- Physics and Engineering: From analyzing force vectors to calculating trajectories, trigonometric principles help solve complex problems.
- Computer Graphics: Trigonometry is crucial for rendering 3D scenes, creating animations, and modeling rotations in games and simulations.
Steps to Solve Trigonometric Problems

Here's a structured approach to solving trigonometric problems:
- Identify the Right Triangle: Understand which angles and sides you are dealing with.
- Determine What You Need: Decide if you need sine, cosine, or tangent based on the sides you have and need to find.
- Apply the Ratio: Use the relevant trigonometric ratio to calculate the angle or length you're solving for.
- Use Inverse Functions: If you're looking for the angle, use inverse trigonometric functions (arcsin, arccos, arctan).
- Check Your Work: Verify your calculations to ensure accuracy, especially for multi-step problems.
💡 Note: When using calculators, ensure your device is set to the correct angle mode (degrees or radians) for accurate results.
In concluding our journey through trigonometry ratios, it's clear that these fundamental principles not only enrich your understanding of mathematics but also provide practical tools for solving problems in various fields. By practicing with the Trig Ratios Worksheet, you've taken a step towards mastering these essential ratios, ensuring you're equipped to tackle more complex trigonometric problems or real-life scenarios where trigonometry is key.
How do you remember the trigonometric ratios?

+
A common mnemonic to remember the trigonometric ratios is SOHCAHTOA - Sine is Opposite over Hypotenuse, Cosine is Adjacent over Hypotenuse, and Tangent is Opposite over Adjacent.
Can trigonometry ratios be negative?
+
Yes, when angles are considered in the unit circle or in reference to coordinate axes, trigonometric functions can yield negative values depending on which quadrant the angle lies in.
How are trigonometric ratios used in non-right triangles?

+
For non-right triangles, you can use the Law of Sines or the Law of Cosines, which are extensions of the basic trigonometric ratios to handle oblique angles and sides.