Unlock the Mystery of Triangles: Pythagorean Theorem Worksheet Key
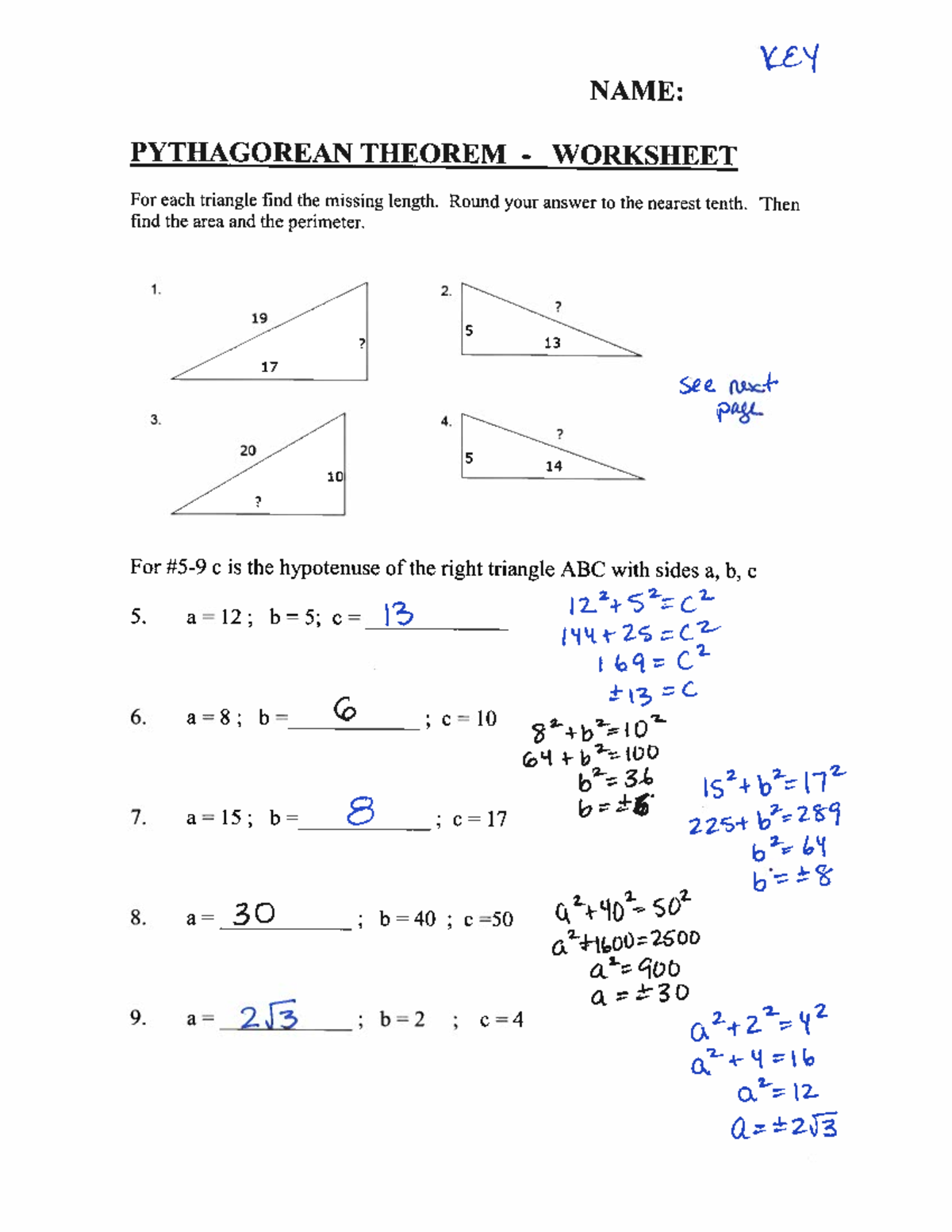
Delving into the world of geometry, particularly triangles, opens up a realm of fascinating concepts and principles. One such cornerstone principle that has both intrigued and baffled students for generations is the Pythagorean Theorem. This theorem not only serves as a bridge to understand the relationship between the sides of a right-angled triangle but also plays an essential role in various fields from architecture to physics, and even art. In this comprehensive guide, we'll unlock the mystery behind the Pythagorean Theorem, explore its application through worksheets, and provide you with keys to ensure you master this fundamental concept with ease.
What is the Pythagorean Theorem?

The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of squares of the other two sides. Symbolically, if a and b are the lengths of the legs, and c is the hypotenuse, the theorem is formulated as:
a² + b² = c²
The Proofs of the Pythagorean Theorem
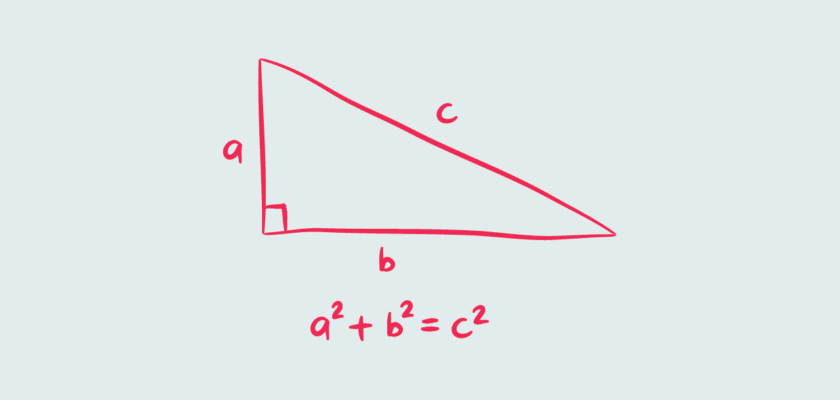
The beauty of the Pythagorean Theorem lies in the multitude of ways it can be proven. Here are some traditional proofs:
- Geometric Proof: One can physically rearrange the squares on the sides of the triangle to form a larger square with an area equal to c².
- Algebraic Proof: Using algebraic manipulation, you can derive the theorem through equations like expanding (a+b)² - 4ab/2.
Application of Pythagorean Theorem in Real Life

The Pythagorean Theorem isn't just confined to textbooks; it has numerous real-world applications:
- Architecture and Construction: To ensure buildings and structures are perfectly square and level.
- Surveying: For determining distances without direct measurement.
- Video Games: To calculate diagonal distances and line-of-sight in 3D environments.
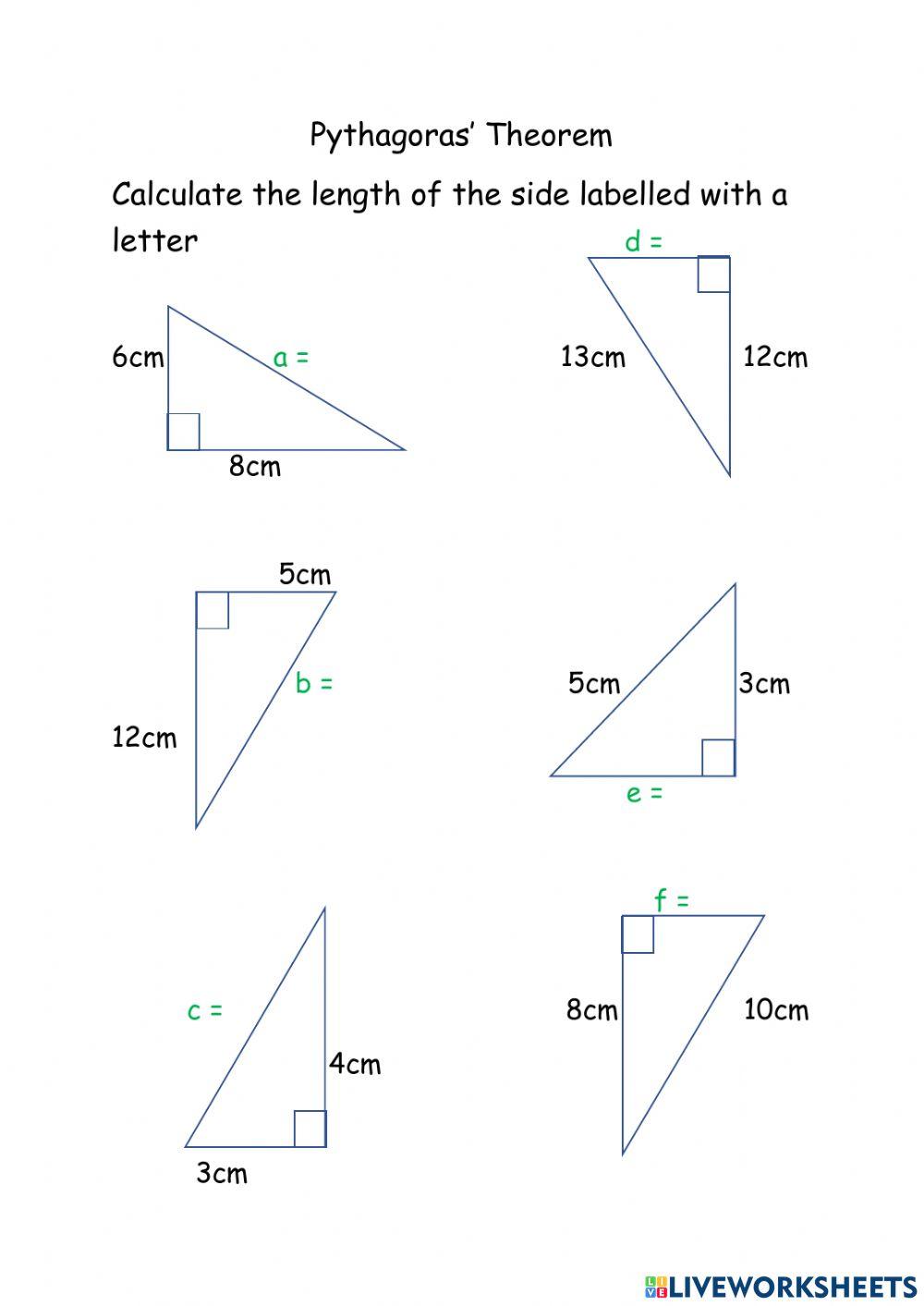
Pythagorean Theorem Worksheets and Key
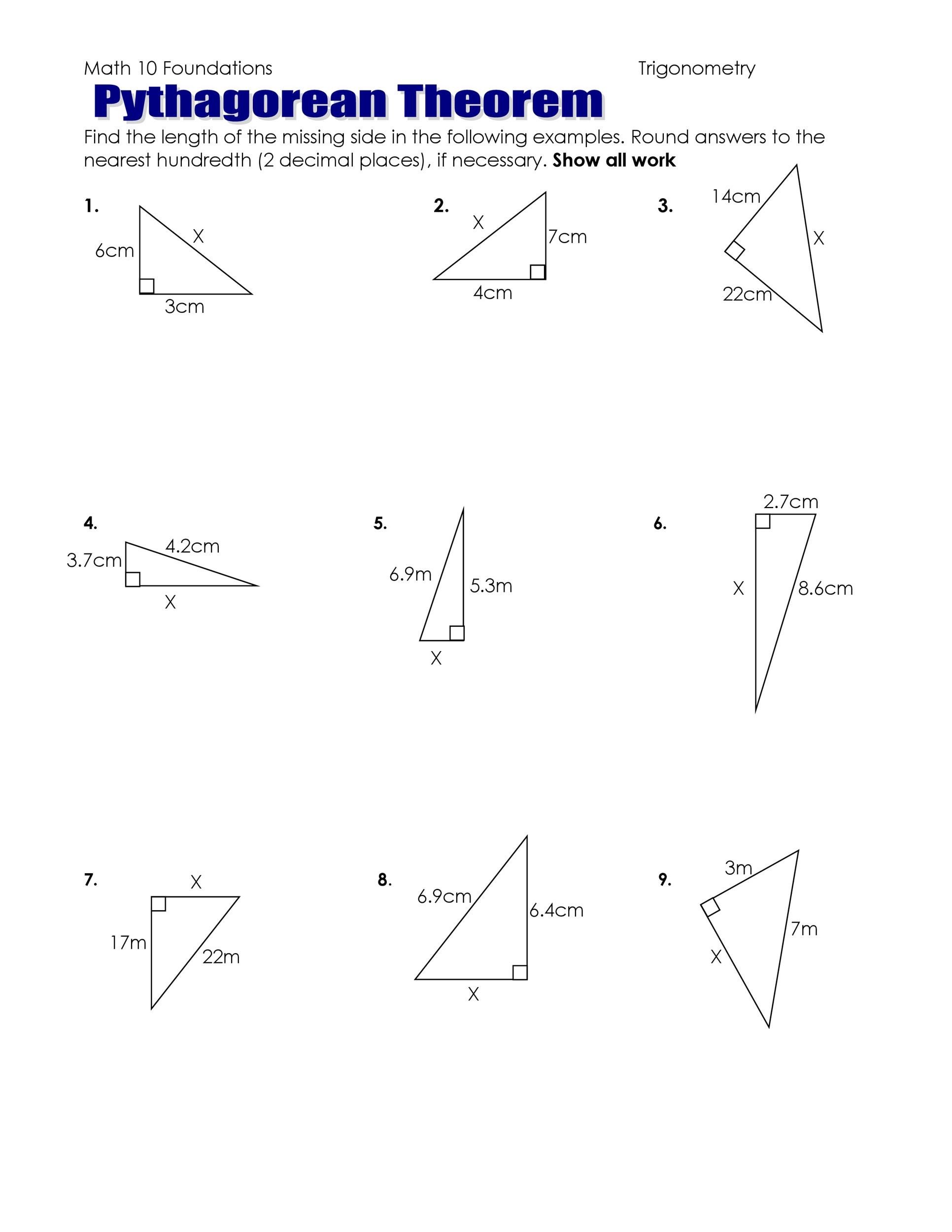
To master the Pythagorean Theorem, one needs practical experience through worksheets. Here's how you can approach such exercises:
Worksheet Examples:

| Problem | Solution |
|---|---|
| Find the length of the hypotenuse if the legs are 3 units and 4 units. | a = 3, b = 4 3² + 4² = c² 9 + 16 = c² c² = 25 c = √25 = 5 |
| Determine the length of one leg when the hypotenuse is 10 units and one leg is 6 units. | a = 6, c = 10 a² + b² = c² 6² + b² = 10² 36 + b² = 100 b² = 100 - 36 b² = 64 b = √64 = 8 |

📝 Note: When solving these problems, it's essential to label and keep track of the known and unknown variables clearly to avoid confusion.
FAQs on Pythagorean Theorem

Why do we need to square the sides in the Pythagorean Theorem?
+
The squaring of the sides allows for a proportional relationship that holds true regardless of the sizes of the triangles involved, making the theorem universally applicable to all right-angled triangles.
Can the Pythagorean Theorem be used on non-right triangles?

+
The Pythagorean Theorem applies specifically to right-angled triangles. For non-right triangles, other theorems like the Law of Cosines would be used to relate the sides.
What are some real-life examples where understanding the Pythagorean Theorem is useful?
+
It's used in navigation (like GPS calculations), creating designs where square or rectangular spaces are involved, and even in ensuring level foundations in construction.
Through this exploration, we’ve uncovered the elegance of the Pythagorean Theorem, not just as a mathematical equation, but as a fundamental principle that touches many aspects of our daily lives. From solving problems on worksheets to understanding its practical implications, we’ve seen how this theorem connects geometry to real-world applications, enhancing our appreciation for its depth and utility. Remember, every journey in mathematics begins with understanding and applying these basic concepts, empowering us to tackle more complex challenges with confidence and curiosity.



