5 Easy Steps to Master Wavelength Calculations

Whether you are a student grappling with the fundamentals of wave mechanics, a hobbyist exploring the science behind light and sound, or a professional calibrating your equipment, understanding how to calculate wavelength can be fundamental to your field. Wavelength, denoted by the Greek letter lambda (λ), plays a crucial role in how energy travels through mediums, how colors are perceived, or how sound waves produce music or noise. This guide will walk you through the five essential steps to master wavelength calculations effectively and easily.
Understanding the Basics

Before diving into the calculations, let’s cover some basic principles:
- Wavelength (λ): The distance over which the wave’s shape repeats, measured in meters.
- Frequency (f): The number of waves passing a point in one second, measured in Hertz (Hz).
- Speed of Wave (v): This depends on the medium the wave travels through; for light in a vacuum, it’s approximately 299,792,458 meters per second.
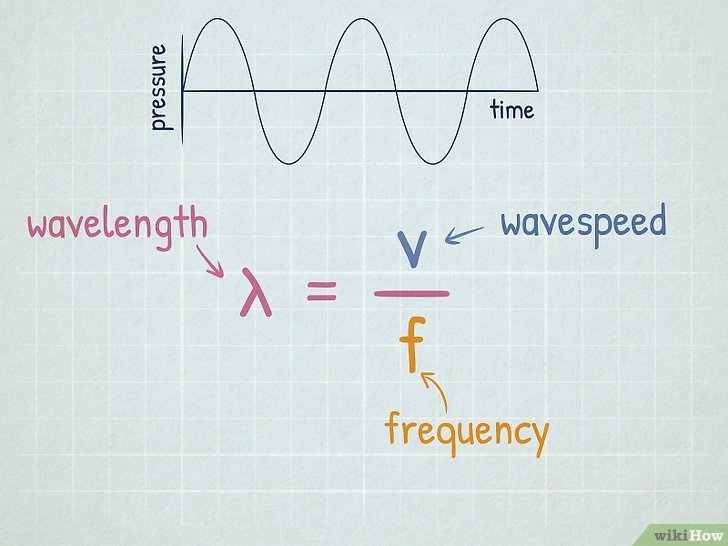
🚀 Note: Remember, for electromagnetic waves in a vacuum, the speed is constant, and the relationship between wavelength, frequency, and speed is given by the formula \lambda = \frac{v}{f} .
Step 1: Identify the Given Quantities

To calculate wavelength, you must first know:
- The speed of the wave (v)
- The frequency (f)
In some problems, you might be given the period (T), which is the time taken for one complete cycle of the wave, and can be used to find frequency through the relationship f = \frac{1}{T} .
Step 2: Apply the Wavelength Formula

With the variables known, apply the basic formula:
λ = v / fHere's an example:
If light travels at a speed of 3 \times 10^8 meters per second (m/s) in a vacuum, and its frequency is 5 \times 10^{14} Hz, the wavelength would be:
λ = (3 x 10^8 m/s) / (5 x 10^14 Hz) = 6 \times 10^-7 m or 600 nm⚠️ Note: Units must be consistent for the formula to yield correct results; always convert your units to base SI units (meters, seconds) before calculations.
Step 3: Solve for Frequency or Speed

Should you be missing frequency or speed, you’ll need to find them:
- Frequency: If you have the period, use ( f = \frac{1}{T} ).
- Speed: If you have wavelength and frequency, rearrange the formula to ( v = \lambda \times f ).
Step 4: Understand Medium Effects
The speed of a wave can change when it moves through different mediums:
- Light slows down in denser mediums, affecting its wavelength.
- Sound changes speed based on density, temperature, and elasticity of the medium.
A practical example:
| Medium | Speed of Light (m/s) |
|---|---|
| Vacuum | 299,792,458 |
| Water | 225,000,000 |

Calculating the wavelength in water using the frequency from above:
λ = (225,000,000 m/s) / (5 x 10^14 Hz) = 4.5 \times 10^-7 m or 450 nmStep 5: Practice and Application

The best way to master wavelength calculations is through:
- Solving numerous problems to internalize the formulas and units.
- Applying wavelength calculations to real-world situations like selecting antennae for different frequency bands, understanding acoustics, or choosing optical filters for light wave experiments.
To conclude, mastering wavelength calculations involves understanding the core concepts, applying the correct formulas, and being mindful of how the medium influences wave behavior. With practice, you'll find these calculations become second nature, allowing you to explore and manipulate waves in various scientific and technological contexts effectively.
Why is the speed of light in a vacuum constant?

+
The speed of light in a vacuum is a universal constant because it forms the foundation of relativity and electromagnetism. This constancy is a fundamental property of our universe, established through countless experimental verifications.
How does changing the medium affect wavelength?

+
When a wave enters a denser medium, its speed decreases, which directly impacts the wavelength. As the frequency remains constant, the wavelength adjusts to maintain the wave’s energy propagation through the medium.
Can I calculate wavelength if I only have the period?

+
Yes, by converting the period to frequency with ( f = \frac{1}{T} ), you can then use the standard wavelength formula to calculate the wavelength.
How do I account for the wavelength of light in materials other than a vacuum?
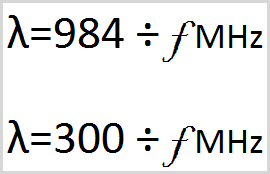
+
Use the index of refraction of the medium. Light speed in the medium can be calculated as ( v = \frac{c}{n} ), where ( n ) is the refractive index, and ( c ) is the speed of light in a vacuum.
What are practical applications of wavelength calculations?

+
Wavelength calculations are crucial in designing antenna systems, understanding acoustic properties, calibrating scientific instruments, and in fields like spectroscopy, optics, and telecommunications.