Master the Sum of Interior Angles of Polygons Easily
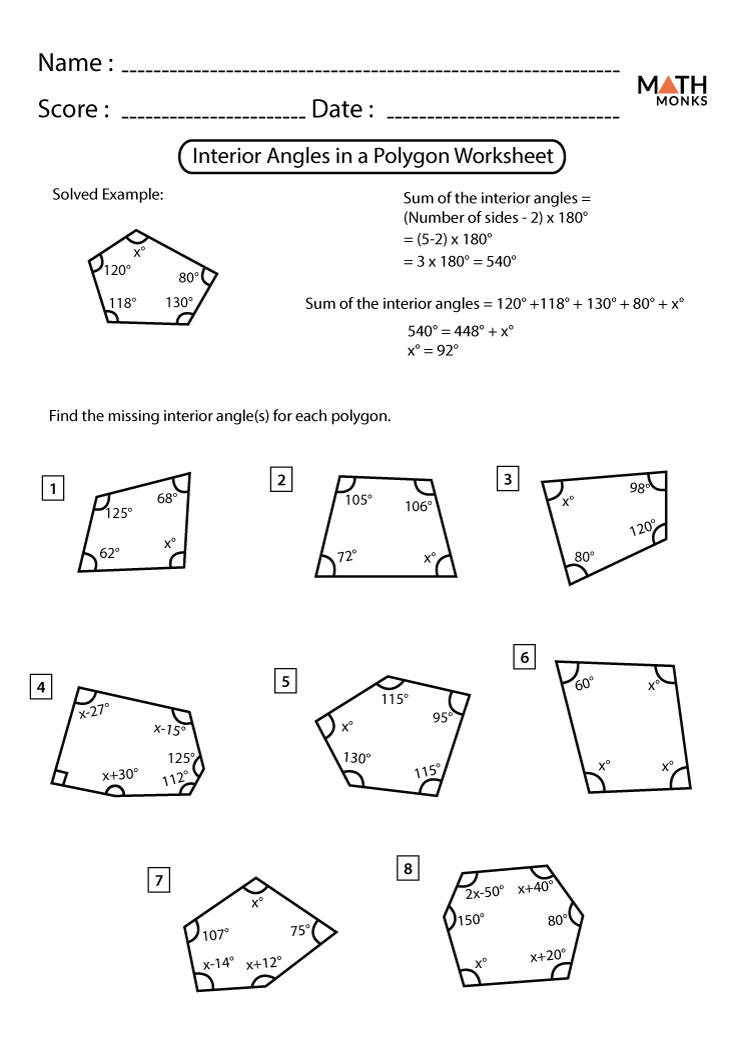
Understanding the sum of the interior angles of polygons is fundamental in geometry, serving as a cornerstone for numerous theorems and applications. Whether you're a student diving into the world of shapes or a professional revisiting geometry, mastering this concept can simplify many geometric problems. Let's explore how to calculate the sum of interior angles of polygons effectively.
Why Know the Sum of Interior Angles?
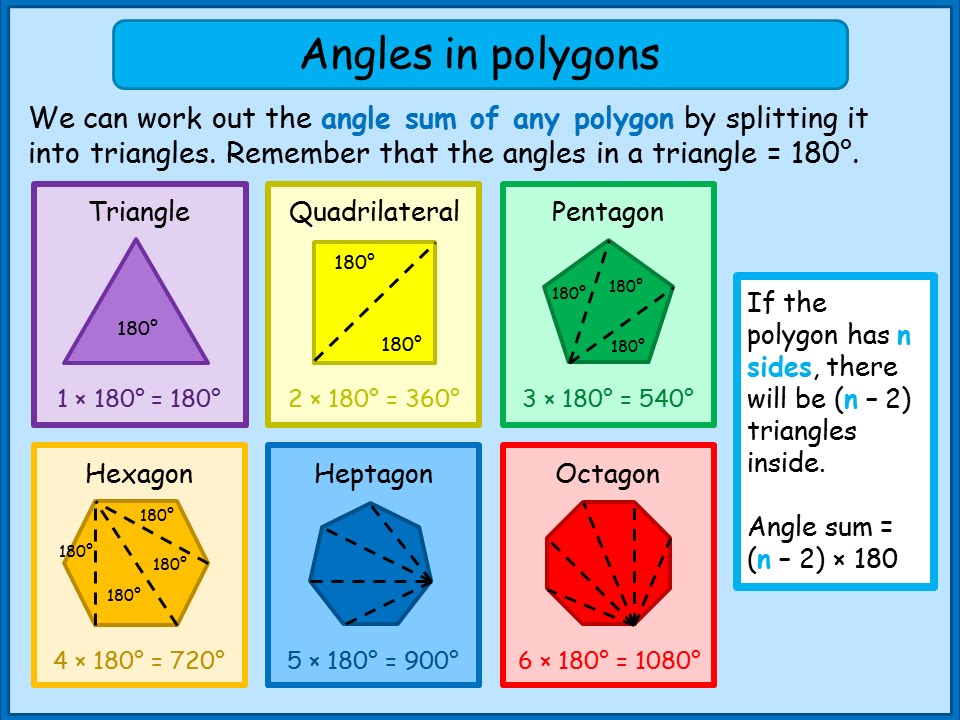
Knowing the sum of interior angles helps in:
- Identifying and classifying polygons
- Solving geometric problems involving angles
- Understanding the properties and relationships in polygons
Understanding the Basics
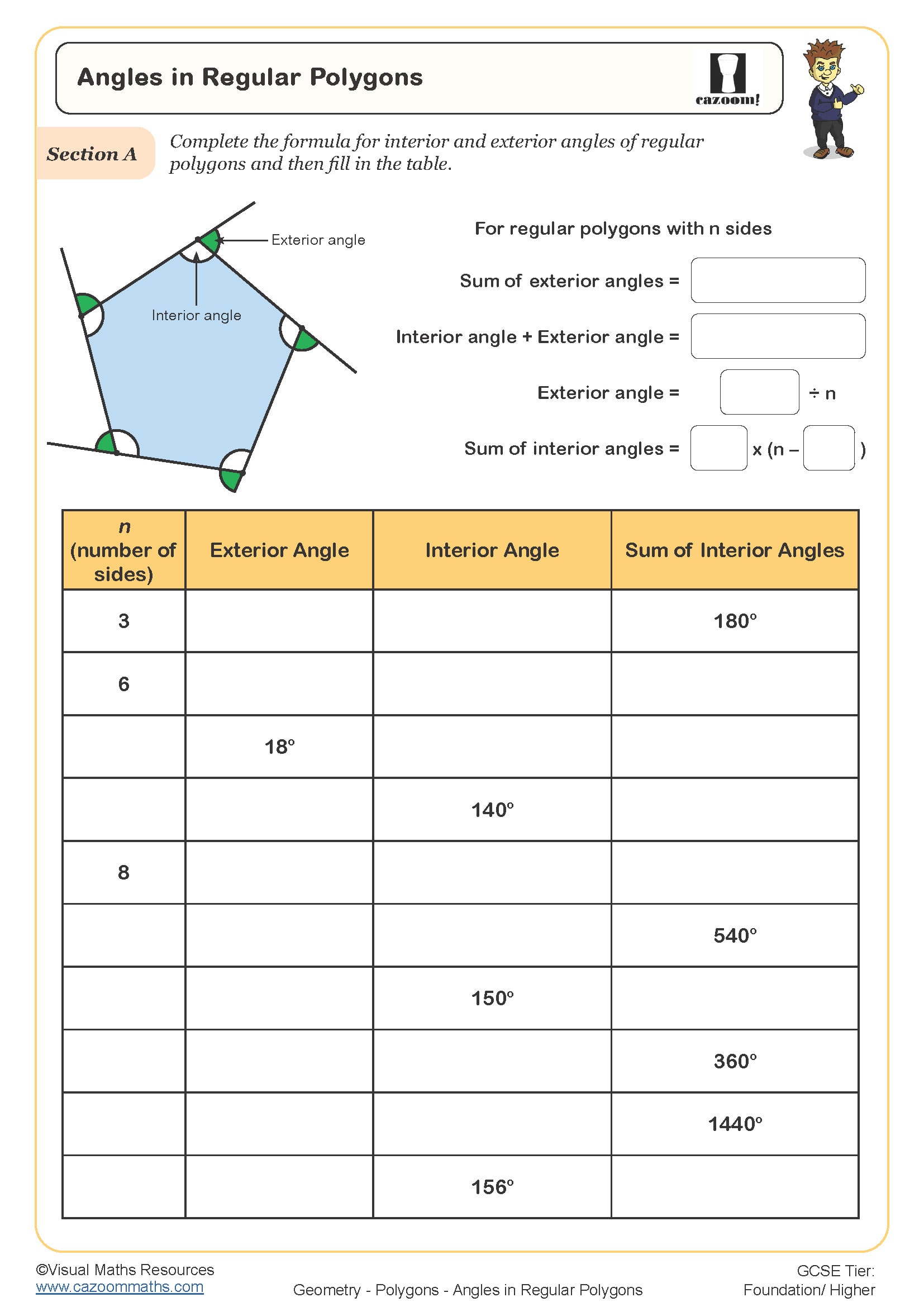
Each polygon, whether it’s a simple triangle or a complex dodecagon, has a unique sum of interior angles. Here’s a brief overview of what we need to know:
- Interior angles are the angles inside the polygon at each of its vertices.
- Regular polygons have all sides and angles equal.
- Any polygon with n sides can be dissected into n - 2 triangles by drawing diagonals from one vertex to all non-adjacent vertices.

Sum of Interior Angles Formula

The formula to find the sum of the interior angles of a polygon with n sides is:
(n - 2) * 180°🔍 Note: This formula works for any polygon, regardless of whether it is regular or not.
Step-by-Step Examples

To solidify your understanding, let’s calculate the sum of interior angles for a few common polygons:
Example: Triangle
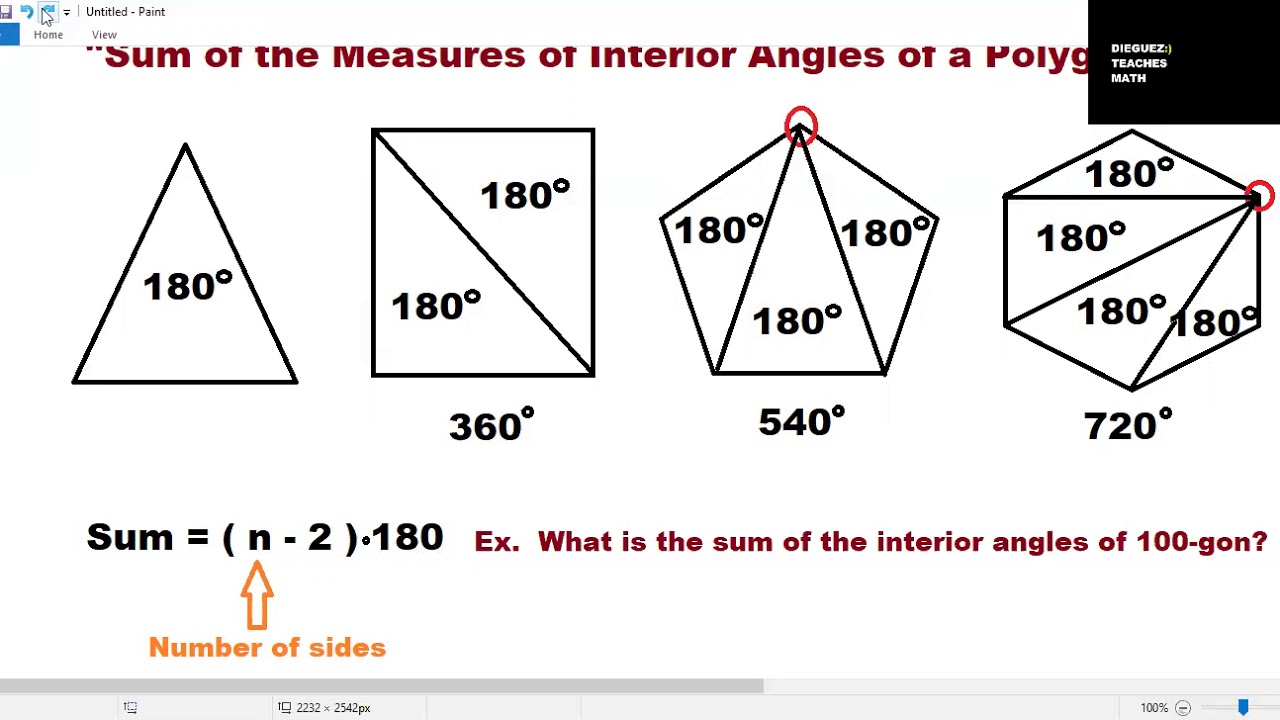
A triangle has 3 sides. Using our formula:
(3 - 2) * 180° = 180°Example: Pentagon

A pentagon has 5 sides:
(5 - 2) * 180° = 540°
Example: Nonagon

With 9 sides, the sum of the interior angles for a nonagon is:
(9 - 2) * 180° = 1260°🔍 Note: The sum of interior angles increases as the number of sides in a polygon increases.
Regular vs. Irregular Polygons

While the formula works universally, here’s how it applies:
- For regular polygons, all interior angles are equal.
- In irregular polygons, the angles are not necessarily equal, but their sum still follows the formula.
| Polygon | Number of Sides (n) | Sum of Interior Angles |
|---|---|---|
| Triangle | 3 | 180° |
| Quadrilateral | 4 | 360° |
| Pentagon | 5 | 540° |

Real-World Applications
Understanding the sum of interior angles isn’t just for academic pursuits. It’s used in:
- Architecture for designing stable structures
- Land surveying for parcel subdivision
- Designing patterns or tiles that fit together perfectly
Summarizing our journey into the sum of interior angles, we've seen how a simple formula can unlock a deep understanding of polygons. Whether it's a triangle or a multifaceted polygon, this concept not only helps in solving geometric problems but also has practical applications in various fields. By internalizing this formula, you're not just learning geometry; you're learning a universal language of shape and structure.
What’s the difference between interior and exterior angles?

+
Interior angles are those inside a polygon at its vertices, while exterior angles are formed outside the polygon by extending one of its sides. For any polygon, the sum of its exterior angles is always 360°.
Can I apply this formula to concave polygons?

+
Yes, the formula for calculating the sum of interior angles applies to all polygons, including concave ones. However, for concave polygons, one or more interior angles might be greater than 180°.
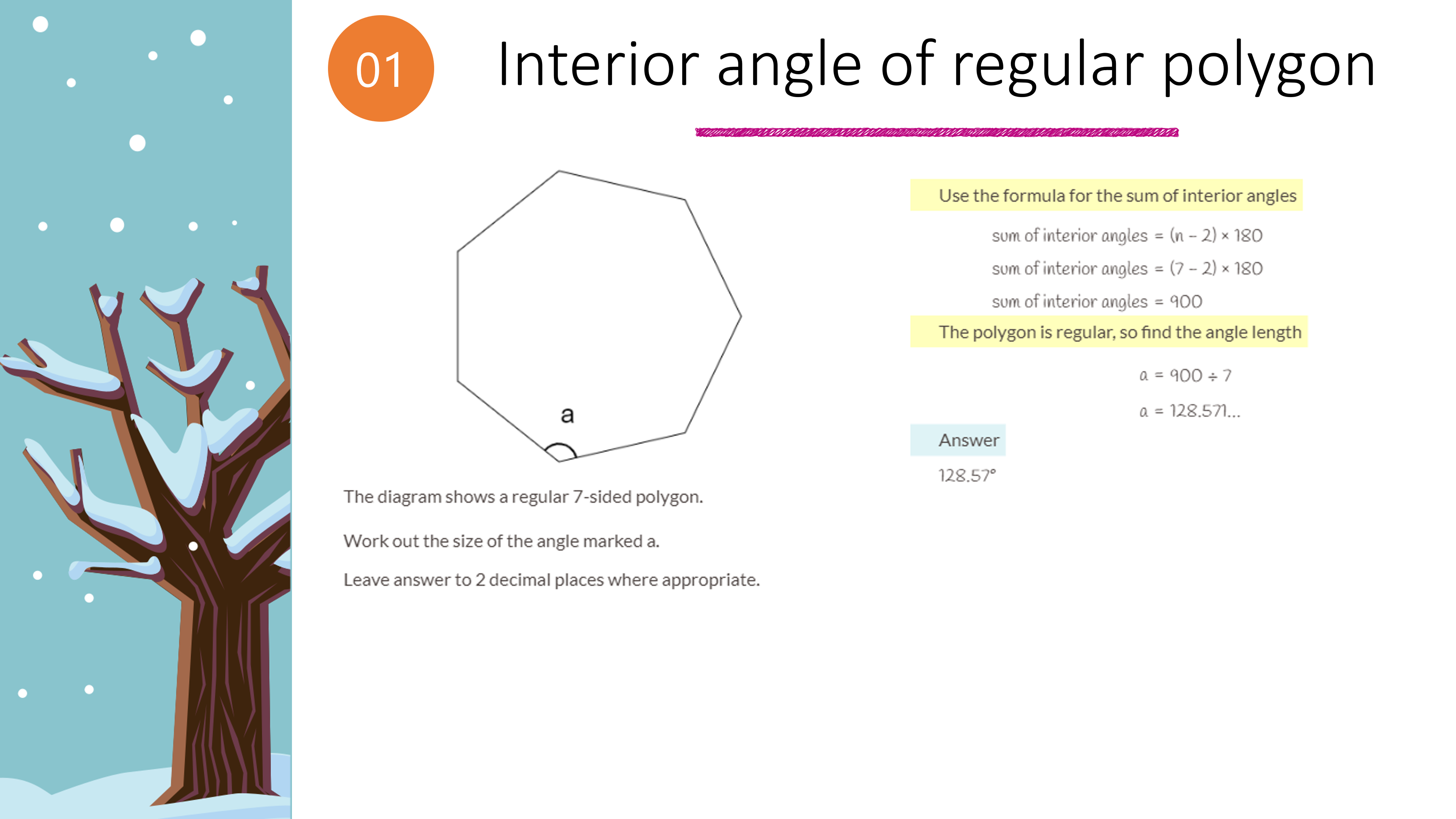
How do I find the measure of each interior angle of a regular polygon?
+
For regular polygons, where all angles are equal, you can divide the sum of interior angles by the number of sides: ((n - 2) * 180°) / n.



