5 Ways to Calculate Area of Different Shapes Easily

In the world of mathematics, one of the most frequent tasks we encounter is calculating the area of various shapes. Whether you're a student, a professional, or someone with a casual interest in numbers and shapes, understanding how to easily calculate the area of different shapes is both useful and empowering. This blog post will guide you through five common shapes and provide straightforward methods to determine their areas, ensuring you have the tools to tackle these calculations effortlessly.
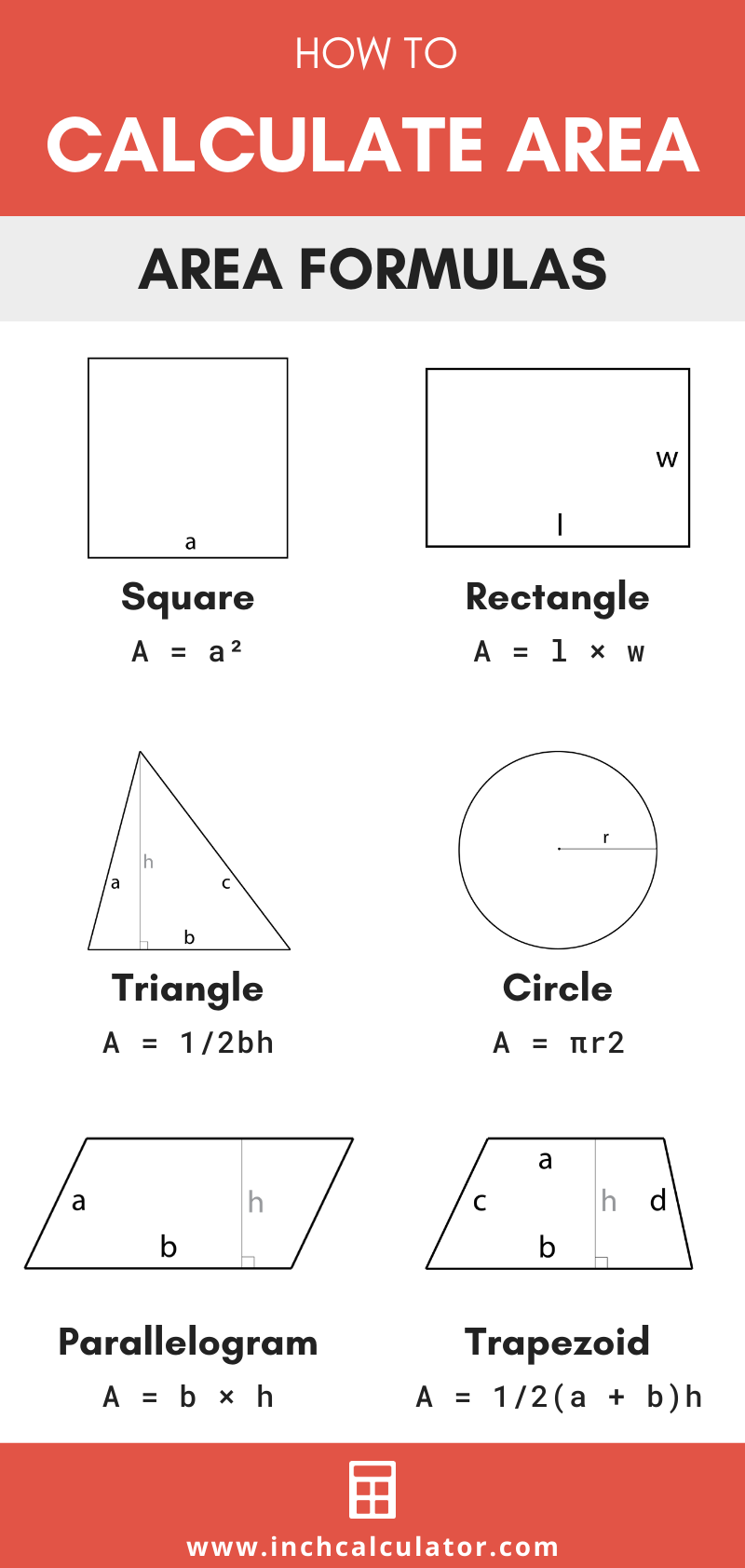
Rectangle


The rectangle is perhaps the simplest shape to calculate the area of:
- Formula: Area = Length × Width
- Example: If your rectangle has a length of 5 units and a width of 3 units, the area is calculated as:
| Length | Width | Area |
| 5 | 3 | 15 |
💡 Note: If the rectangle is also a square, then the formula simplifies to Area = Side × Side.
Triangle


Triangles, while diverse in their types, share a simple formula for area:
- Formula: Area = (Base × Height) / 2
- Example: For a triangle with a base of 10 units and a height of 6 units:
| Base | Height | Area |
| 10 | 6 | 30 |
Remember, for right triangles, the base and height are the two sides adjacent to the right angle.
Circle
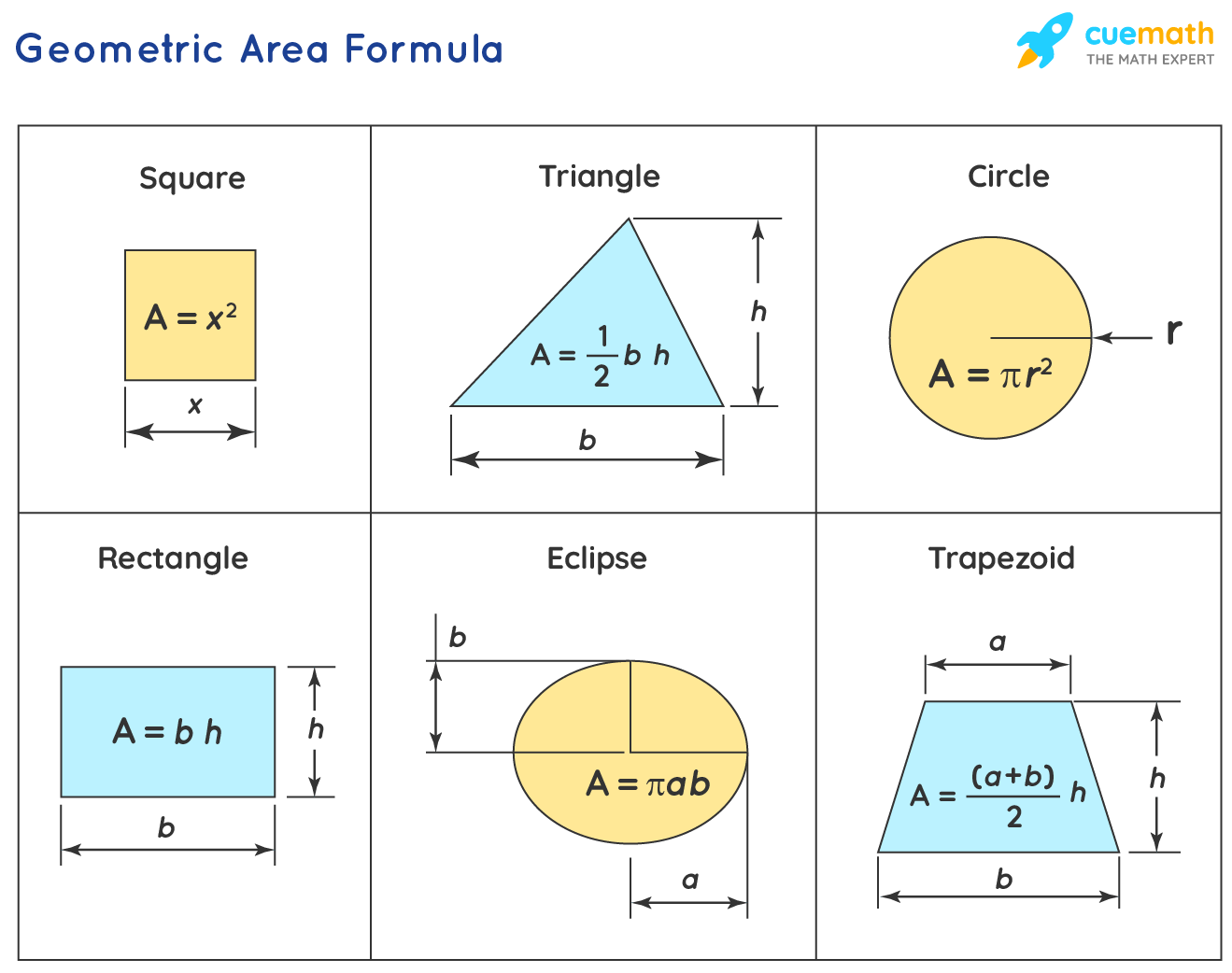

To calculate the area of a circle, we introduce a constant:
- Formula: Area = πr², where r is the radius of the circle.
- Example: If the radius of a circle is 4 units:
| Radius | π | Area |
| 4 | 3.1416 | 50.27 (approx.) |
💡 Note: Using an accurate value of π will yield more precise results.
Trapezoid


Trapezoids can be trickier, but with a little breakdown, their area calculation is manageable:
- Formula: Area = ((a + b) × h) / 2, where ‘a’ and ‘b’ are the lengths of the parallel sides, and ‘h’ is the height between them.
- Example: With a = 6, b = 8, and h = 5:
| a | b | h | Area |
| 6 | 8 | 5 | 35 |
If you need to derive the height, drop a perpendicular line from one of the non-parallel sides.
Parallelogram


Parallelograms share the same principle as rectangles, but with an angle:
- Formula: Area = Base × Height
- Example: Base = 7 units, Height = 4 units:
| Base | Height | Area |
| 7 | 4 | 28 |
Remember, the height in a parallelogram is measured perpendicularly from the base.
In closing, these five methods simplify the task of calculating areas for common shapes. Whether for geometry class, construction, or just personal interest, understanding these formulas and how to apply them can save you time and boost your mathematical confidence. When you encounter shapes that are not on this list, remember the principles are often similar; breaking down the shape into familiar components can help in calculating their areas as well. Continue exploring the fascinating world of geometry and never cease to wonder at the simplicity and complexity it holds.
What is the most efficient method to calculate the area of irregular shapes?

+
The most efficient method often involves breaking down the irregular shape into simpler geometric figures. For example, a complex polygon could be divided into triangles or rectangles, whose areas are then summed up.
Can I use these formulas in real-life applications?

+
Absolutely. From architecture to landscaping, these formulas are used daily to calculate spaces, materials needed, and more. They are foundational in many practical fields.
Why is the formula for a circle’s area different?

+
The formula for a circle’s area involves π because a circle’s circumference can be thought of as the perimeter of an infinite number of tiny rectangles, each with a height equal to the radius. This integration leads to the familiar πr² formula.