5 Simple Strategies for Solving Equations Easily
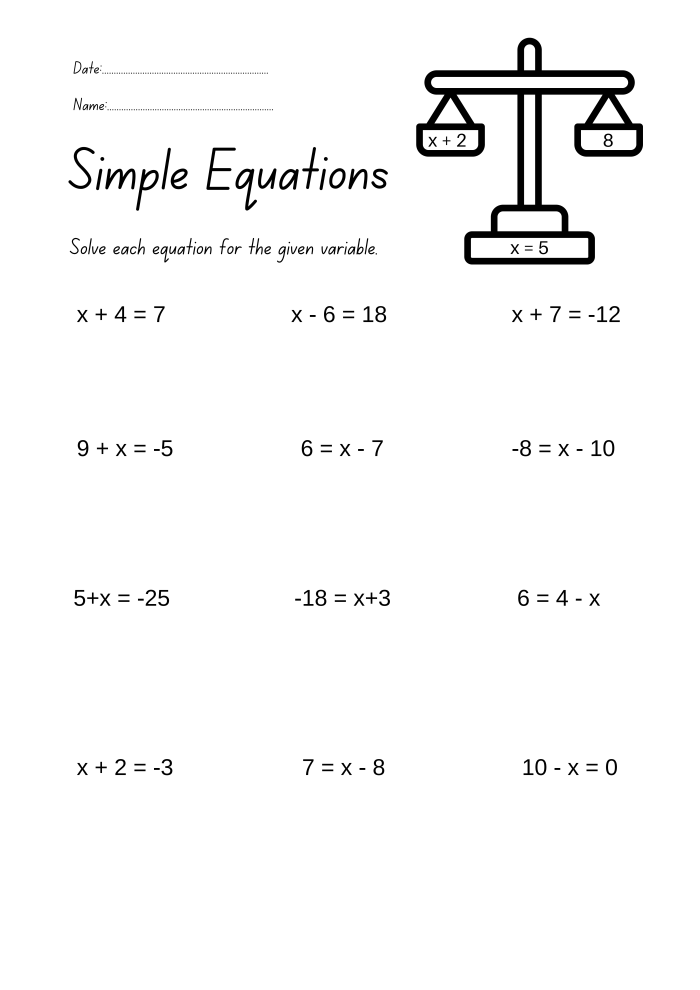
Mathematics can be a challenging subject, but with the right strategies, solving equations becomes an exciting puzzle rather than a daunting task. Whether you're a student struggling with algebra or someone who wants to brush up on their math skills for work or study, understanding how to approach equations methodically can greatly enhance your learning curve and confidence. Let's explore five simple yet effective strategies to solve equations with ease.
1. Understand the Basics

Before diving into complex problem-solving, it's crucial to solidify your understanding of the foundational concepts:
- Equation Structure: Grasp how an equation is set up. Know the difference between variables and constants, what it means for an equation to balance, and the essence of solving equations.
- Operations: Familiarize yourself with basic arithmetic operations (addition, subtraction, multiplication, division) and how they work with equations.
- Terms: Identify like terms, unlike terms, and understand how to combine them or isolate variables.
- Order of Operations: Remember PEMDAS (Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right)) to ensure correct solving.
2. Simplification is Key

The process of simplification is about transforming complex expressions into simpler ones, making it easier to solve the equation. Here’s how you can simplify:
- Combine Like Terms: Group together terms that can be added or subtracted directly. For instance, in the equation 4x + 6 - 2x = 3x + 6, combining like terms gives you 2x + 6.
- Distribute: Use the distributive property to distribute a term to a group of terms inside parentheses. For example, 3(x + 2) = 3x + 6.
- Remove Parentheses: Sometimes equations include parentheses which should be eliminated by performing operations.
- Divide or Multiply: To simplify an equation with fractions, multiply the entire equation by the denominator, or if it's too complex, find a common denominator to work with.
💡 Note: Simplification often makes it easier to isolate the variable, leading to quicker solutions.
3. Isolate the Variable

Isolating the variable is about ensuring that the variable you're solving for stands alone on one side of the equation. Here's the procedure:
- Eliminate Constants: Add or subtract constants to one side of the equation to eliminate them.
- Eliminate Coefficients: Divide or multiply both sides by the coefficient of the variable.
- Move Terms: If there are terms on both sides of the equation, move them so that all terms with the variable are on one side and the constants on the other.
Example:
| Original Equation | Process | Result |
|---|---|---|
| 2x + 3 = 15 | Subtract 3 from both sides | 2x = 12 |
| 2x = 12 | Divide by 2 | x = 6 |

4. Check Your Solution

Once you've solved for the variable, it's wise to double-check your work:
- Substitute the found solution back into the original equation.
- Verify that the equation still balances; if it does, your solution is likely correct.
- If the equation doesn't balance, reassess your steps to find the mistake.
✅ Note: Checking your work reduces the likelihood of miscalculation and confirms the accuracy of your solution.
5. Practice with Different Types of Equations

Being well-rounded in solving various equations will build your confidence and adaptability:
- Linear Equations: Equations like 2x + 5 = 11 which can be solved with basic arithmetic.
- Quadratic Equations: Use the quadratic formula, factoring, or the method of completing the square to solve equations like x^2 + 5x + 6 = 0.
- Systems of Equations: Solve multiple equations simultaneously using substitution or elimination methods.
- Exponential Equations: Transform them into a linear form by using logarithms.
- Inequalities: Similar to solving equations, but results are expressed with symbols like <, >, \leq, \geq.
By regularly practicing with these different types, you'll develop a deeper understanding of when and how to apply the five strategies we've outlined.
Over time, the techniques we've discussed will become second nature. Remember, like any skill, proficiency in solving equations comes with practice and patience. By using these simple yet powerful strategies, you'll not only find solving equations easier but also build a strong foundation in mathematics, which is critical for various fields of study and career paths. Mathematics is more than just numbers; it's a language that opens doors to understanding the universe, its beauty, and complexity.
Why is it important to check the solution after solving?

+
Checking your solution confirms its accuracy and helps catch any errors in your calculation process. It’s a good practice for ensuring mathematical rigor and preventing mistakes that could lead to incorrect conclusions.
How can I simplify more complex equations?
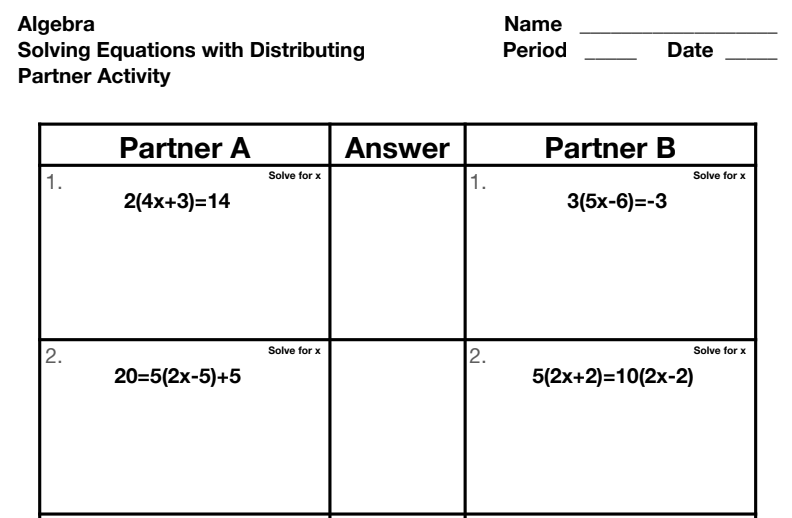
+
To simplify more complex equations, apply the distributive property, combine like terms, eliminate unnecessary constants or coefficients, and use common denominators when dealing with fractions. If the equation still looks complicated, try to factor it out or use substitution to manage multiple variables.
What should I do if I’m stuck on an equation?
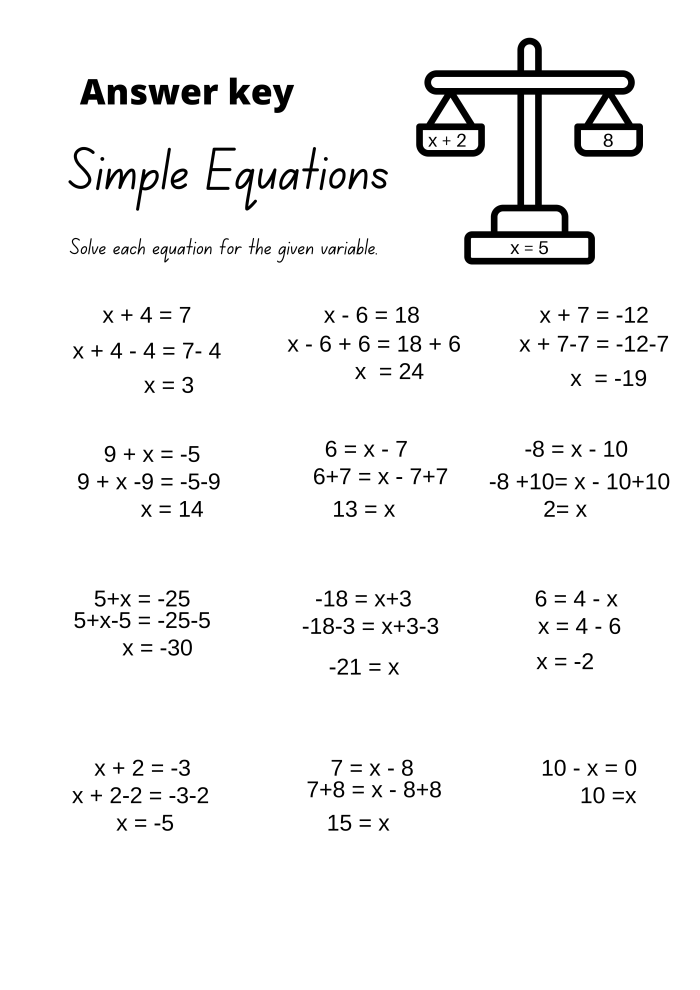
+
If you’re stuck, take a step back and review the equation. Sometimes, sketching the problem or breaking it down into smaller steps can help. Also, make sure you understand the goal of the problem, revisit basic rules, and don’t hesitate to look at similar solved problems for insight.
Related Terms:
- Solving simple equations worksheet pdf



