Mastering Perimeter and Area: Composite Figures Worksheet

Welcome to our comprehensive guide on mastering the calculation of perimeter and area for composite figures. This worksheet is designed to equip students, educators, and math enthusiasts with the skills needed to solve complex geometric problems efficiently. Whether you're preparing for an exam or simply looking to refine your understanding, this guide will walk you through the intricacies of composite shapes, offering step-by-step explanations, examples, and valuable tips for mastering these concepts.

Understanding Composite Figures

Composite figures are geometric shapes composed of two or more simple geometric shapes such as squares, rectangles, triangles, circles, or semicircles. These shapes often appear in real-life scenarios, making the understanding of their perimeter and area an essential skill for everyday problems, engineering, architecture, and more.

Basic Components of Composite Figures

• Squares: A quadrilateral with all sides equal.
• Rectangles: A quadrilateral where opposite sides are equal and all angles are right angles.
• Triangles: Three-sided polygons, which can be equilateral, isosceles, or scalene.
• Circles: A round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the center).
• Semicircles: Half of a circle.

Calculating Perimeter of Composite Figures

Calculating the perimeter of a composite figure involves:

• Identifying the simple shapes that make up the composite figure.
• Finding the perimeter of each individual shape.
• Adding the perimeters of all shapes but ensuring to subtract any internal boundaries that are shared between shapes to avoid double counting.

Here is an example:

To find the perimeter:

1. Label each component: Here, we have a rectangle and a semicircle.
2. Calculate the perimeter of the rectangle:
• Perimeter of rectangle = 2(l + w), where l is length and w is width.
• If l = 12 cm, and w = 5 cm, then the perimeter is 2(12 + 5) = 34 cm.
3. Calculate the circumference of the semicircle (half of the circle):
• Circumference of the full circle = 2πr, where r is the radius of the semicircle.
• If r = 5 cm, then circumference is 2π(5) = 10π. Half of this is 5π.
4. Add the two perimeters but subtract the straight line between rectangle and semicircle:
• Total perimeter = 34 cm + 5π cm - 5 cm (shared side) = 29 + 5π cm.

⚠️ Note: Always consider the arrangement of figures; shared boundaries should only be counted once in perimeter calculations.

Calculating Area of Composite Figures

To calculate the area of composite figures:

• Calculate the area of each individual shape.
• Add these areas together to get the total area of the composite figure.

Continuing with our previous example:

1. Area of the rectangle: A = length × width = 12 cm × 5 cm = 60 cm².
2. Area of the semicircle: A = ½πr² = ½π(5)² = 12.5π cm².
3. Total Area = 60 cm² + 12.5π cm².

📘 Note: When dealing with composite figures that overlap, ensure to subtract the area of overlap if not needed.

Advanced Techniques for Problem Solving

Decomposition and Recomposition

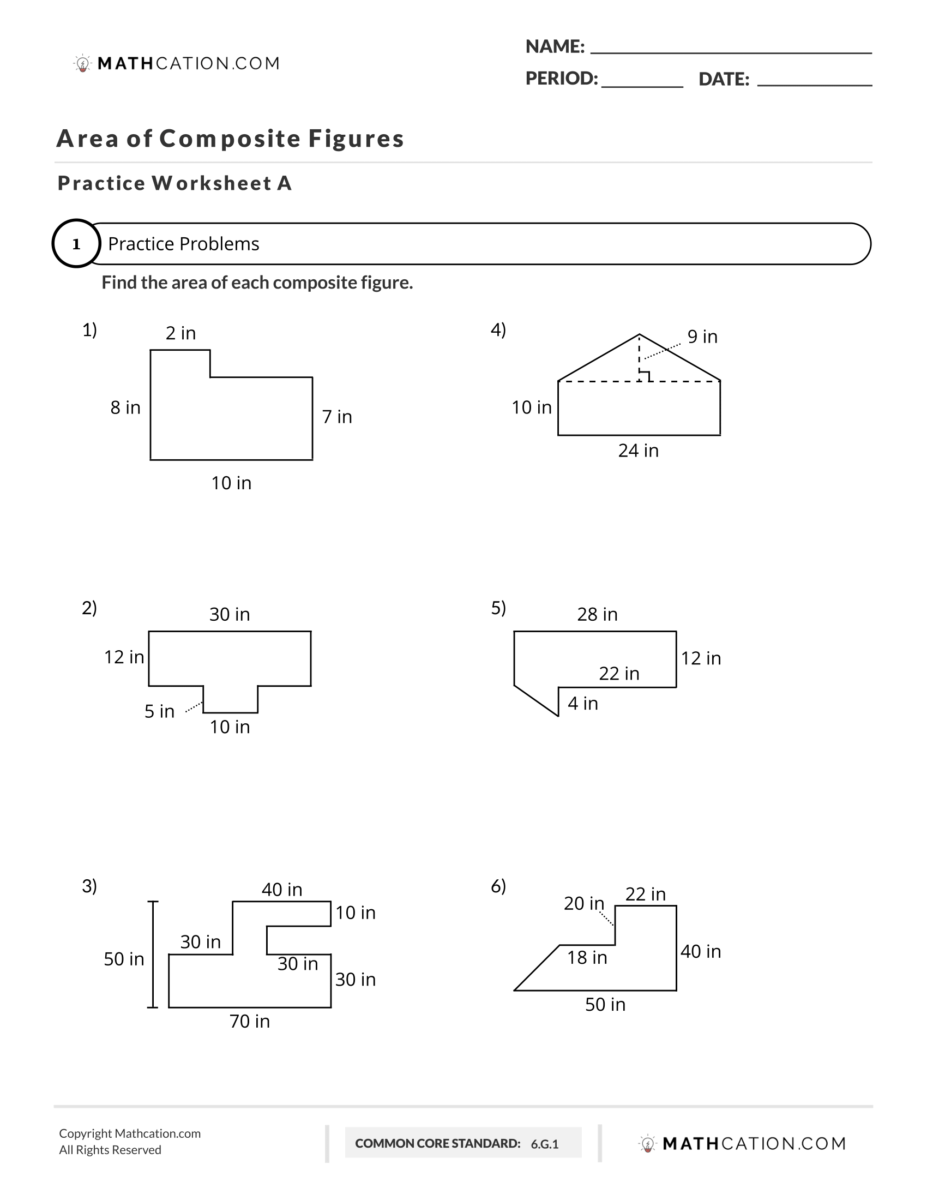
Sometimes, decomposing or recomposing shapes can simplify calculations. For instance, you can:

• Divide a shape into smaller, more manageable parts.
• Add extra shapes temporarily to transform the figure into a more familiar composite shape.

Formulas and Tricks

Here are some useful tricks:

• Heron's Formula: Useful for finding the area of triangles when only the length of the sides are given.
• Circle Sector and Segment Area: Know how to calculate the area of different parts of circles beyond just the semicircle.
• Using Pythagorean Theorem: To find diagonal or sides when shapes are connected at odd angles.

🔹 Note: Understanding and applying these advanced formulas can significantly reduce computation time and complexity in problem-solving.

In conclusion, mastering the calculation of perimeter and area for composite figures is not just about understanding basic geometry but also about applying strategic thinking and problem-solving skills. By breaking down complex shapes into their fundamental components, applying the right formulas, and remembering to account for shared boundaries, you can tackle any composite figure with confidence. These skills not only enhance your mathematical proficiency but are also incredibly practical for real-life applications, from measuring materials for home improvement projects to solving problems in various technical fields.

What are some common mistakes when calculating perimeter of composite figures?

+

Common mistakes include forgetting to subtract the shared boundaries between shapes, incorrectly accounting for the circumference of circular sections, or miscalculating the perimeter due to visual interpretation errors.

How can one quickly identify which basic shapes make up a composite figure?

+

Practice identifying basic shapes by looking for straight lines, right angles, and familiar patterns like equilateral triangles or circles. Also, look for symmetry or any recognizable geometric features that can help you determine the components.

Why do we subtract the shared boundaries when calculating the perimeter of composite figures?

+

Shared boundaries are lines that act as a boundary for two shapes within the composite figure. Counting them twice would inflate the total perimeter. Hence, we subtract these lengths to ensure accurate measurements.