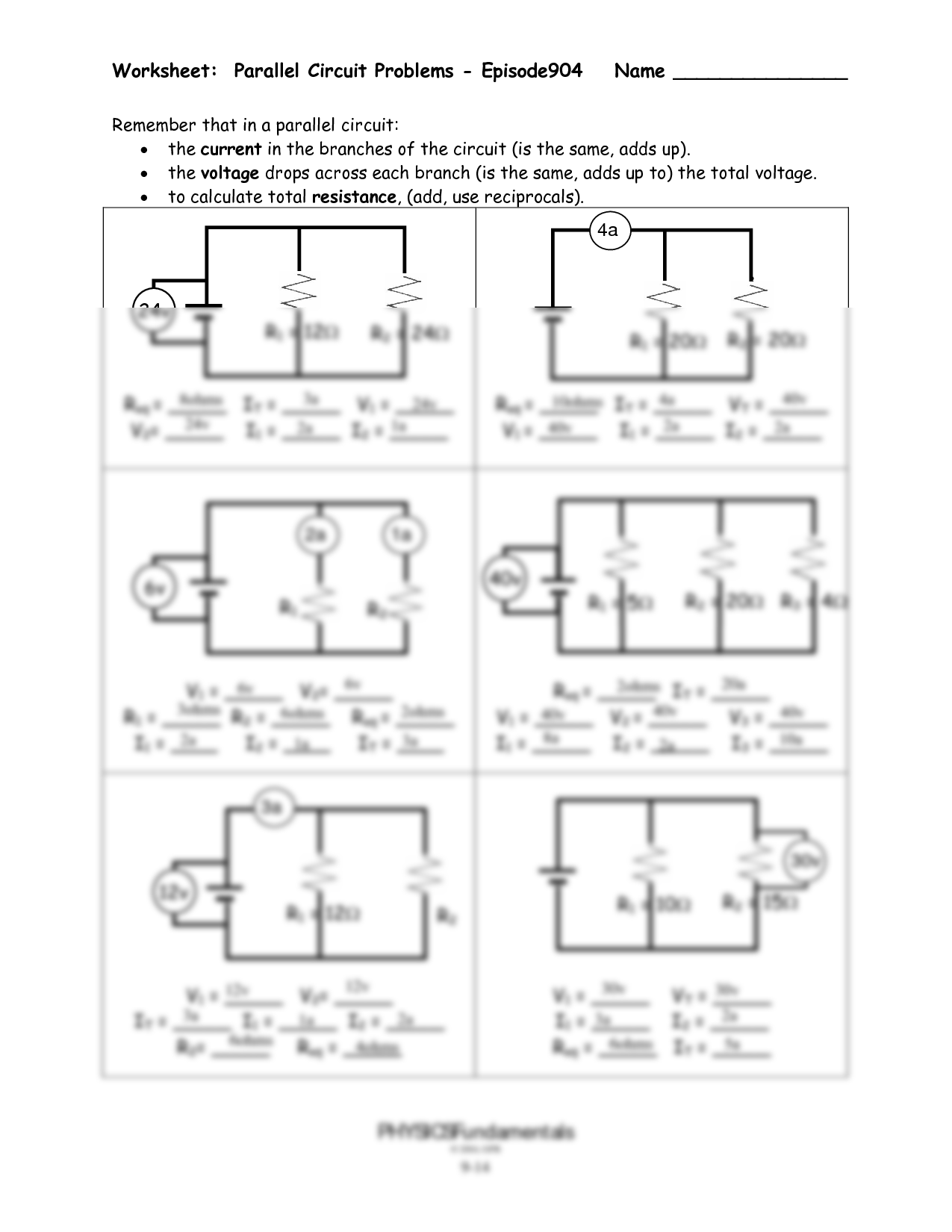
Mastering Parallel Circuits: Problem Solving Worksheet
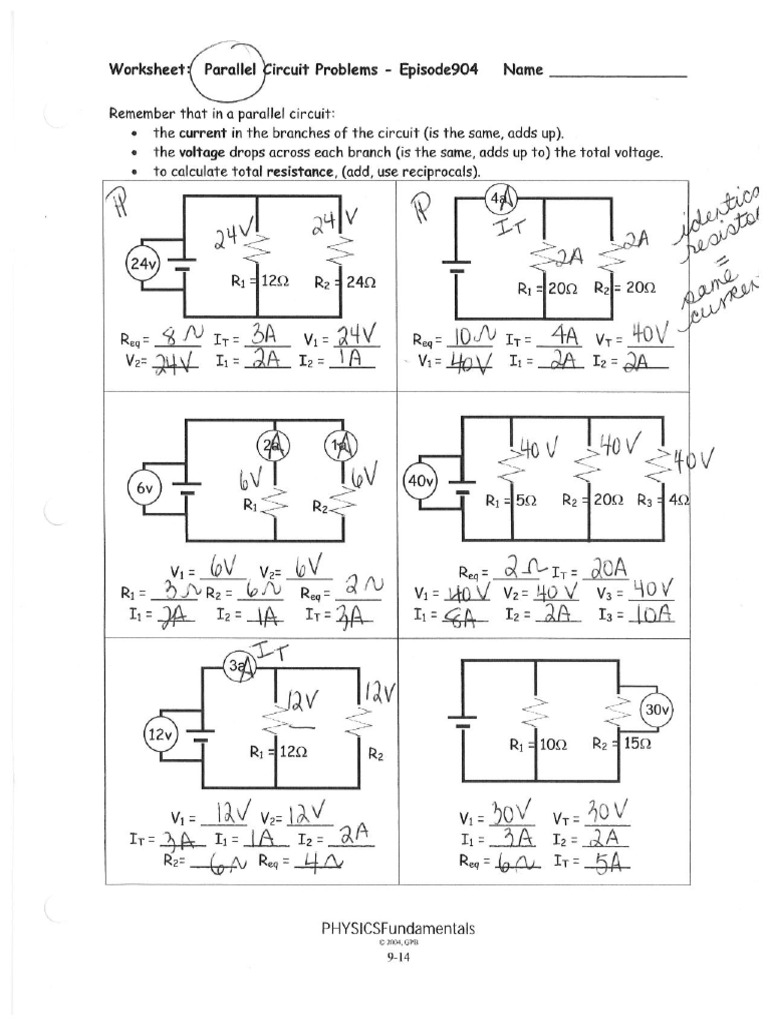
Parallel circuits are a fundamental part of electrical engineering and physics. Unlike series circuits, parallel circuits provide multiple pathways for current to flow, making them essential in numerous real-world applications from home wiring to electronic devices. In this blog post, we delve deep into the world of parallel circuits, exploring their principles, calculations, and practical problem-solving techniques.
Understanding the Basics of Parallel Circuits

In a parallel circuit, components are connected in such a way that each has its own distinct electrical path. Here are some key features:
- Current Division: The total current from the power source divides among the parallel branches. The current in each branch is proportional to the resistance of that branch.
- Voltage Consistency: All components in parallel experience the same voltage drop as they are directly connected to the voltage source.
- Resistor Combination: The total resistance of parallel circuits decreases as more resistors are added in parallel.
💡 Note: Remember, in parallel circuits, current adds up while voltage remains the same across all branches.
Calculations in Parallel Circuits

Understanding how to calculate current, voltage, and resistance in parallel circuits is crucial for mastering this subject. Here’s how you can approach these calculations:
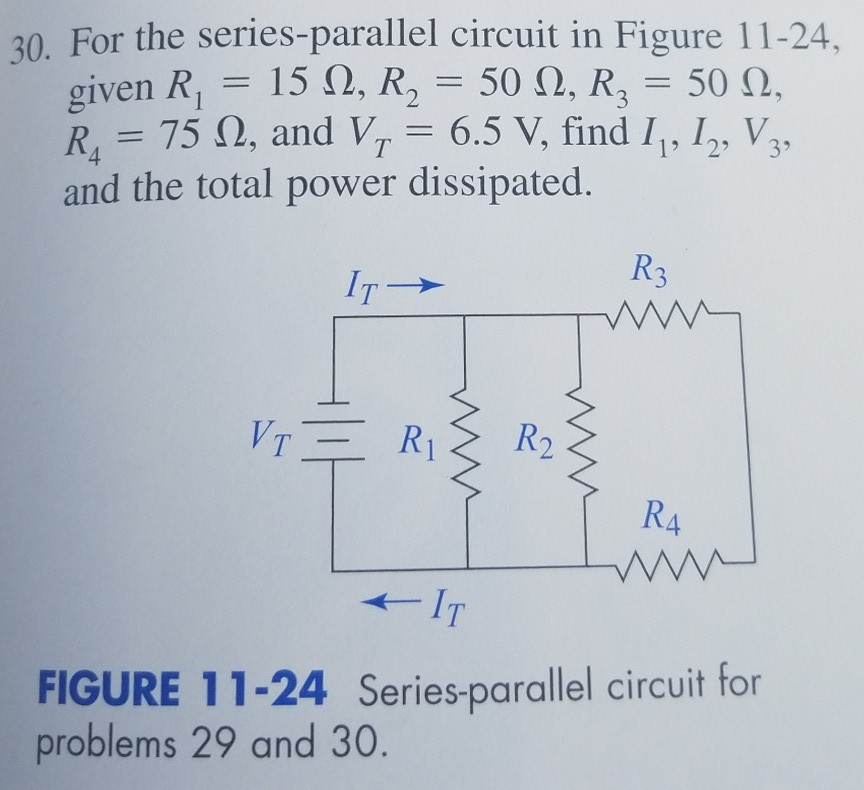
Total Resistance Calculation
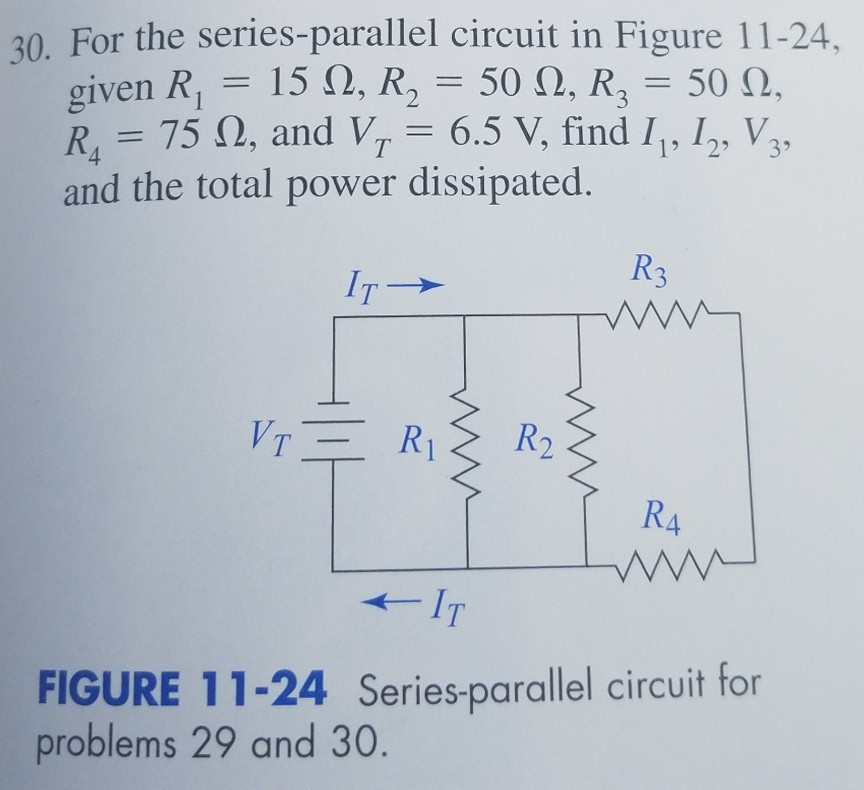
The total resistance (R{total}) in a parallel circuit can be found using the following formula:
[ \frac{1}{R{total}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + … ]📌 Note: When solving for R_{total}, you need to find the reciprocal of the sum of the reciprocals of each resistor's resistance.
Current Division
The current through any branch can be calculated using Ohm’s Law. If (I_{total}) is the total current and (I_n) is the current through a resistor (R_n), then:
[ In = \frac{R{total}}{Rn} \times I{total} ]Voltage
As all resistors share the same voltage source, the voltage across each resistor is:
[ V{R1} = V{R2} = V{R3} = … = V{source} ]Problem Solving Worksheet
Here’s a worksheet that you can use to practice and understand parallel circuits better:
| Problem Number | Problem Description | Given | Solution Steps | Answer |
|---|---|---|---|---|
| 1 | Calculate total resistance | R1 = 2 ohms, R2 = 4 ohms |
|
1.33 ohms |
| 2 | Determine current through each resistor | Total current = 10A, R1 = 3 ohms, R2 = 5 ohms |
|
I1 = 5A, I2 = 5A |
| 3 | Find the voltage across a branch resistor | Source Voltage = 12V, R = 6 ohms |
|
12V |

⚙️ Note: Solving parallel circuit problems involves understanding Ohm's Law, series-parallel resistance calculations, and current division principles.
Real-world Applications

Parallel circuits have numerous applications:
- Home Electrical Wiring: Circuits in homes are often wired in parallel to ensure that if one device fails, others continue to function.
- Electronics: Parallel resistors are used in voltage dividers and current limiting circuits.
- Power Distribution: Large electrical networks use parallel circuits for efficient power distribution.
By understanding parallel circuits, you gain the ability to design and troubleshoot more complex electrical systems. From ensuring safety in home wiring to optimizing electronic devices for better performance, the knowledge of parallel circuits is invaluable.
In recapitulating, parallel circuits are distinguished by their ability to provide multiple paths for current flow, resulting in shared voltage and divided current among branches. Calculating total resistance, understanding current division, and troubleshooting issues within these circuits are key skills for anyone involved in electrical design or electronics. This knowledge allows for the creation of efficient, reliable, and safe electrical systems, which are crucial in our increasingly electronic world.
What is the primary benefit of using parallel circuits?

+
The main benefit is that failure in one branch does not affect others, providing redundancy and safety in electrical systems.
How do you calculate the total resistance in a parallel circuit?

+
You sum the reciprocals of each resistor’s resistance, then take the reciprocal of that sum.
What happens if you add more resistors in parallel to a circuit?

+
The total resistance of the circuit decreases, which can lead to an increase in the overall current if the voltage source remains constant.



