Rational vs. Irrational Numbers: 5 Key Distinctions

Understanding the fundamental nature of numbers is crucial for both academic learning and practical applications in various fields like engineering, finance, and computer science. Numbers are broadly classified into two groups: rational numbers and irrational numbers. These two categories are not only mathematically distinct but also have unique properties and uses. In this comprehensive guide, we'll delve into the five key distinctions between rational and irrational numbers, exploring their characteristics, applications, and the ways they interact within the number system.
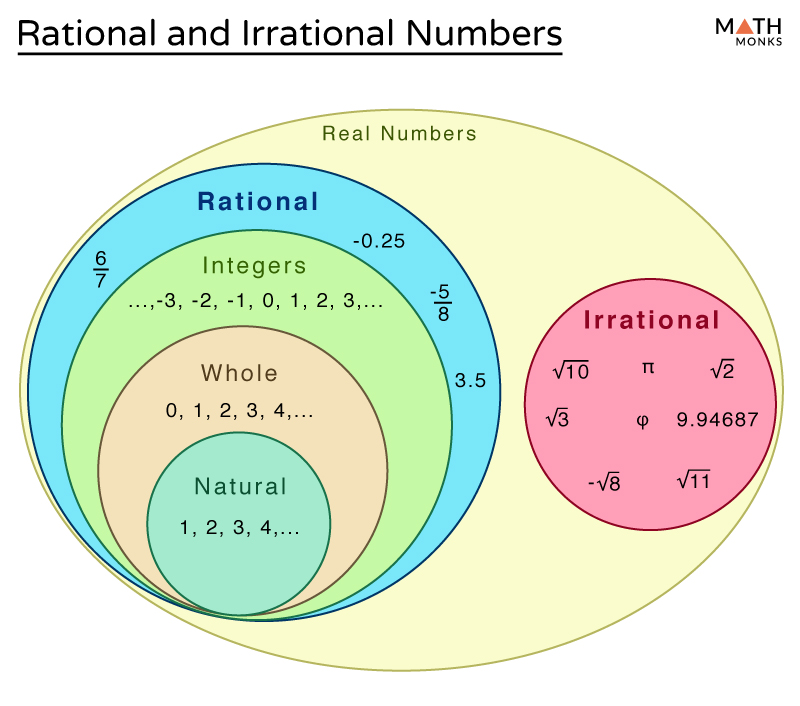
1. Definition and Structure

- Rational Numbers: A rational number can be expressed as the quotient or fraction of two integers, where the denominator is not zero. This includes all integers, fractions, decimals, and repeating decimals. Formally, a rational number p can be written as: [ p = \frac{a}{b}, \text{ where } a, b \in \mathbb{Z} \text{ and } b \neq 0 ] Here, a and b are integers, b is non-zero, and the fraction is in its simplest form.
<li><strong>Irrational Numbers:</strong> An irrational number cannot be expressed as a simple fraction. These numbers have non-repeating, non-terminating decimal representations. Examples include <i>π</i>, <i>√2</i>, <i>e</i>, and <i>√3</i>. Irrational numbers do not fit into any regular arithmetic pattern.</li>
💡 Note: The distinction between rational and irrational numbers becomes clearer when dealing with real-life problems involving measurements, where precise accuracy is necessary.
2. Representation in the Number Line

- Rational Numbers: They are dense on the number line, meaning between any two rational numbers, there exist infinitely many other rational numbers.
- Irrational Numbers: While irrational numbers also fill the number line, they are not discrete; instead, they are dense in the sense that between any two irrational numbers, there are infinite irrational and rational numbers.
This distinction leads to intriguing properties when dealing with limits, calculus, and continuity in real numbers.
3. Behavior in Equations and Operations
- Rational Numbers: Operations like addition, subtraction, multiplication, and division can yield either rational or irrational results, but arithmetic with rational numbers generally remains within the rational domain unless specified otherwise.
- Irrational Numbers: Operations on irrational numbers often result in irrational outcomes. For example, adding √2 and √3 does not simplify to a rational number, highlighting their distinct nature in arithmetic.
| Operation | Rational Result | Irrational Result |
|---|---|---|
| Addition/Subtraction | √2 + √2 = 2√2 (still irrational) | √2 + √3 (irrational) |
| Multiplication | √3 * √3 = 3 (rational) | √2 * √5 (irrational) |
| Division | √3 / √3 = 1 (rational) | √2 / √3 (irrational) |

💡 Note: Operations with irrational numbers can unexpectedly yield rational numbers in some cases, like squaring the square root of a number.
4. Applications in Real World

- Rational Numbers:
- Currency: Prices, payments, and bank interest rates are expressed in rational numbers.
- Measurements: Everyday measurements like length, weight, or volume often use rational numbers for practicality.
- Engineering: Many physical constants and standardized measurements are rational.
<li><strong>Irrational Numbers:</strong>
<ul>
<li>Mathematical Constants: <i>π</i> for circumference calculations, <i>e</i> for exponential growth.</li>
<li>Geometry: Diagonals of squares or any non-right triangle's hypotenuse.</li>
<li>Science: Used in models of physical phenomena like the normal distribution in statistics.</li>
</ul>
</li>
5. Set Membership and Number Theory

- Rational Numbers: They form a subset of the real numbers, and their density on the number line is due to their closure under basic arithmetic operations.
- Irrational Numbers: These numbers are also real numbers but are not countable. Their presence within the real numbers adds infinite density, yet their algebraic properties often resist simplification through traditional arithmetic.
In wrapping up, the distinctions between rational and irrational numbers provide a rich landscape for mathematical exploration and real-world application. Rational numbers, with their clear structure and representation, offer a foundation for computational arithmetic and practical calculations. Conversely, irrational numbers introduce complexity, infinity, and beauty into the mathematical universe, often manifesting in nature's patterns and modern technology. Their interplay within the number system underscores the elegance and intricacy of mathematics, pushing the boundaries of our understanding and application of numbers.
Can the sum of two irrational numbers be rational?

+
Yes, it’s possible. For example, √2 + (-√2) equals zero, which is a rational number.
Why are irrational numbers important in mathematics?

+
Irrational numbers help in understanding concepts like infinity, continuity, and the nature of numbers beyond our usual arithmetic. They are crucial in areas like calculus, where dealing with infinite limits and series is common.
How do irrational numbers affect everyday life?

+
While most everyday calculations use rational numbers, irrational numbers are integral to fields like architecture, engineering, and finance, where precise measurements or complex calculations are necessary. For instance, π is used in designing circular structures, and irrational numbers underpin many financial models.