Master Matrices: Free Practice Worksheet for All Levels

Learning and mastering matrices can open up a world of opportunities in mathematics, engineering, physics, computer science, and data analysis. Whether you're a beginner tackling matrix concepts for the first time or an advanced learner looking to deepen your understanding, matrices are a fundamental tool in algebra and beyond. In this detailed blog post, we'll explore how you can practice and excel in matrices, regardless of your skill level, using a free worksheet designed for self-improvement.
Why Matrices Matter

Matrices are more than just arrays of numbers; they are powerful tools for:
- Linear transformations
- Solving systems of linear equations
- Data organization and analysis
- Graph theory
- Computer graphics
Understanding matrices thoroughly can significantly boost your problem-solving abilities across numerous fields.
The Free Matrices Worksheet

We’ve created a comprehensive worksheet tailored to help you practice matrix operations and deepen your understanding at all levels. Here’s how it’s structured:
Section 1: Basic Concepts

Begin with the basics:
- Matrix Dimensions - Identify the number of rows and columns in matrices.
- Types of Matrices - Learn about square matrices, rectangular matrices, identity, zero, and diagonal matrices.
- Matrix Addition and Subtraction - Practice with simple operations.
📌 Note: Addition and subtraction of matrices require them to have the same dimensions.
Section 2: Intermediate Matrix Operations
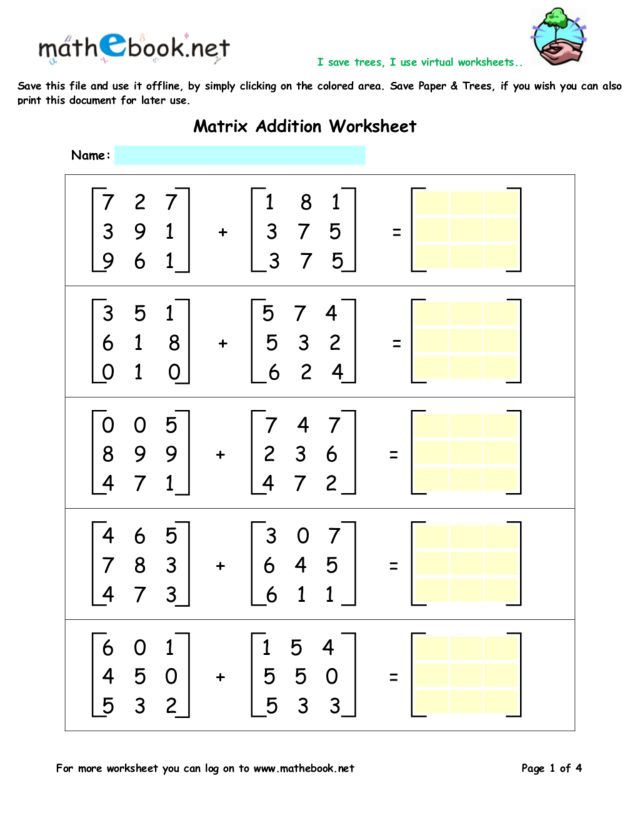
Move to more complex operations:
- Matrix Multiplication - Understand the rules and compute products.
- Transpose - Flip matrices over their diagonals.
- Determinants - Calculate the determinant of 2x2 and 3x3 matrices.
📝 Note: Matrix multiplication is not commutative; the order matters.
Section 3: Advanced Topics
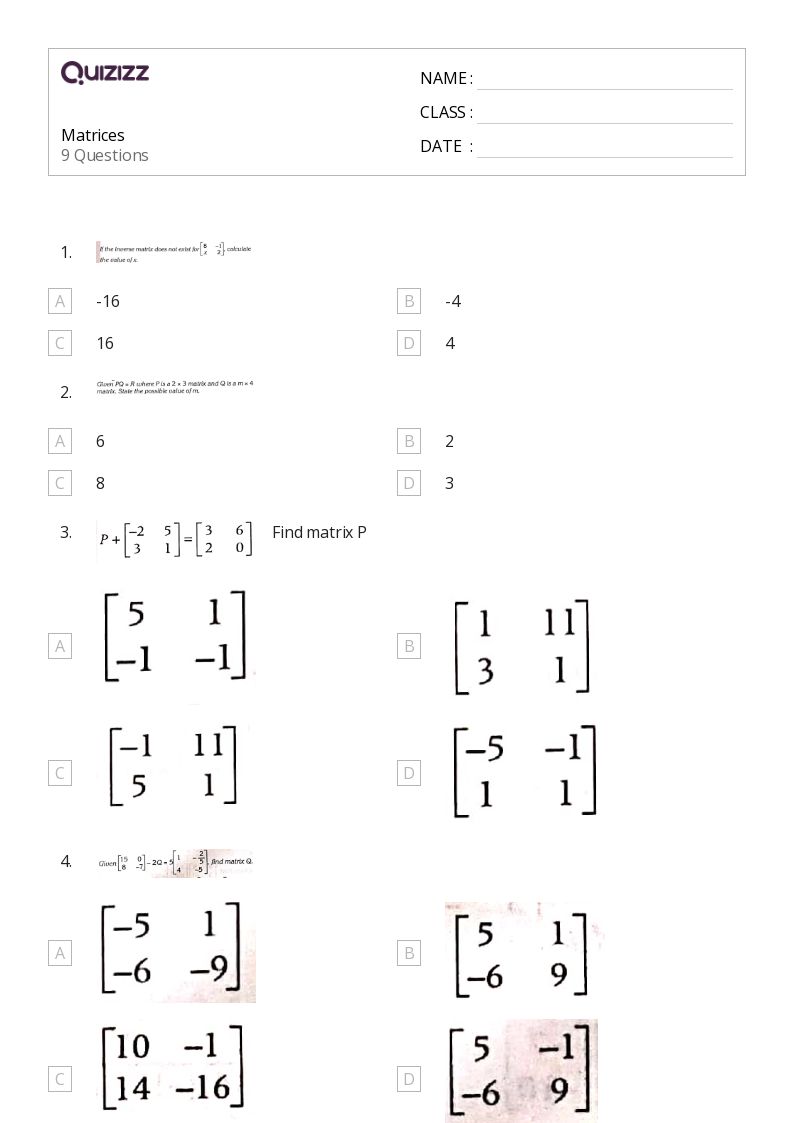
Enhance your skills with:
- Inverse Matrices - Find the inverse of matrices and solve equations using inverses.
- Eigenvalues and Eigenvectors - Compute eigenvalues and find corresponding eigenvectors.
- Orthogonal Matrices - Explore the properties of orthogonal matrices and their applications.
Using the Worksheet

Here’s how you can effectively use the worksheet:
- Start with Theory - Review each concept before diving into the exercises.
- Practice Deliberately - Take your time to understand each problem.
- Check Answers - After completing sections, verify your work against provided solutions.
- Set Goals - Aim to master one section at a time.
| Skill Level | Sections to Focus |
|---|---|
| Beginner | Section 1 |
| Intermediate | Sections 1 and 2 |
| Advanced | Sections 1, 2, and 3 |

To wrap up, mastering matrices is not only about performing calculations but also about understanding how these structures interact with each other and represent linear systems. By engaging with our free worksheet, you'll not only practice but also gain a deeper insight into the mathematical elegance of matrices. This journey through basic to advanced topics will empower you to tackle more complex mathematical problems, enhance your problem-solving skills, and possibly discover new applications for matrices in your field of study or work. Remember, persistence and practice are key to success in any mathematical discipline, and matrices are no exception.
Can matrices be divided?

+
Matrices cannot be divided in the traditional sense. Instead, we find the inverse of a matrix and multiply by it to solve equations.
How do I know if a matrix has an inverse?

+
A matrix has an inverse if its determinant is not zero. For square matrices, this means the matrix is non-singular.
What does an eigenvector represent in the context of matrices?
+
An eigenvector represents a vector that doesn’t change direction when the matrix transformation is applied, only getting scaled by a scalar value known as the eigenvalue.
Are there any real-world applications of matrix inversion?

+
Yes, matrix inversion is used in applications like cryptography, optimization in operations research, solving systems of linear equations in electrical circuits, and more.



