Mastering Independent and Dependent Probabilities: Engaging Worksheet

Understanding the difference between independent and dependent probabilities is crucial in many fields, from gambling to weather forecasting and beyond. Whether you're a student tackling probability and statistics or a professional looking to refine your decision-making skills, diving into the concepts through practical exercises can provide a solid foundation. This post will guide you through crafting an engaging worksheet focused on mastering these concepts.
Theoretical Foundation

Before we dive into worksheet creation, it’s essential to understand the basics:
- Independent Events: The occurrence of one event does not affect the probability of another. For example, flipping a coin twice; the outcome of the first flip doesn’t influence the second.
- Dependent Events: The occurrence of one event does indeed influence the probability of another event. For example, drawing a card from a deck and then drawing another without replacing the first card.
Designing Your Worksheet

To make your worksheet engaging and educational, consider the following structure:
Section 1: Introduction to Probability

Start with definitions and examples to set the stage:
- Define independent and dependent probabilities with everyday examples.
- Include a simple formula for calculating probability, like P(A and B) = P(A) * P(B) for independent events.
Section 2: Interactive Problems

This section should challenge students to apply the concepts:
- Problem Set 1: Independent Events
- Calculate the probability of flipping two coins and both landing heads.
- Determine the likelihood of drawing a red card followed by another red card with replacement.
🎲 Note: Remember to remind students to consider the independence of events when solving these problems.
<li><strong>Problem Set 2: Dependent Events</strong>
<ol>
<li>Find the probability of drawing a king from a standard deck and then another king without replacement.</li>
<li>Work out the chances of choosing two marbles from a bag of 10 (4 red, 6 blue) without replacement.</li>
</ol>
</li>
| Event | Independent or Dependent | Outcome A | Outcome B | P(A and B) |
|---|---|---|---|---|
| Flipping coins | Independent | Heads | Heads | 1/4 or 25% |
| Drawing cards | Dependent | King | King | 1/169 or 0.59% |

Section 3: Real-World Applications

To make the concepts relatable, include problems based on real-life scenarios:
- Traffic light sequences
- Weather forecasts (rain today, rain tomorrow)
- Insurance assessments for consecutive years
Section 4: Advanced Challenges
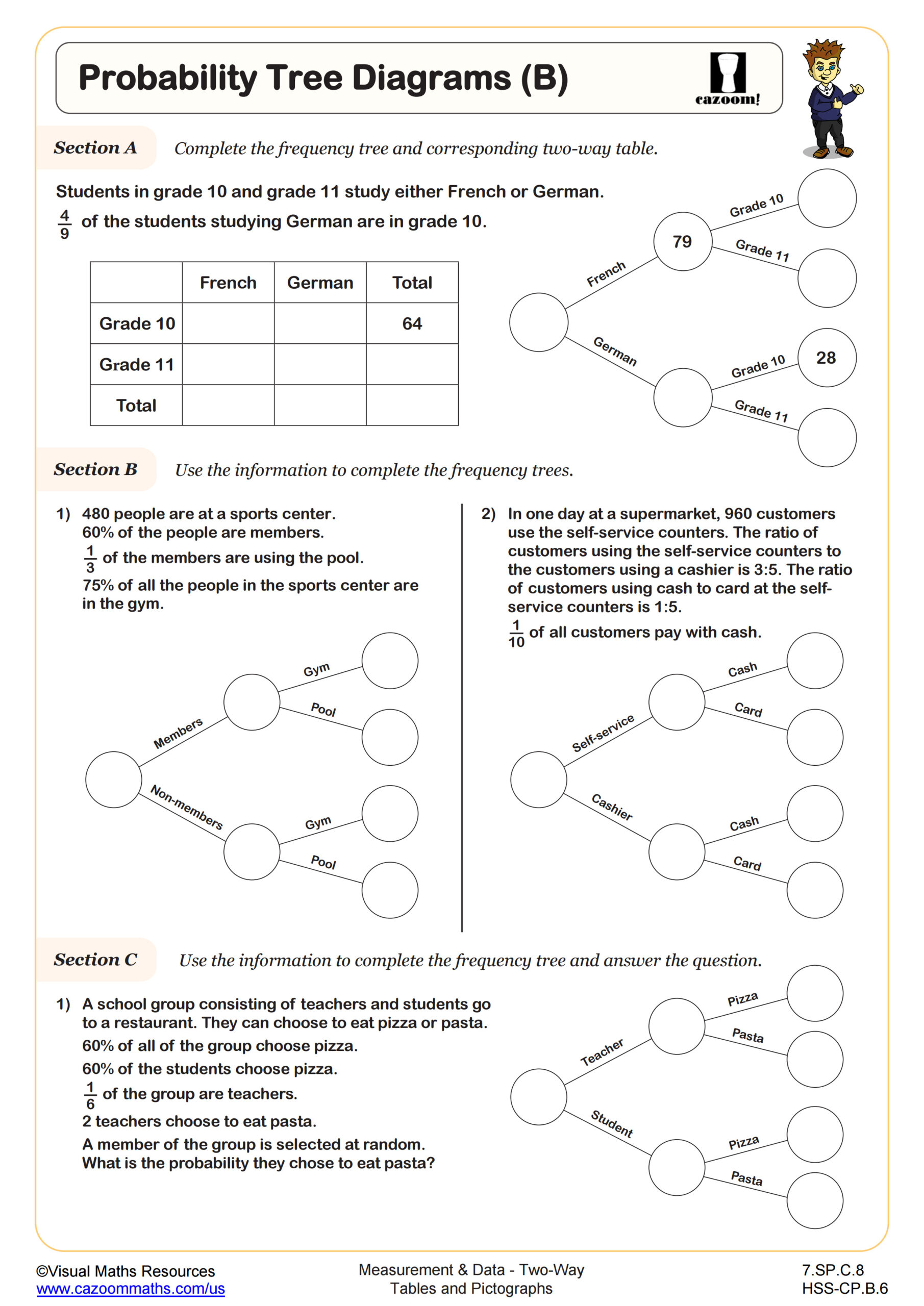
This section can push the boundaries of what students have learned:
- Create a tree diagram to visualize compound events.
- Analyze games of chance like roulette or lotteries.
Final Recap

Summarize the key points covered in the worksheet, reinforcing:
- The distinction between independent and dependent events.
- Formulas used for probability calculations.
- Real-world applications to make the concept tangible.
As you work through this worksheet, the differentiation between independent and dependent probabilities should become clearer. Each problem set is designed not just to test understanding but also to build intuition about how events can interact or stand alone. By engaging with these exercises, learners will gain a deeper appreciation for the nuances of probability, which will aid them in both theoretical and practical problem-solving scenarios.
What makes an event independent?

+
An event is independent when the occurrence of one event does not influence the probability of the other event occurring.
How do you calculate the probability of dependent events?

+
To calculate the probability of dependent events, you use conditional probability. The formula is P(A and B) = P(A) * P(B|A), where P(B|A) is the probability of event B given that event A has occurred.
Can you give an example of a real-life dependent probability scenario?

+
Yes, consider the probability of drawing two aces from a deck of cards without replacement. After drawing the first ace, the deck has fewer cards, thus changing the probability for the second draw.



