5 Answers for the Distance Formula Worksheet

Understanding distance calculation is a key part of geometry and algebra, specifically when dealing with the coordinate plane. Whether you're plotting points, calculating the distance between cities on a map, or solving a physics problem, the distance formula is an essential tool in your mathematical toolkit. Here, we'll walk through 5 Answers for the Distance Formula Worksheet, providing detailed explanations to help you grasp the concept thoroughly.
The Distance Formula Basics
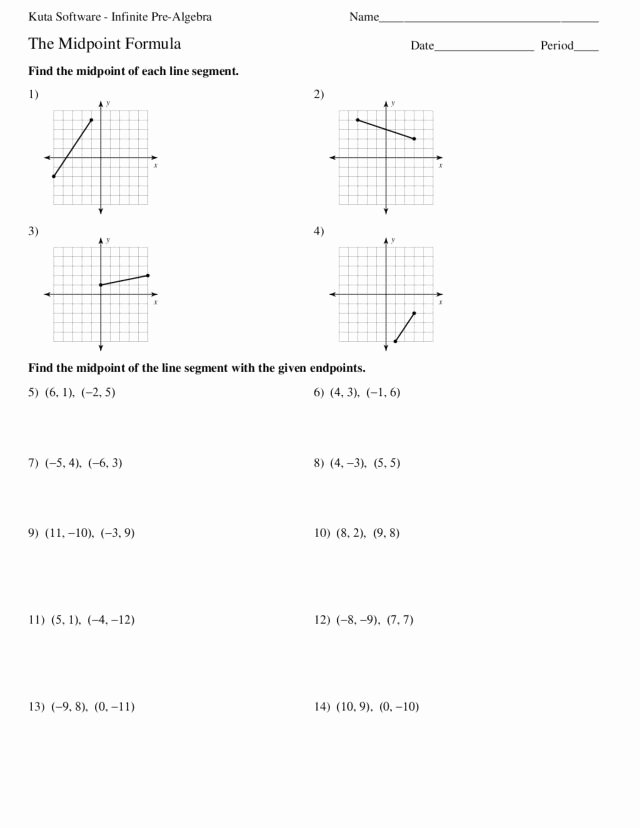
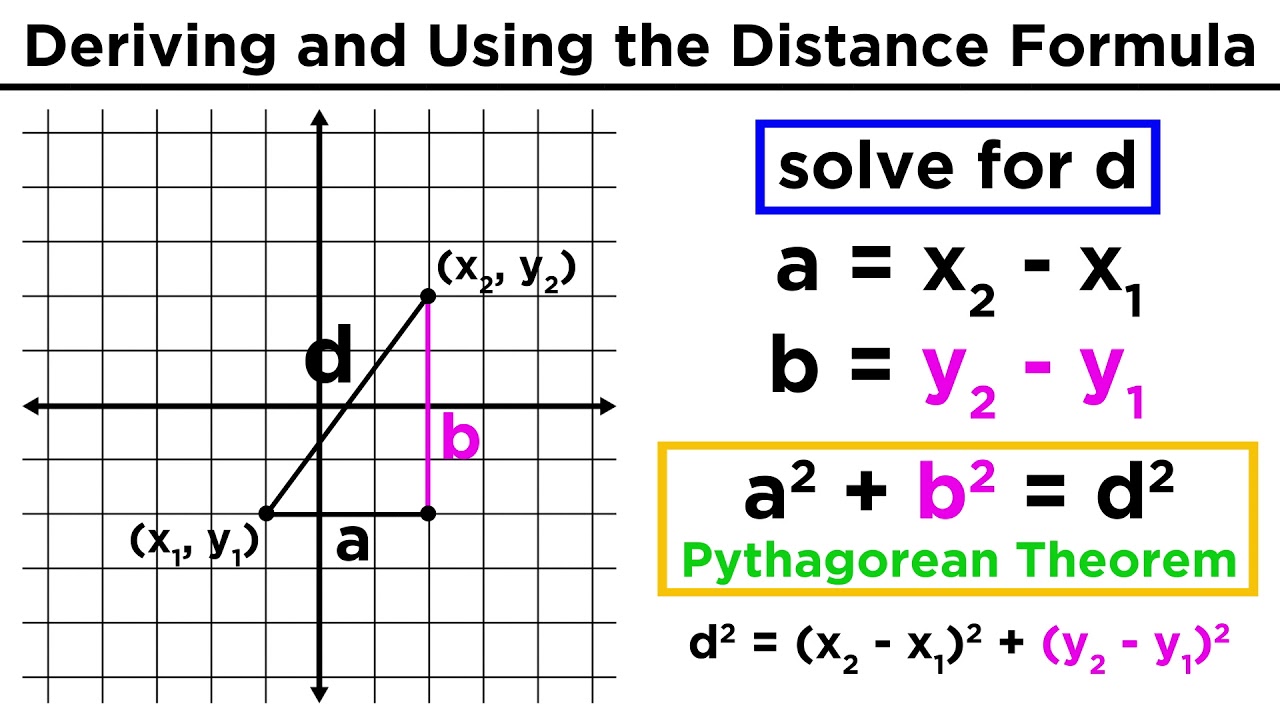
Before we delve into specific answers, let’s review the distance formula:
The distance between two points ((x_1, y_1)) and ((x_2, y_2)) on the Cartesian coordinate plane is given by:
[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} ]Answer 1: Calculating the Distance Between Points

Problem: Find the distance between points ((3, 4)) and ((8, 15)).

- Identify the points: ((x_1, y_1) = (3, 4)) and ((x_2, y_2) = (8, 15)).
- Plug the values into the distance formula: [ d = \sqrt{(8 - 3)^2 + (15 - 4)^2} ] [ d = \sqrt{5^2 + 11^2} ] [ d = \sqrt{25 + 121} ] [ d = \sqrt{146} ] [ d \approx 12.08 ]
💡 Note: When calculating, make sure to double-check the arithmetic, especially when squaring and adding numbers.
Answer 2: Simplifying the Distance Calculation

Problem: Calculate the distance between ((-5, 3)) and ((7, -7)).
- Here are the coordinates: ((x_1, y_1) = (-5, 3)) and ((x_2, y_2) = (7, -7)).
- Apply the formula: [ d = \sqrt{(7 - (-5))^2 + (-7 - 3)^2} ] [ d = \sqrt{12^2 + (-10)^2} ] [ d = \sqrt{144 + 100} ] [ d = \sqrt{244} ] [ d \approx 15.62 ]
Answer 3: Using Distance in Real-World Scenarios

Problem: An airplane is at an altitude of 10,000 meters directly above point ((150, 200)), and a ground station is at ((0, 0)). How far is the plane from the ground station?
| Point | X Coordinate | Y Coordinate | Z Coordinate (Altitude) |
|---|---|---|---|
| Ground Station | 0 | 0 | 0 |
| Airplane | 150 | 200 | 10,000 |

Using a 3D version of the distance formula: [ d = \sqrt{(150 - 0)^2 + (200 - 0)^2 + (10,000 - 0)^2} ] [ d = \sqrt{150^2 + 200^2 + 10,000^2} ] [ d \approx 10,022.5 \text{ meters} ]
Answer 4: The Pythagorean Theorem Relationship

Problem: Find the distance from the origin ((0, 0)) to the point ((6, 8)).
- Directly apply the distance formula: [ d = \sqrt{(6 - 0)^2 + (8 - 0)^2} ] [ d = \sqrt{36 + 64} ] [ d = \sqrt{100} ] [ d = 10 ]
This problem demonstrates how the distance formula is essentially the Pythagorean theorem applied in a coordinate system.
Answer 5: Distance Between a Series of Points
Problem: Calculate the total distance if you travel from ((1, 2)) to ((4, 6)) then to ((7, 3)) in a straight line.
- First, calculate the distance from ((1, 2)) to ((4, 6)): [ d1 = \sqrt{(4 - 1)^2 + (6 - 2)^2} ] [ d1 = \sqrt{3^2 + 4^2} ] [ d1 = \sqrt{9 + 16} ] [ d1 = \sqrt{25} ] [ d1 = 5 ]
- Next, calculate the distance from ((4, 6)) to ((7, 3)): [ d2 = \sqrt{(7 - 4)^2 + (3 - 6)^2} ] [ d2 = \sqrt{3^2 + (-3)^2} ] [ d2 = \sqrt{9 + 9} ] [ d2 = \sqrt{18} ] [ d2 \approx 4.24 ]
- Add the distances: [ \text{Total Distance} \approx 5 + 4.24 \approx 9.24 ]
In wrapping up these examples, we’ve seen how the distance formula can be applied in various contexts, from simple coordinate calculations to real-world scenarios. Understanding this formula and practicing with these types of problems will enhance your ability to work with spatial relationships and geometric calculations effectively.
What are the practical applications of the distance formula?

+
The distance formula is used in navigation systems, geographical mapping, physics for calculating distances in 3D space, computer graphics for rendering distances, and in engineering for spatial calculations.
How does the distance formula relate to the Pythagorean theorem?

+
The distance formula is a direct application of the Pythagorean theorem. If you have a right triangle with the legs corresponding to the differences in x and y coordinates, the distance between the two points forms the hypotenuse.
Can the distance formula be used in higher dimensions?

+
Yes, the formula can be extended to any number of dimensions. For n-dimensional space, you sum the squares of the differences in coordinates for each dimension, then take the square root.
Is there a quicker way to calculate distances if one point is the origin?

+
If one point is the origin ((0, 0)), you only need to find the square root of the sum of the squares of the other point’s coordinates. For ((x, y)), the distance is (\sqrt{x^2 + y^2}).
What are common mistakes when using the distance formula?

+
Common errors include forgetting to square the differences, not adding the correct number of dimensions, or miscalculating the square root. Also, not taking the absolute value of the differences can lead to mistakes in subtraction.