Fractions to Decimals to Percents: Free Worksheet Inside

When you're exploring the world of mathematics, understanding the relationships between fractions, decimals, and percents is crucial. These fundamental concepts not only form the bedrock of arithmetic but also enhance your ability to solve everyday problems, from financial calculations to cooking. This blog post will delve into these relationships, guide you through converting between them, and provide practical examples, culminating in a free worksheet to reinforce your skills.
Understanding Fractions

A fraction represents a part of a whole. The number on the top (numerator) tells us how many equal parts we have, and the number on the bottom (denominator) indicates how many equal parts the whole is divided into. Here’s how you can grasp this concept:
- Simplification: Reducing a fraction to its simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD).
- Proper and Improper Fractions: Proper fractions have a numerator smaller than the denominator (e.g., 1/2), while improper fractions have the numerator greater than or equal to the denominator (e.g., 3/2).
Converting Fractions to Decimals

To convert a fraction to a decimal, you divide the numerator by the denominator:
- Long Division: Use long division to find the decimal equivalent. For example, 3/4 becomes 3 ÷ 4, which equals 0.75.
- Terminating vs. Non-Terminating: Some fractions will convert to a terminating decimal (e.g., 1/2 = 0.5), while others will be non-terminating (e.g., 1/3 ≈ 0.3333…).
Converting Fractions to Percents

A percent means per hundred, so to convert a fraction to a percent, follow these steps:
- Multiply by 100: Convert the fraction to a decimal first, then multiply by 100 to get the percentage. For 1/4, you would multiply 0.25 by 100, resulting in 25%.
- Alternative Method: You can also divide the numerator by the denominator, then multiply the result by 100 directly. For example, 1/4 × 100 = 25.
Converting Decimals to Fractions
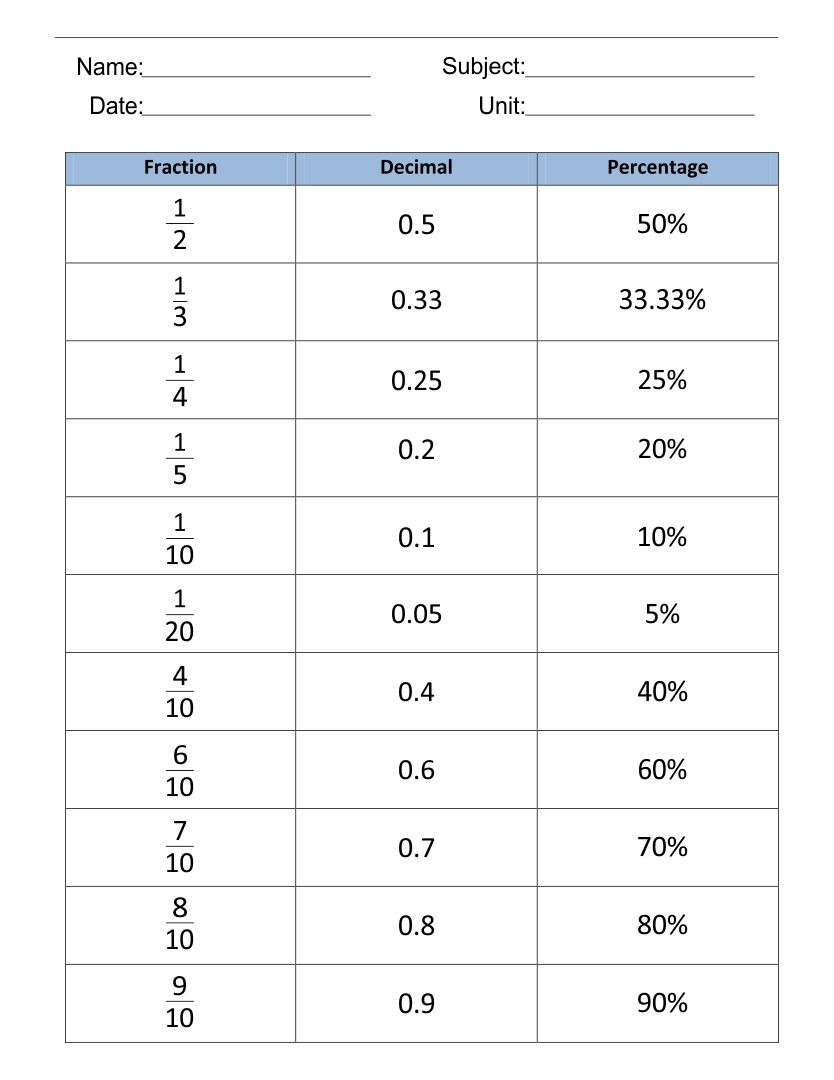
To change a decimal into a fraction, follow these steps:
- Identify Place Value: Determine the place value of the last digit in the decimal. For example, in 0.75, the place value is hundredths.
- Convert to Fraction: Use the decimal’s place value as the denominator (e.g., for 0.75, 100) and the decimal as the numerator, then simplify if possible. Here, 75/100 simplifies to 3/4.
🗣️ Note: For repeating decimals, you'll need to use algebraic methods to convert them to fractions, but this is beyond our scope here.
Decimals to Percents

Converting decimals to percents is straightforward:
- Multiply by 100: Simply multiply the decimal by 100 and add a percentage sign. For instance, 0.45 becomes 45%.
Percents to Fractions

To convert a percent to a fraction:
- Divide by 100: Replace the percent sign with ‘per 100’ and then simplify the fraction. For 60%, you would write it as 60/100, which simplifies to 3/5.
Practical Applications

Let’s explore how these conversions are applied in real-life scenarios:
- Cooking: Adjusting recipes based on the number of servings requires converting between fractions and decimals (e.g., converting 3/4 cup to 0.75 cup).
- Discounts and Sales: Understanding that a 20% discount means you pay 80% of the original price involves converting the percent to a fraction or decimal.
- Financial Calculations: Interest rates, taxes, and inflation rates are commonly expressed in percentages, requiring conversions to understand and compute effectively.
Free Worksheet

Here is a table where you can practice your conversions:
| Fraction | Decimal | Percent |
|---|---|---|
| 1/2 | ||
| 0.375 | ||
| 75% | ||
| 3/8 | ||
| 0.125 |

Complete the worksheet above to reinforce your understanding of converting between fractions, decimals, and percentages.
By now, you should have a clearer picture of how to convert between fractions, decimals, and percents. These concepts not only improve your mathematical skills but also enhance your everyday problem-solving abilities. Use the provided worksheet to practice these conversions, ensuring your comfort with these vital mathematical relationships. Whether you're calculating discounts or resizing recipes, the ability to fluidly navigate between these numerical forms will prove invaluable.
Why is it important to know how to convert between fractions, decimals, and percents?

+
Understanding these conversions is crucial for various everyday calculations, from adjusting recipes to understanding discounts and interest rates in financial transactions. They also underpin many mathematical operations and are fundamental in higher-level mathematics and sciences.
How can I tell if a fraction will convert to a terminating or non-terminating decimal?

+
A fraction will convert to a terminating decimal if the denominator, when reduced to its lowest terms, only has factors of 2 and/or 5. If there are other prime factors, it will result in a repeating decimal.
Can I always simplify a fraction by dividing the numerator and denominator by the same number?

+
Yes, you can always simplify a fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), but not all fractions will simplify to a smaller form if there is no common divisor greater than 1.
Is there a shortcut for converting common fractions to decimals?

+
For common fractions like 1/4 = 0.25, 1/2 = 0.5, or 3/4 = 0.75, it’s useful to memorize these or recognize the pattern in their decimal equivalents.



