5 Coulomb's Law Calculations You Can Easily Master

Electricity and magnetism form the backbone of numerous technological advancements, ranging from simple circuits to complex electromagnetic devices. At the heart of these phenomena lies Coulomb's Law, which dictates the force between two charged particles. For students and hobbyists keen on mastering electrical concepts, understanding and calculating with Coulomb's Law is essential. Here are five straightforward examples to demystify Coulomb's Law:
The Basics of Coulomb’s Law
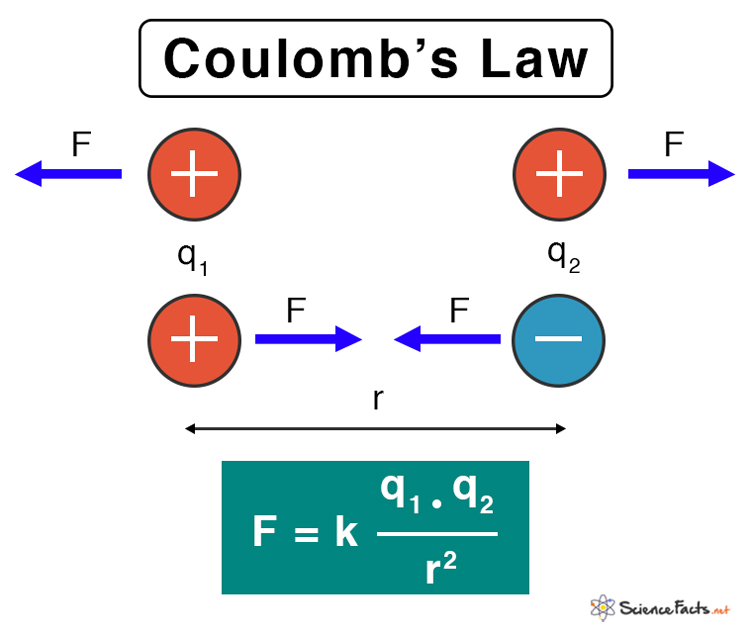
Before diving into specific calculations, let’s review the fundamental equation:
Coulomb’s Law: ( F = k_e \frac{q_1 q_2}{r^2} )
- F - Force between the charges (in Newtons, N)
- ke - Coulomb’s constant ( (8.988 \times 10^9 \, \text{Nm}^2/\text{C}^2))
- q1 and q2 - Magnitude of charges (in Coulombs, C)
- r - Distance between the centers of the charges (in meters, m)
💡 Note: To simplify calculations, often scientific notation is used for numbers like (k_e).
Example 1: Calculating the Force Between Two Point Charges

Consider two point charges with charges ( q_1 = +3 \times 10^{-6} \, \text{C} ) and ( q_2 = -2 \times 10^{-6} \, \text{C} ), placed 1 meter apart:
F = k_e * (q_1 * q_2) / r^2 F = (8.988 × 10^9) * (3 × 10^−6) * (-2 × 10^−6) / 1^2 F = -53.93 × 10^−3 N
The negative sign indicates that the force is attractive.
Example 2: Force on Three Charges in a Line

Imagine three charges arranged in a line: ( q_1 = +3 \, \text{nC} ), ( q_2 = -2 \, \text{nC} ), and ( q_3 = +1 \, \text{nC} ), spaced at 5 cm intervals. Calculate the net force on ( q_2 ):
The force between ( q_1 ) and ( q2 ) is:
F{12} = k_e * (q_1 * q2) / (0.05)^2
F{12} = 215.71 × 10^-6 N
The force between ( q_2 ) and ( q3 ) is:
F{23} = k_e * (q_2 * q3) / (0.05)^2
F{23} = -107.85 × 10^-6 N
Summing these forces:
F{net} = F{12} + F_{23} = 215.71 × 10^-6 N - 107.85 × 10^-6 N = 107.86 × 10^-6 N
💡 Note: The forces are vector quantities, so directions must be considered.
Example 3: Force on a Charge in an Electric Field

Suppose a charge ( q = +5 \, \text{nC} ) is placed in an electric field with strength ( E = 2 \times 10^5 \, \text{N/C} ):
The force experienced by the charge is:
F = q * E F = 5 × 10^-9 * 2 × 10^5 F = 10^-3 N
Example 4: Relationship Between Electric Field and Charge
An electric field arises due to the presence of charges. Using Coulomb’s Law, let’s find the electric field produced by a charge ( q = +2 \times 10^{-6} \, \text{C} ) at a distance of 2 meters:
E = k_e * q / r^2 E = (8.988 × 10^9) * (2 × 10^-6) / 2^2 E = 4.494 × 10^3 \, N/C
Example 5: Equilibrium of Charges

Three charges, ( q_1 = +2 \, \text{nC} ), ( q_2 = -3 \, \text{nC} ), and ( q_3 = -1 \, \text{nC} ), are at equilibrium. Suppose ( q_1 ) is fixed, and ( q_2 ) and ( q_3 ) are free to move. For equilibrium, the net force on ( q_2 ) must be zero:
| Charge | Distance from q1 (m) | Force (N) |
|---|---|---|
| q1 | 0 | N/A |
| q2 | x (let’s call it r1) | k_e * (2 × 10^-9) * (-3 × 10^-9) / r1^2 |
| q3 | 2r1 | k_e * (2 × 10^-9) * (-1 × 10^-9) / (2r1)^2 |
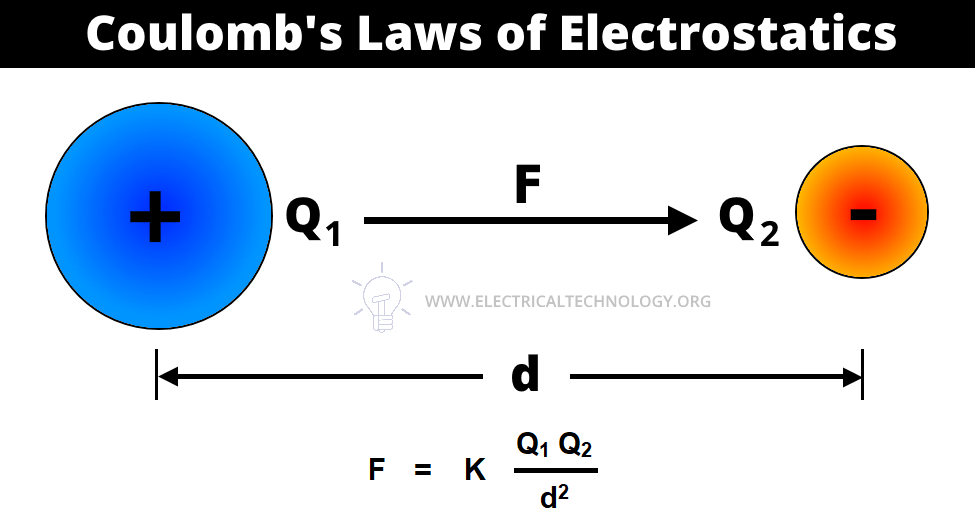
The forces must cancel out:
k_e * (2 × 10^-9) * (-3 × 10^-9) / r1^2 + k_e * (2 × 10^-9) * (-1 × 10^-9) / (2r1)^2 = 0
Solving for ( r1 ) involves recognizing that ( q_2 ) and ( q_3 ) must be on opposite sides of ( q_1 ) for equilibrium.
💡 Note: While solving equilibrium problems, always ensure the directions of forces are correctly accounted for.
In exploring these calculations, you've gained an understanding of how to apply Coulomb's Law in different scenarios, from simple point charges to complex systems in equilibrium. This knowledge not only helps in mastering electrical concepts but also provides a solid foundation for understanding related principles like electric fields and potential. As you continue to study electricity and magnetism, remember that practice, patience, and precision are key to mastering these laws.
What is the importance of the sign in the force calculated from Coulomb’s Law?

+
The sign indicates the direction of the force. A positive sign means the force is repulsive, while a negative sign means it’s attractive. This distinction is crucial for determining whether charges will push apart or come together.
How can we simplify calculations when dealing with Coulomb’s Law?

+
Utilize scientific notation for large or small numbers and ensure accurate units are used. Often, simplifying problems by using symmetry or assuming an equilibrium can reduce the complexity of calculations.
Does Coulomb’s Law work for any type of charge?

+
Yes, Coulomb’s Law applies to both point charges and extended charge distributions. For complex objects, one can approximate charges as point charges or use integration techniques for precise calculations.
How does the distance between charges affect the force?

+
The force decreases inversely with the square of the distance between the charges. Doubling the distance reduces the force to a quarter of its original magnitude, highlighting the inverse square law’s impact.
Can Coulomb’s Law be used to describe magnetic forces?

+
No, Coulomb’s Law describes the interaction between electric charges, whereas magnetic forces are described by Ampere’s Law and the Biot-Savart Law, focusing on current and magnetic fields.