5 Easy Steps to Solve Inequalities Worksheets
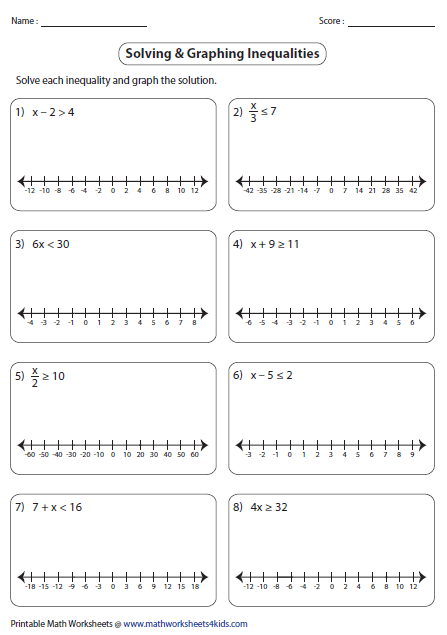
Are you a student grappling with the complexities of mathematics, particularly with solving inequalities? Or perhaps you are an educator looking to make these lessons engaging and understandable? Either way, this comprehensive guide is crafted to simplify the process of tackling inequalities, ensuring you have the tools necessary to excel or teach with confidence.
Understanding Inequalities

Before we delve into practical steps, it’s crucial to understand what inequalities are. An inequality compares two values or expressions, stating that one is not equal to the other. Common types include less than (<), less than or equal to (≤), greater than (>), and greater than or equal to (≥). Let’s break this down further:
- Linear Inequality: Such as 2x + 3 > 5, where x represents a variable, and the goal is to find the values of x that make the statement true.
- Quadratic Inequality: Involving polynomials of degree two or higher, like x2 + 2x - 3 > 0.
- Systems of Inequalities: When there’s more than one inequality to solve simultaneously.
📝 Note: Remember that inequalities often have an infinite number of solutions, unlike equations which typically have a specific solution.
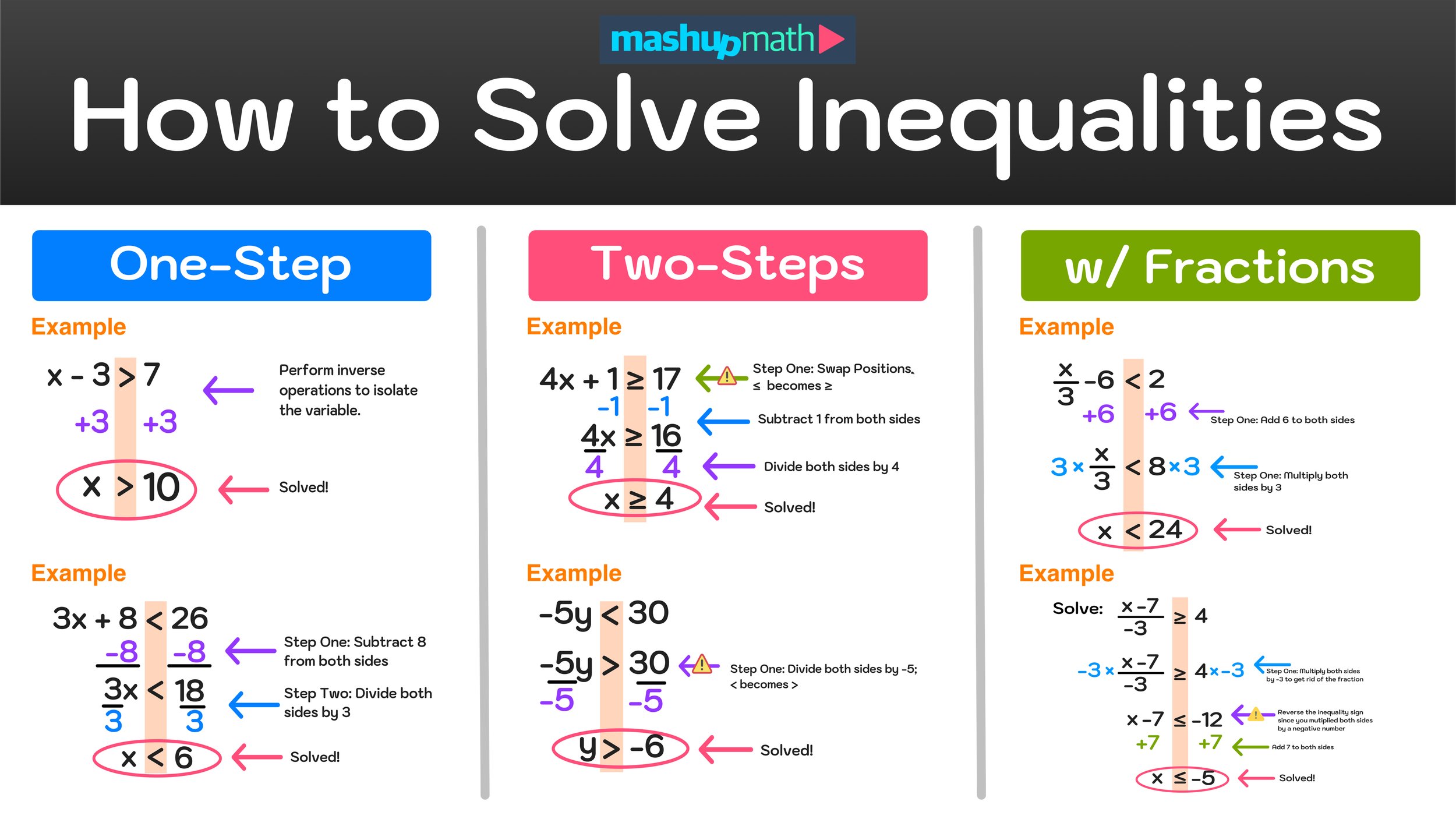
Step 1: Identify the Variables and Constants

When you begin with an inequality, the first step is to distinguish between the variables you’re solving for and the constants. For instance, in the inequality 3x + 4 ≥ 10, x is the variable, while 3, 4, and 10 are constants.
- Identify the variable: Here, it’s x.
- Identify the constants: 3, 4, and 10.
- Note the direction of the inequality sign.
Step 2: Simplify Both Sides

The next step is to simplify the expressions on both sides of the inequality. Here’s how:
- Combine like terms if there are any.
- Subtract or add constants to both sides to isolate the term with the variable.
Example: 3x + 4 ≥ 10
- Subtract 4 from both sides:
3x ≥ 10 - 4
3x ≥ 6
Step 3: Multiply or Divide Both Sides by the Same Number

To isolate the variable, you'll need to perform the same operation on both sides of the inequality. Remember:
- If you multiply or divide both sides by a positive number, the inequality sign remains unchanged.
- If you multiply or divide by a negative number, you must reverse the inequality sign.
Example:
- From step 2: 3x ≥ 6
- Divide both sides by 3:
x ≥ 6 ÷ 3
x ≥ 2
🔄 Note: Always check your solution by substituting back into the original inequality to ensure all steps have been performed correctly.
Step 4: Solve for Systems of Inequalities

When dealing with systems of inequalities, each inequality must be solved independently, then combined. Here’s a structured approach:
- Solve each inequality separately using the above steps.
- Graph each inequality on the coordinate plane if you’re dealing with 2D inequalities.
- Identify the overlapping region as the solution set.
| Example Inequality | Solution Set |
|---|---|
| x + y > 3 | Region above the line x + y = 3 |
| y < 2x - 1 | Region below the line y = 2x - 1 |
| The solution set is where these regions overlap. | |

Step 5: Interpret and Communicate the Solutions

After solving, you need to interpret your results and communicate them effectively, particularly if teaching or explaining:
- Explain that the solution to a single linear inequality can be expressed as an interval or described in words.
- Use visual aids like number lines to depict solutions for 1D inequalities.
- For 2D inequalities or systems, a graphical representation on a coordinate plane is often beneficial.
📚 Note: When presenting solutions, consider the context in which the inequality applies. Real-world problems often require you to discuss the feasibility and implications of the solutions.
In summary, solving inequalities might initially appear daunting due to their abstract nature, but by following these structured steps, you can confidently tackle any inequalities you encounter. From identifying variables and constants to interpreting the results, each step is designed to build your confidence in solving these mathematical puzzles. Whether you're a student or an educator, the ability to navigate inequalities is fundamental in mathematics, opening doors to advanced topics like optimization and real-world problem solving.
What is the main difference between an inequality and an equation?

+
The primary difference is that inequalities compare two expressions indicating their relative size or position, while equations state that two expressions are equal. Inequalities can have multiple solutions or no solution at all, whereas equations typically have a unique solution or set of solutions.
Why do we need to reverse the inequality sign when multiplying or dividing by a negative number?

+
This rule preserves the inequality relationship. Multiplying or dividing by a negative number swaps the relative order of numbers on the number line, thus requiring the sign to be reversed to maintain the correct relationship between the expressions.
Can inequalities have no solutions?
+
Yes, if the conditions set by the inequality are contradictory or impossible to meet, like 5x > 5x + 1, there are no real solutions because no matter what value x takes, the inequality won’t hold true.
How do I teach inequalities to students who are struggling?

+
Start with real-life examples to illustrate the concept. Use visual aids like number lines or coordinate planes to make abstract concepts tangible. Break down each step in the solving process, emphasize why the inequality sign changes with negative multipliers, and provide ample practice with varied problems to build understanding and confidence.