Coordinate Plane Graphing Made Easy: Printable Worksheet

The coordinate plane is an essential tool in mathematics, offering a visual representation of numbers and their relationships. Whether you're a student grappling with geometry or algebra, a teacher looking to provide engaging activities, or a parent assisting with homework, understanding how to graph points on a coordinate plane is crucial. This post will guide you through the basics of coordinate plane graphing, provide practical tips for mastering it, and introduce a printable worksheet to practice this skill.
Understanding the Coordinate Plane
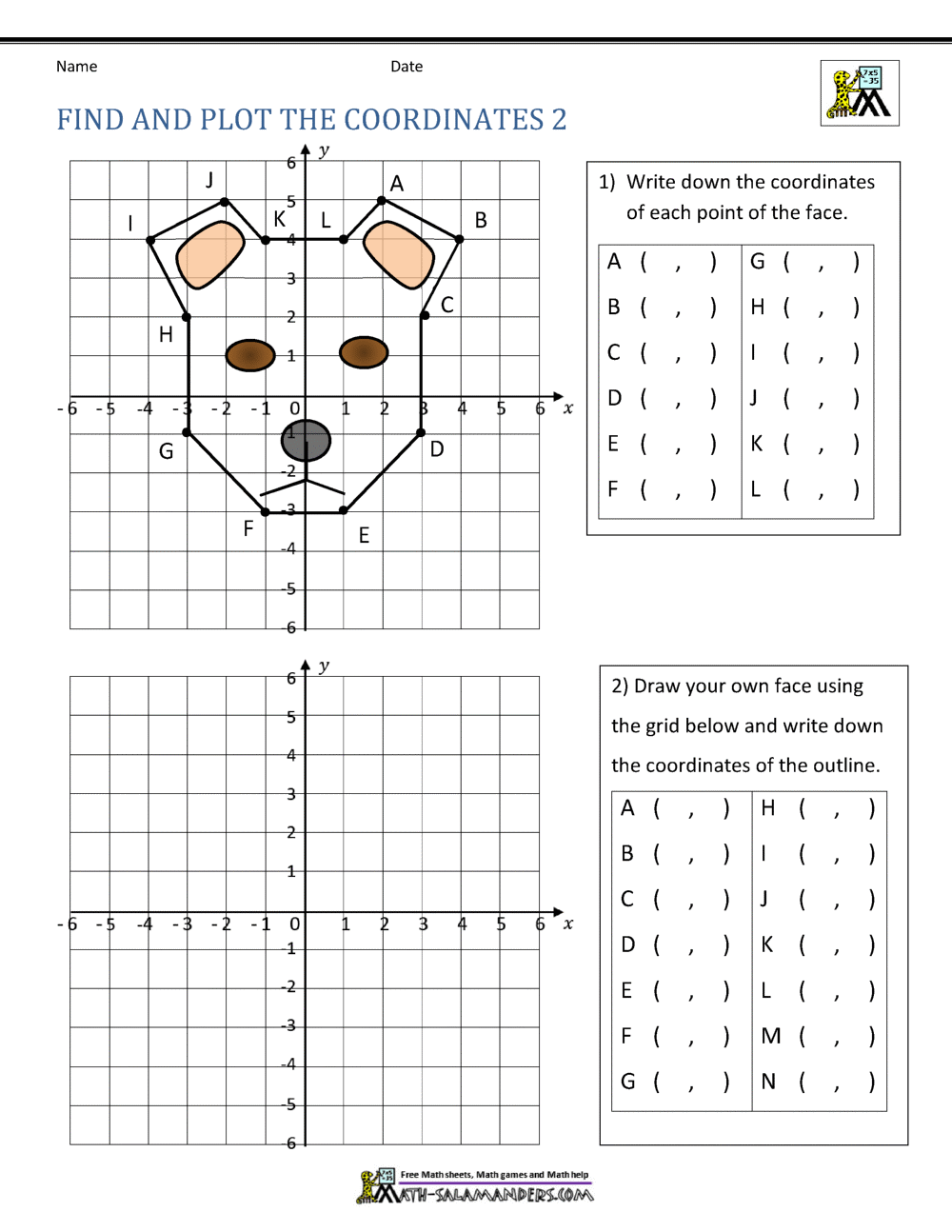
The coordinate plane, often referred to as the Cartesian plane, is a two-dimensional system where any point can be uniquely located by a pair of numbers known as coordinates. Here’s how it works:
- X-Axis: The horizontal line, representing the horizontal distance from the origin.
- Y-Axis: The vertical line, representing the vertical distance from the origin.
- Origin: The point where the X-axis and Y-axis intersect, marked as (0,0).
Each point on the plane is represented by an ordered pair (x, y), where:
- 'x' indicates the horizontal position or the distance along the X-axis.
- 'y' indicates the vertical position or the distance along the Y-axis.
📐 Note: Quadrants are labeled I, II, III, and IV, starting from the top right and moving counterclockwise.
Graphing Points
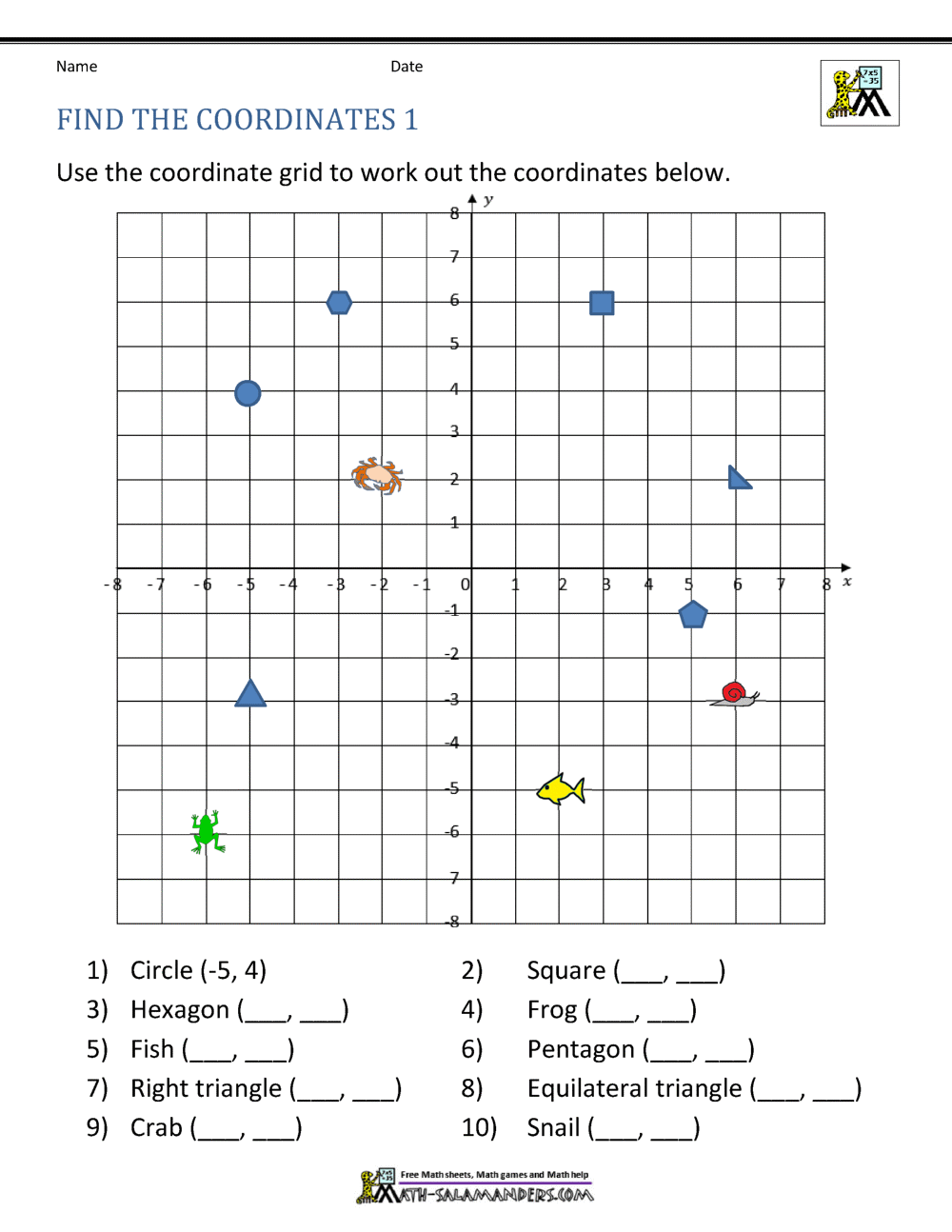
Here are the steps to graph points on the coordinate plane:
- Start at the origin: This is always (0, 0).
- Move horizontally: If the x-coordinate is positive, move right; if negative, move left.
- Move vertically: From the x-position, if the y-coordinate is positive, move up; if negative, move down.
- Mark the point: Use a dot to represent the coordinates.
📝 Note: Practice makes perfect. Consider using graph paper or coordinate plane paper to keep your lines straight and your points accurately placed.
Mastering Coordinate Plane Graphing

To excel in graphing on the coordinate plane, consider these techniques:
- Counting: Use finger counting or a small ruler for precision.
- Labeling: Always label your axes to understand the scale better.
- Using a Compass: For circular plots or parabolas, a compass can help in sketching perfect arcs.
- Paper Orientation: Rotate your paper if it helps visualize the graph better, especially for complex shapes.
Practical Applications

Understanding the coordinate plane extends beyond academic exercises. Here are some real-world applications:
| Application | Description |
|---|---|
| GPS Navigation | Uses latitude and longitude, which are essentially coordinates on Earth. |
| Computer Graphics | From video games to 3D modeling, objects are placed in a virtual coordinate space. |
| Land Surveying | Land is often mapped out with coordinates for property lines and planning. |

📱 Note: Modern technology relies heavily on coordinate systems. Many apps and devices use coordinates to enhance user experience, like location-based services or augmented reality.
The Printable Worksheet

To help you or your students practice graphing points on a coordinate plane, we’ve created a Printable Coordinate Plane Worksheet. Here’s how to use it:
- Download: [Link Removed]
- Print: Use standard 8.5 x 11 inch paper.
- Instructions: The worksheet contains several exercises ranging from plotting basic points to graphing lines and shapes.
📖 Note: Engage in regular practice. Consistency in practice will build both speed and accuracy in coordinate plane graphing.
The coordinate plane is an incredibly powerful tool for visualizing mathematical relationships. With the basics outlined above, you should now feel more confident in plotting points, understanding the structure of the coordinate plane, and seeing its practical applications. Remember, every great skill starts with foundational knowledge, and with practice, graphing on a coordinate plane will become second nature. Use the worksheet provided to refine your skills, and explore real-world applications to see how these mathematical principles come alive in everyday life. Keep practicing, and you'll find that the coordinate plane is not just a tool but a gateway to understanding and appreciating the beauty of mathematics.
Why do we use the coordinate plane?

+
The coordinate plane allows for precise plotting and analysis of data points, helping us visualize mathematical functions, patterns, and relationships in a two-dimensional space.
How do I know which quadrant a point is in?

+
Quadrants are numbered from I to IV starting in the upper right and moving counterclockwise. If both coordinates are positive, the point is in Quadrant I; positive x and negative y places it in Quadrant II, and so on.
What are some common mistakes when graphing on a coordinate plane?

+
Common mistakes include: reversing x and y coordinates, counting incorrectly, not labeling axes or scales, and misjudging distances. Regular practice and attention to detail can help avoid these errors.



