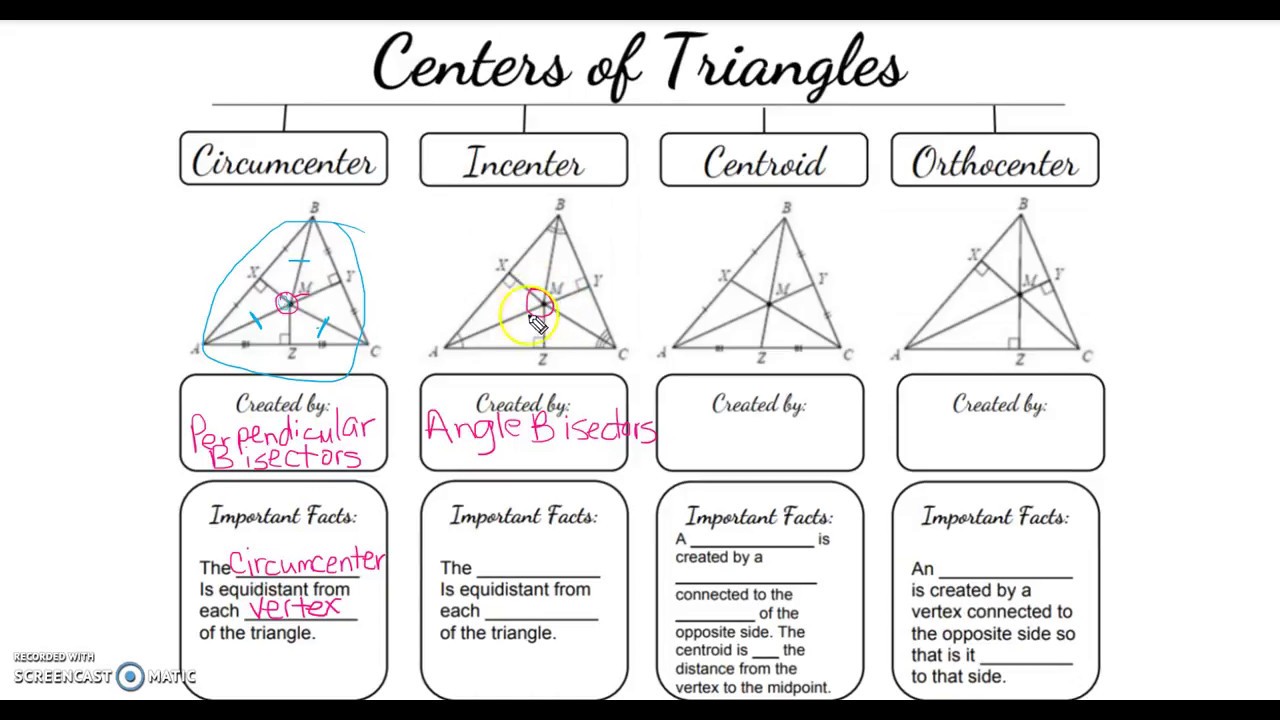
Triangle Centers Worksheet: Answer Key Revealed

The exploration of triangle centers is a fascinating journey into the heart of geometry, revealing the intrinsic properties and relationships among various points within a triangle. This article unveils an answer key to the Triangle Centers Worksheet, guiding you through triangle geometry, triangle properties, and triangle key points such as the centroid, orthocenter, circumcenter, and incenter. Each of these points holds unique significance in understanding the balance and symmetry within triangles. Let's delve into the details.
Understanding Triangle Centers

Before we dissect the worksheet, it’s crucial to understand what triangle centers are:
- Centroid - The point where the triangle’s medians intersect.
- Orthocenter - The intersection of the triangle’s altitudes.
- Circumcenter - The center of the circle that passes through all three vertices.
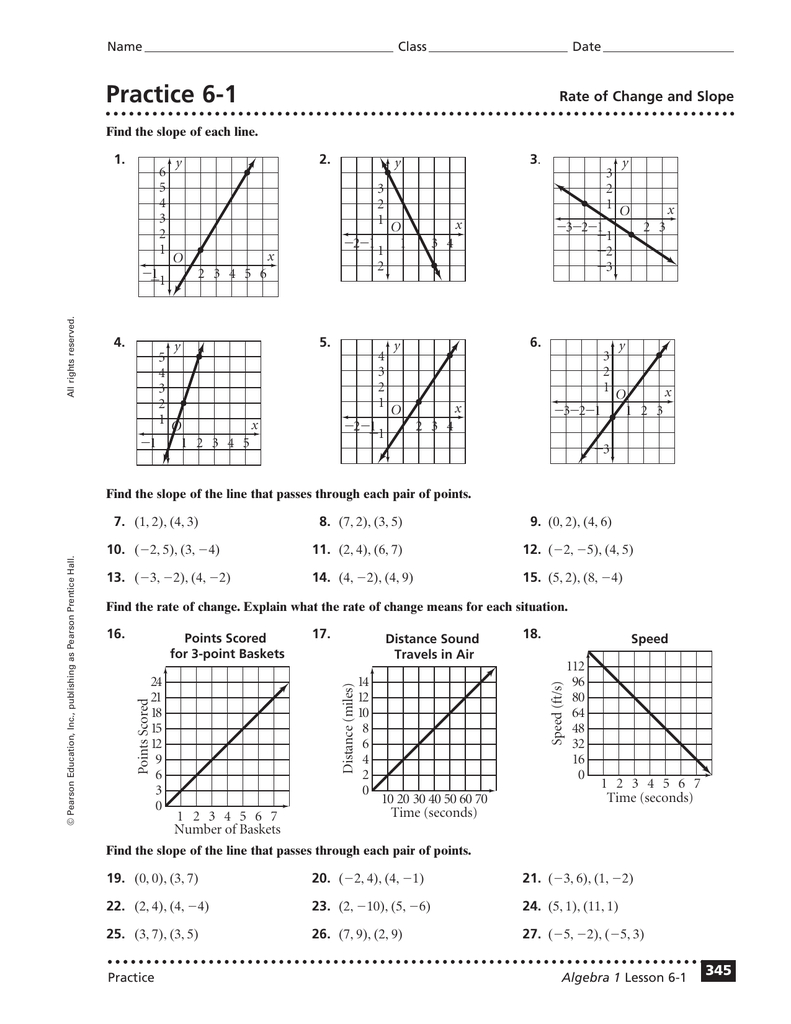
- Incenter - The point where the angle bisectors of the triangle meet.
Each center has unique properties that influence the triangle’s shape and symmetry.
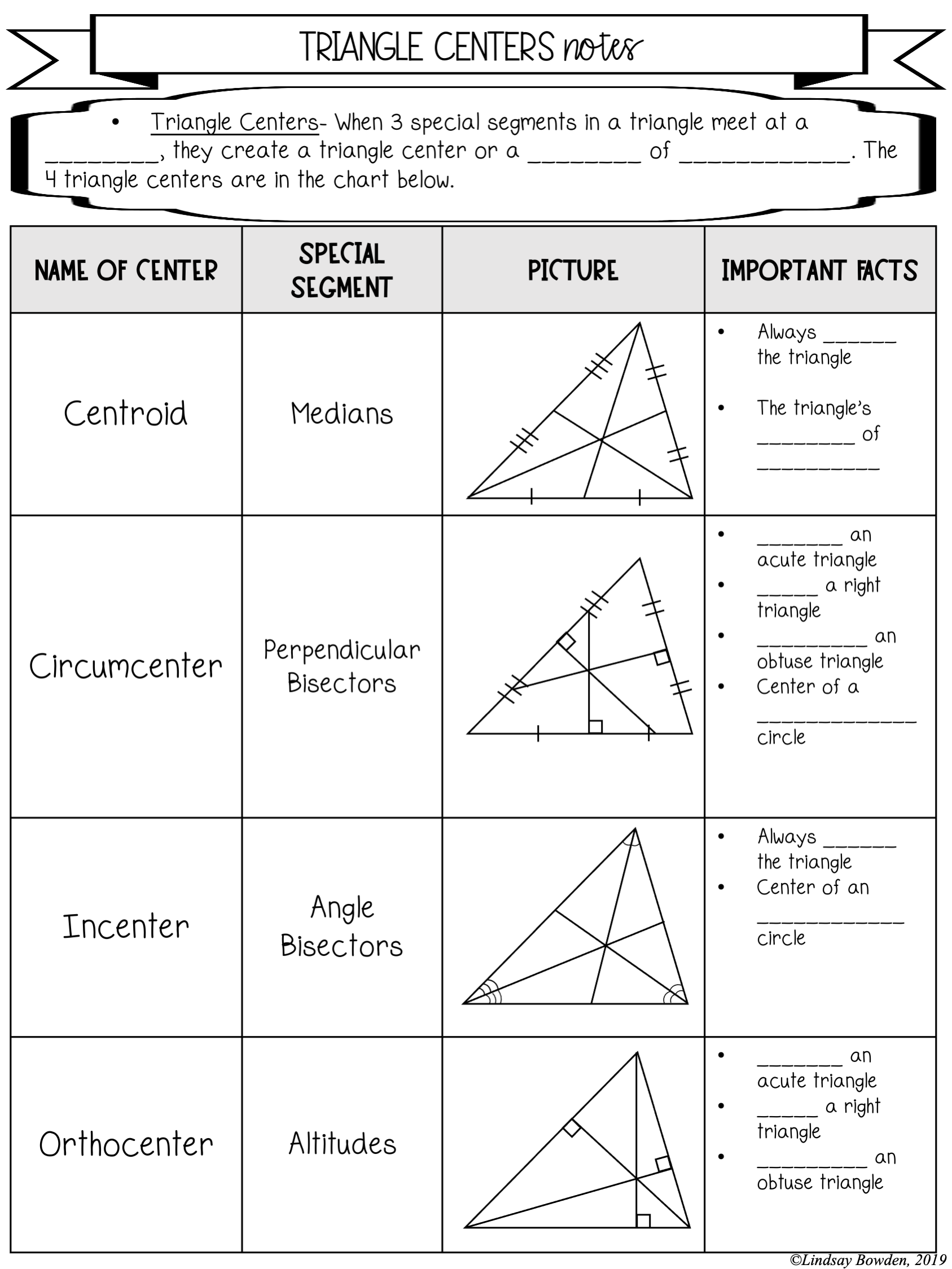
Centroid (G)
The centroid, often denoted as G, is the center of mass of a triangle. It divides each median into a ratio of 2:1. Here’s how to find it:
- Locate the midpoint of each side of the triangle.
- Draw lines from these midpoints to the opposite vertices. These are the medians.
- The intersection of these medians is the centroid.
⚠️ Note: The centroid is the only center that lies within all triangles, whether equilateral, isosceles, or scalene.
Orthocenter (H)
The orthocenter, labeled H, can lie inside, outside, or on the triangle:
- For an acute triangle, it is inside the triangle.
- In a right triangle, it coincides with the right angle vertex.
- For an obtuse triangle, it lies outside the triangle.
The orthocenter can be found by:
- Drawing the perpendiculars from each vertex to the opposite side (the altitudes).
- The intersection of these altitudes is the orthocenter.
🔍 Note: If any two altitudes are perpendicular, the triangle is a right triangle.
Circumcenter (O)
The circumcenter, represented by O, is equidistant from all three vertices of the triangle. Here’s how to locate it:
- Find the perpendicular bisectors of each side.
- The intersection of these bisectors gives you the circumcenter.
💡 Note: The circumcenter lies inside an acute triangle, on the hypotenuse of a right triangle, and outside an obtuse triangle.
Incenter (I)

The incenter, denoted as I, is the center of the triangle’s inscribed circle:
- Bisect each angle of the triangle.
- The intersection of these angle bisectors is the incenter.
📚 Note: The incenter always lies within the triangle, making it unique among the triangle centers.
Triangle Centers Worksheet Answer Key
This section provides a detailed answer key to the Triangle Centers Worksheet:
| Question | Answer |
|---|---|
| 1. Identify the centroid of a triangle with vertices at (0,0), (4,0), and (4,3). | The centroid is at (8/3, 1). |
| 2. For the same triangle, find the orthocenter. | Using trigonometry or vector calculus, the orthocenter is found at (-4, 12). |
| 3. What is the circumcenter of a triangle with vertices at (2,2), (4,6), and (8,4)? | The circumcenter is approximately (4.67, 3.33). |
| 4. Determine the incenter of the triangle described in question 3. | The incenter coordinates are approximately (4.24, 3.5). |

In summary

Through this comprehensive exploration, we’ve uncovered the intricate details of triangle centers, from the centroid’s role in mass distribution to the incenter’s significance in circle inscribing. Understanding these points not only enhances your appreciation of geometry but also equips you with tools to solve complex geometrical problems. The worksheet answers provided shed light on practical applications of these principles. As you continue your geometric journey, remember that the elegance of a triangle lies not just in its sides and angles but also in the special points that balance and connect them in unique ways.
What is the significance of the orthocenter in triangle geometry?

+
The orthocenter is significant because it is the common intersection of the triangle’s altitudes, providing insight into the triangle’s symmetry and the distribution of angles.
How do triangle centers relate to each other?

+
The centers of a triangle are related through Euler’s line, where the centroid, orthocenter, circumcenter, and sometimes the nine-point center all lie on this line, each in a specific ratio to the others.
Can the centroid be outside a triangle?
+
No, the centroid is always within the triangle, as it is the center of mass, dividing each median into segments with a 2:1 ratio.