GCF Monomials Worksheet: Master Simplifying Expressions Today
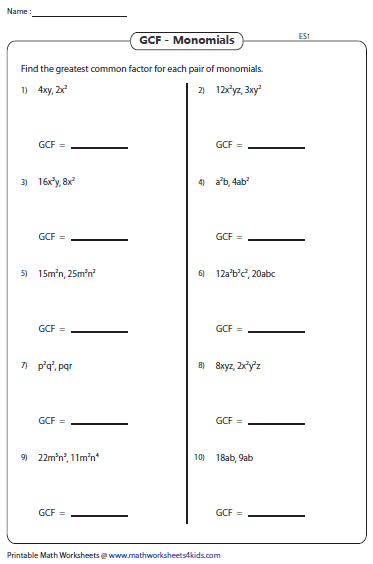
Monomials are a fundamental part of algebra, and understanding how to manipulate them is crucial for advancing in mathematics. Whether you're a student or a parent helping with homework, this guide on GCF (Greatest Common Factor) for monomials is crafted to provide a thorough understanding of simplifying expressions. Here, we'll dive into practical examples, techniques, and tips to make mastering this topic enjoyable and straightforward.
Understanding Monomials

A monomial is an algebraic expression consisting of a single term. It can include variables, coefficients, and constants, but multiplication or division by them is the only operation involved. For instance, 7xy or -9a3b are monomials.
Here are the key characteristics:
- Single Term: One term with no addition or subtraction.
- Variables: Can have one or more variables, each with an exponent.
- Co-efficient: A number that precedes the variables (optional).
Finding the Greatest Common Factor (GCF)

The GCF is the largest factor that two or more numbers or terms have in common. Here's how you find it:
- Numeric Factors: List all factors of each number, then identify the largest common factor.
- Variable Factors: For variables, the GCF is the lowest exponent that appears in all terms for that variable.

Applying GCF to Simplify Monomials

When you have a set of monomials:
- Identify the GCF of the numerical coefficients.
- Identify the lowest power of each variable common to all monomials.
- Factor out this GCF from each monomial to form a new term, leaving a remainder in parentheses.
Here's an example:
| Monomials | Operation | Result |
|---|---|---|
| 15x2, 12x3, 6x2 | GCF of 15, 12, and 6 is 3; Lowest power of x is x2 | 3x2 (5 + 4x - 2) |

💡 Note: When simplifying, ensure you multiply back to verify your work. This step helps catch any errors early on.
Tips for Mastery
- Practice, Practice, Practice: Consistent practice with varied examples will build your confidence.
- Understand the Concept: Don't just memorize steps; understand why each step is necessary.
- Organize Your Work: Keep your calculations neat to avoid confusion.
📝 Note: When working with algebraic expressions, always start with the basics like knowing how to find prime factors.
Next Steps

Now that you've seen how to simplify monomials using GCF, it's time to move forward. Here are some next steps to consider:
- Try different sets of monomials, increasing complexity.
- Explore further with polynomial expressions, applying the same GCF concept.
- Integrate this knowledge into more advanced topics like polynomial factoring.
Your journey through algebra will be much smoother as you master these techniques, making complex problems seem simple. As you practice, you'll discover the joy in the precision of math, where each step builds on the last, leading to a clear and satisfying resolution. Remember, the journey of mastering algebra isn't just about finding answers but also about understanding the 'why' and 'how' behind those answers.
What are the common mistakes when finding GCF of monomials?

+
Common mistakes include overlooking the lowest variable exponent, not factoring out the largest common factor, or mixing up addition and multiplication when simplifying expressions.
Can the GCF ever be 1?

+
Yes, when two or more monomials have no common variable or numeric factors, the GCF can indeed be 1, meaning the monomials are relatively prime or coprime to each other.
How do you factor monomials with negative coefficients?

+
Factor out the GCF as usual, but pay attention to signs. If all monomials have a common negative sign, factor out that sign with the GCF. For instance, with -12x2 and -18x, you can factor out -6x to get -6x(2x-3).