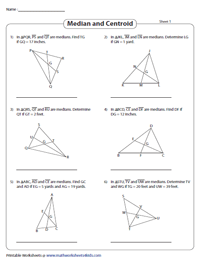
Triangle Centers Worksheet: Simplify Geometry Now

In the field of geometry, understanding various centers within triangles is essential for both students and enthusiasts. These centers, such as the centroid, orthocenter, circumcenter, and incenter, each provide unique insights into the properties and behaviors of triangles. This post aims to delve deeply into these triangle centers, offering clear explanations, illustrative examples, and practical advice on how to identify and apply these concepts in real-world scenarios.
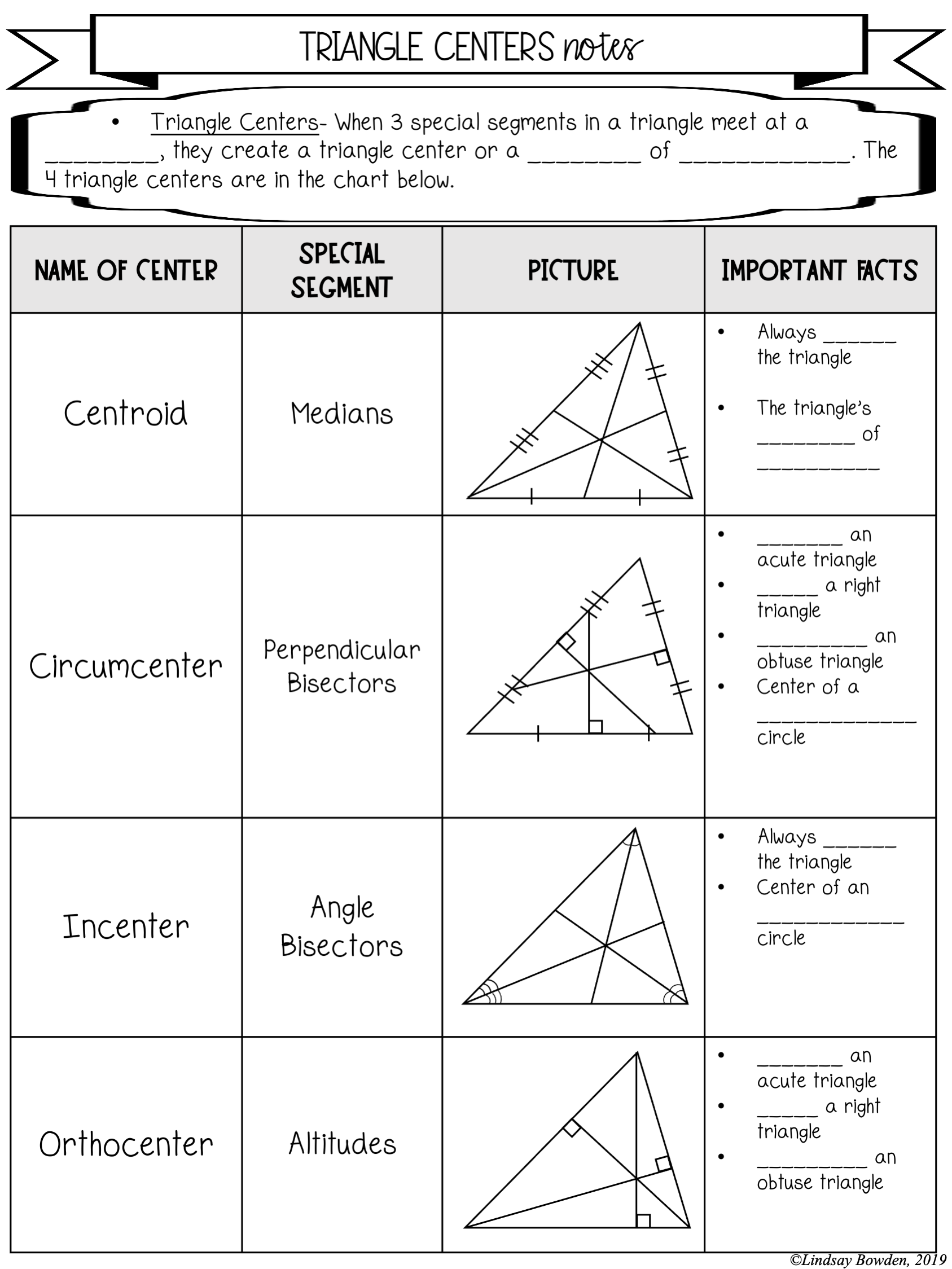
Introduction to Triangle Centers

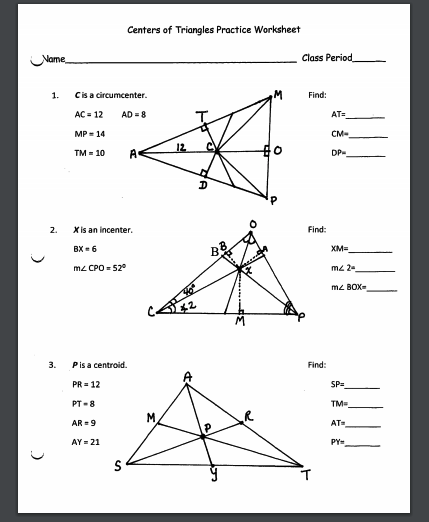
Triangle centers are specific points within a triangle that hold special properties or symmetry. Here are the primary triangle centers:
- Centroid: The point where the medians of a triangle intersect.
- Orthocenter: The point where the altitudes of a triangle intersect.
- Circumcenter: The center of the circle that circumscribes the triangle.
- Incenter: The center of the circle that inscribes the triangle.

📘 Note: While these centers are usually distinct in a non-equilateral triangle, they coincide in an equilateral triangle.
The Centroid
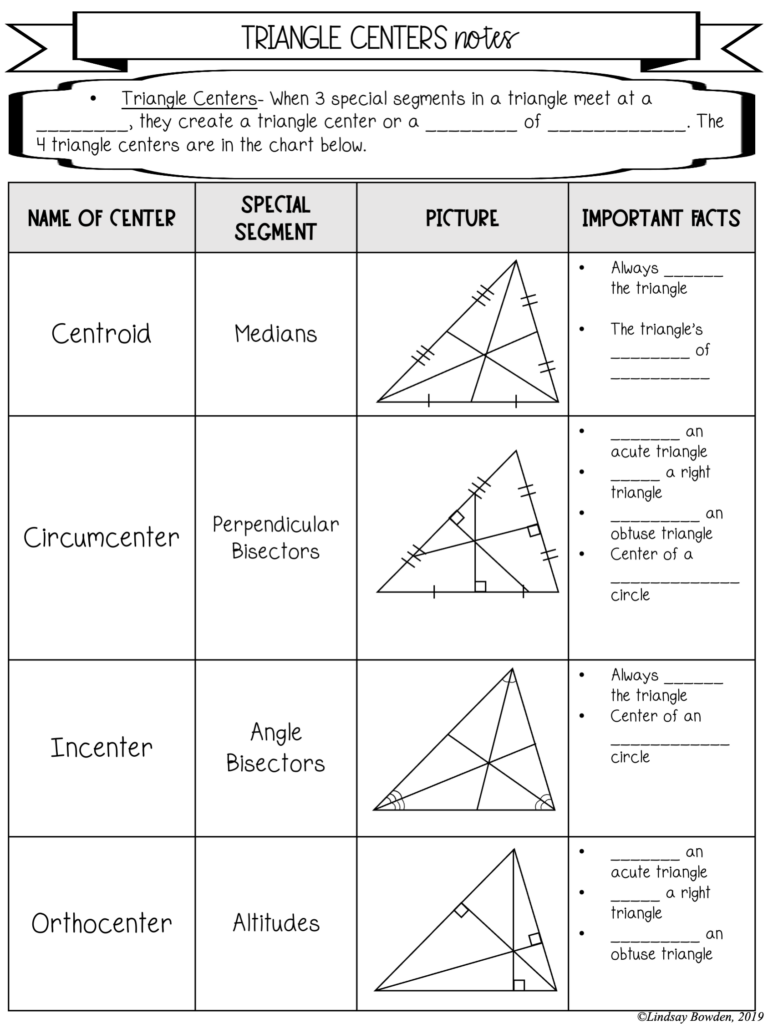
The centroid of a triangle is often referred to as the "balance point". Here's what you need to know about the centroid:
- It divides each median into a ratio of 2:1 (with the longer segment closer to the vertex).
- To find the centroid, you can use the formula:
Coordinates Formula xG (x1 + x2 + x3)/3 yG (y1 + y2 + y3)/3 

💡 Note: The centroid is also known as the "mass center" if the triangle's mass is uniformly distributed.
The Orthocenter
The orthocenter of a triangle is the convergence point of the perpendiculars dropped from the vertices to the opposite sides:
- In an acute triangle, it lies inside the triangle.
- In an obtuse triangle, it lies outside.
- In a right triangle, it is located at the vertex with the right angle.

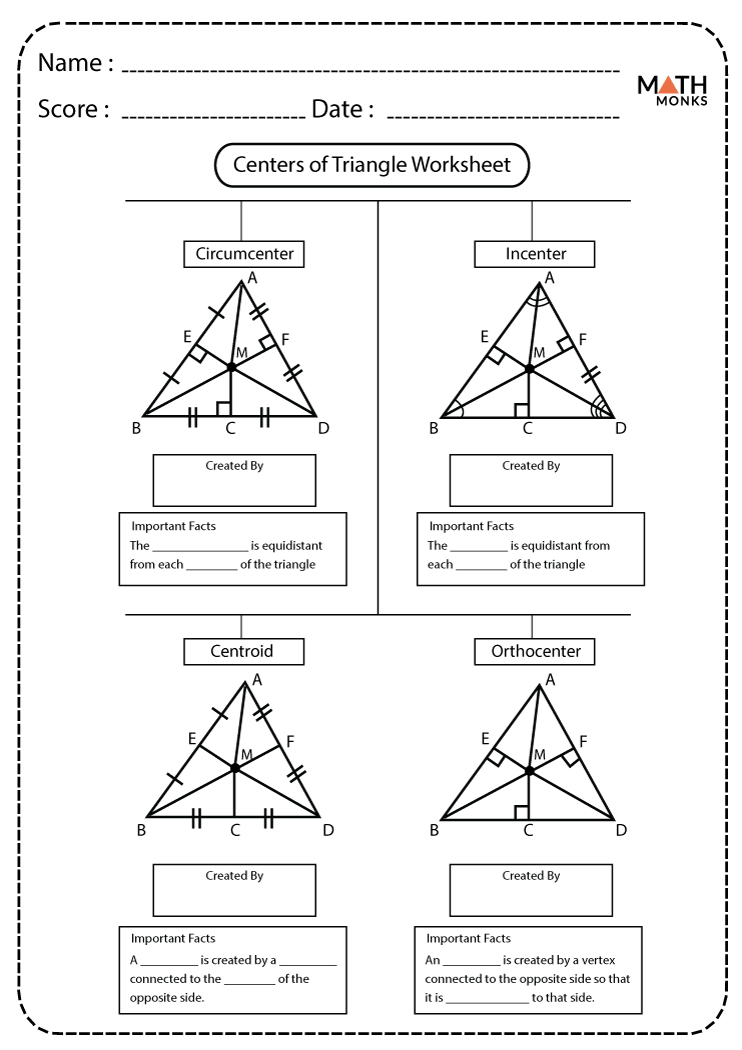
The Circumcenter

The circumcenter is equidistant from all vertices of the triangle:
- The circumradius (R) can be calculated using the following formula:
Formula Description R = \frac{a}{2 \sin A} a - side length opposite angle A - In an isosceles triangle, the circumcenter lies on the perpendicular bisector of the base.

📚 Note: The circumcenter's position can be inside, on, or outside the triangle, depending on the type of triangle.
The Incenter
The incenter is where the angle bisectors of the triangle intersect:
- It is always inside the triangle.
- The inradius (r) can be calculated using:
Formula Description r = \frac{A}{s} A - area, s - semiperimeter - The incenter has the property that the sum of its distances to the sides equals the triangle's perimeter.

Real-World Applications of Triangle Centers

The study of triangle centers has practical applications in:
- Architecture: Understanding structural stability and load distribution.
- Surveying: Triangulation methods for mapping terrain.
- Graphics: Computer graphics for rendering complex shapes.
🚧 Note: Triangle centers play a crucial role in understanding and optimizing load distribution in truss systems.
In summary, understanding triangle centers not only enhances one's appreciation for geometric intricacies but also provides foundational knowledge for various real-world applications. Whether you are analyzing the stress points in a bridge or designing an intricate piece of art, these centers offer insights into the properties of triangles that are both fundamental and fascinating.
What is the significance of the incenter in practical applications?

+
The incenter is critical in applications where uniformity in distances from a point to the sides of a shape is needed, such as in design or where equal access to different parts of a structure is desired.
Can you simplify how to find the circumcenter for non-mathematical minds?
+
Think of the circumcenter as the point you would use to perfectly center a circular dish around your triangle. It’s the middle point where all sides would touch a circle drawn around the triangle.
Why do these centers matter in engineering?
+
Engineers use these centers to understand and predict how forces will distribute in triangular structures. Knowing where these centers are helps in designing stable and efficient structures.
How can someone use these centers in everyday life?

+
In practical terms, knowing these centers can help in cutting materials evenly, designing stable furniture, or even understanding why a certain shape feels balanced or unbalanced.