5 Tips for Mastering Medians and Centroid Worksheet
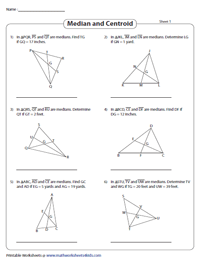
Calculating medians and centroids in geometry isn't just a vital part of the curriculum; it's a gateway to understanding the intricate balance and symmetry within geometric shapes. If you're finding this topic challenging, here are five comprehensive tips to help you master the art of working with medians and centroids, especially when tackling those tricky worksheets.
Understanding Medians and Centroids

Before diving into tips, let’s solidify the definitions:
- Median - A line segment joining a vertex of a triangle to the midpoint of the opposite side.
- Centroid - The point where all three medians of a triangle intersect. It’s also known as the triangle’s geometric center.

Tip 1: Visualize Before You Solve
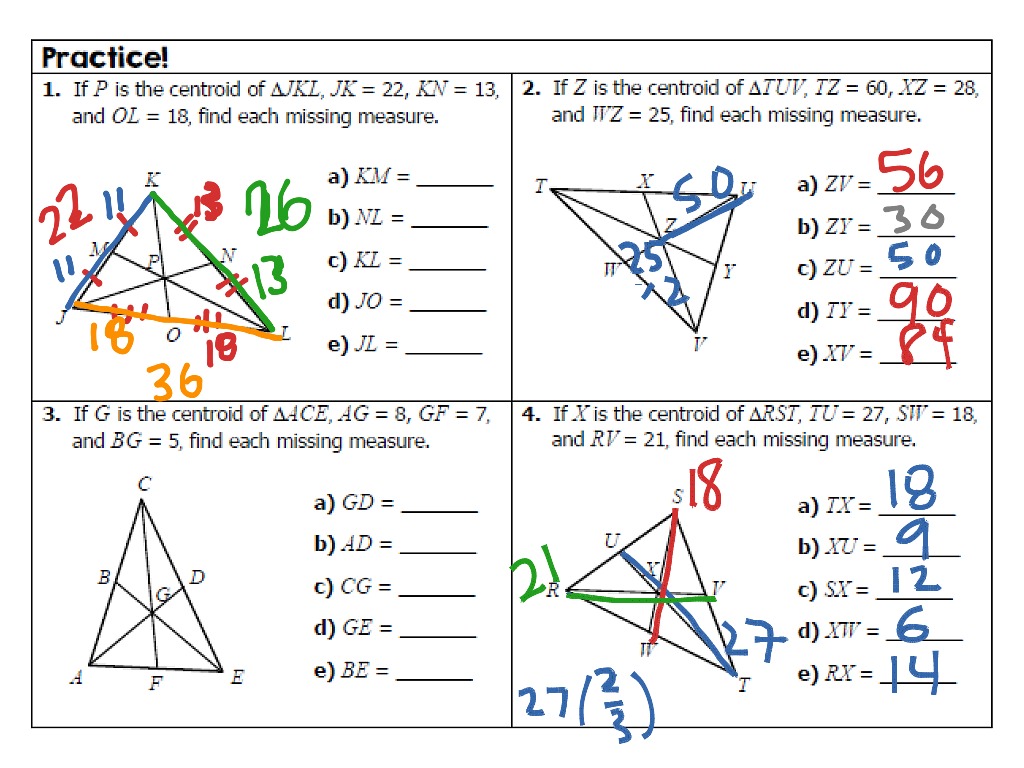
One of the most effective strategies for understanding and solving problems involving medians and centroids is to visualize the shape:
- Draw your triangle and sketch the medians. Seeing where they intersect in the middle is a direct representation of the centroid.
- Use different colors for each median to keep track of the lines. This can also help in understanding the symmetry.
Tip 2: Use the Formulas to Your Advantage

Formulas aren’t just for calculation; they can guide your understanding:
| Property | Formula |
|---|---|
| Length of a Median | ( \sqrt{ \frac{2b^2 + 2c^2 - a^2}{4} } ) |
| Centroid Division | The centroid divides each median into a ratio of ( 2:1 ). |

By understanding these formulas, you can anticipate the values you're likely to work with when solving problems.
Tip 3: Practice with Diverse Triangle Types

Not all triangles are created equal, so practice with:
- Equilateral triangles where all sides are equal, and the centroid is also the circumcenter, orthocenter, and incenter.
- Isosceles triangles where two sides are equal, simplifying calculations.
- Scalene triangles with no sides equal, which require full calculations.
✍️ Note: Real-world problems might not specify the triangle type, so being versed in all types is key.
Tip 4: Apply Real-World Context

Understanding how these geometric concepts apply in real life can make the subject less abstract:
- In architecture, architects calculate the centroid of structures to find the center of gravity for stability.
- In mechanical engineering, centroids help in designing parts that will resist rotational forces uniformly.
- Physics uses centroids to determine the balance point of objects, crucial for stability and motion studies.
Linking theory to practical examples can enrich your understanding and retention.
Tip 5: Use Technology to Verify Your Work

While nothing replaces understanding, leveraging technology can:
- Help in visualizing complex problems through dynamic geometry software like GeoGebra.
- Verify your calculations through math tools like WolframAlpha, ensuring accuracy.
- Serve as an interactive tutor with educational apps like Desmos, which can simulate real-time geometric constructions.
Remember, while technology is a fantastic tool, understanding the ‘why’ behind your work is still paramount.
To sum up, mastering medians and centroids involves visualization, a grasp of formulas, diverse practice, real-world application, and technological support. Integrating these tips can significantly enhance your geometric skills. Keep practicing, and remember that each worksheet is a step towards a deeper understanding of the elegance and balance within geometry.
What are the advantages of understanding medians and centroids?

+
Understanding medians and centroids provides insights into the symmetry, balance, and stability of triangles. This knowledge is crucial in various fields like architecture, engineering, physics, and computer graphics, where understanding the center of mass is vital for design and functionality.
How can one practice finding centroids effectively?

+
Effective practice involves working with different types of triangles, using dynamic geometry software for real-time visualization, and applying the concepts to real-world scenarios. Additionally, using physical models or interactive simulations can enhance understanding.
Is there a quick way to calculate the centroid without complex formulas?

+
In simple terms, if you draw any triangle and connect each vertex to the midpoint of the opposite side, the point where these lines meet is the centroid. However, for precise calculations, using the formula or a graphing calculator can be beneficial, especially for complex triangles or in professional applications.