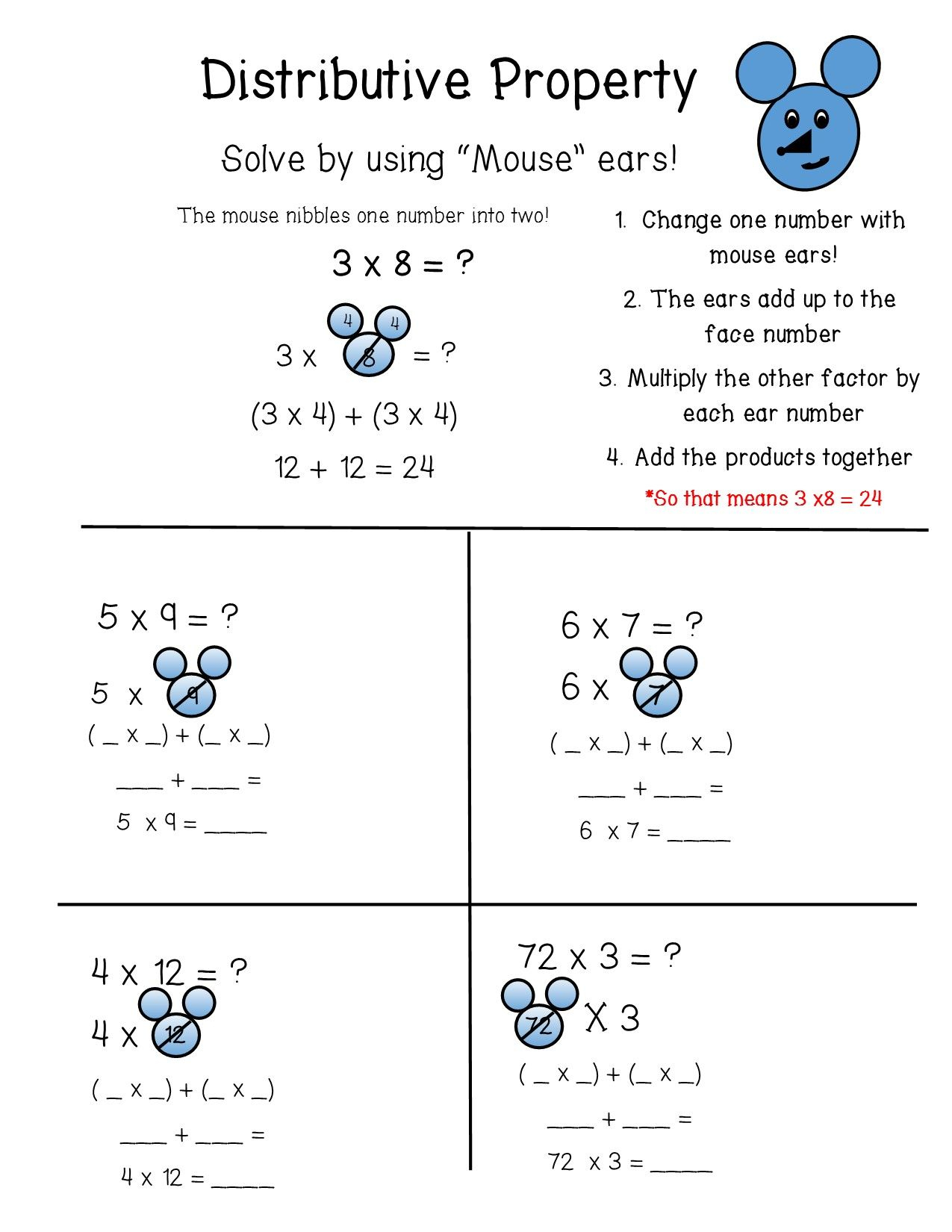
5 Ways to Master Multiplication Using Distributive Property

The distributive property in mathematics is a valuable tool that simplifies multiplication problems by breaking them down into more manageable pieces. It states that a(b + c) = ab + ac, which means you can multiply a sum by multiplying each addend separately and then adding the products. This principle isn't just a mathematical trick; it can be a strategy to master multiplication. Let's explore five methods to harness the power of the distributive property to simplify your calculations and enhance your mathematical fluency.
Method 1: The Building Block Approach

The first step to mastering multiplication through the distributive property is to understand how numbers are composed. Here’s how you can use it:
- Break Down Numbers: If you have to multiply 12 by 6, break 12 into 10 and 2. Now multiply each part by 6: 10 * 6 = 60, 2 * 6 = 12, and then add: 60 + 12 = 72.
- Use Units Digit: Sometimes, multiplying by the units digit can be easier. For example, 13 * 7 can be visualized as (10 * 7) + (3 * 7) = 70 + 21 = 91.
💡 Note: This method is particularly useful when one of the numbers to multiply has a units digit you are familiar with or can easily multiply.
Method 2: Re-ordering Factors

Sometimes, re-arranging the factors of multiplication can make the problem easier:
- Factor into Prime Factors: Breaking down the numbers into their prime factors can make multiplication simpler. For instance, 28 * 5 can be seen as 4 * 7 * 5, where you can re-order to make 5 * 4 * 7, which becomes 20 * 7 = 140.
- Re-associate Factors: If you have 6 * 5 * 14, you can re-associate: (6 * 5) * 14 = 30 * 14. Now, use the distributive property: (30 * 10) + (30 * 4) = 300 + 120 = 420.
Method 3: Partial Products

This method involves breaking one factor into smaller parts and multiplying them separately:
- Multiply in Parts: Let’s say you want to multiply 47 by 8. Think of 47 as 40 + 7. Now, 40 * 8 = 320, 7 * 8 = 56, and 320 + 56 = 376.
- Add Multiplicative Ease: For example, 18 * 9 can be seen as (10 * 9) + (8 * 9) = 90 + 72 = 162.
| Expression | Calculation | Result |
|---|---|---|
| 47 * 8 | (40 * 8) + (7 * 8) | 376 |
| 18 * 9 | (10 * 9) + (8 * 9) | 162 |

Method 4: Mental Arithmetic Aid

The distributive property is a powerful ally in mental arithmetic:
- Visualize Numbers: When faced with a multiplication like 15 * 14, think 10 * 14 = 140, 5 * 14 = 70, and then sum them up: 140 + 70 = 210.
- Link to Known Facts: If you know that 12 * 5 = 60, you can easily find 13 * 5 by adding 5 more: 60 + 5 = 65.
Method 5: Distributive Property in Polynomials
While these methods are beneficial for arithmetic, the distributive property extends its power to algebraic expressions:
- Simplify Multiplication: Use the property to distribute factors over sums or differences. For example, a(b + c) = ab + ac.
- Example: If you need to multiply (2x + 3) by 4, think 4 * 2x = 8x, 4 * 3 = 12, so (2x + 3) * 4 = 8x + 12.
In conclusion, the distributive property is not just a concept to memorize; it's a strategy for enhancing calculation speed, precision, and comprehension. By applying the methods outlined above, you can conquer complex multiplication problems and gain a deeper understanding of the interconnected nature of numbers. With practice, the use of the distributive property becomes second nature, fostering a more intuitive approach to problem-solving. Remember, the beauty of math lies in its ability to simplify complex concepts into fundamental truths, allowing us to see the elegance in the simplicity of multiplication.
Why should I bother learning the distributive property?

+
Learning the distributive property helps in simplifying calculations, understanding algebraic expressions, and aids in mental arithmetic, making it a fundamental tool for mathematical fluency.
Can the distributive property be used with subtraction?

+
Yes, the distributive property can be applied to subtraction as well. For instance, a(b - c) = ab - ac.
How does the distributive property help in algebraic simplification?

+
It helps in breaking down expressions into simpler components, making it easier to multiply or factor out terms, especially when dealing with polynomials.