Box And Whisker Plot Worksheets

Introduction
Understanding data is crucial in today's world, where information drives decision-making across various fields. One effective tool for visualizing data distribution is the box and whisker plot, or simply box plot. These plots allow analysts and researchers to summarize sets of numerical data in a visually intuitive manner. Here, we'll delve into how you can learn to create and interpret box plots through worksheets tailored for all skill levels.
Understanding Box and Whisker Plots
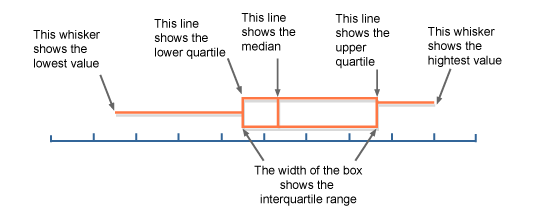
A box and whisker plot provides a five-number summary of a data set:
- The minimum value
- The first quartile (Q1)
- The median (Q2 or 50th percentile)
- The third quartile (Q3)
- The maximum value
These plots help in:
- Identifying the median and quartiles quickly
- Visualizing the skewness or symmetry of the data
- Spotting outliers easily
- Comparing distributions of different data sets
Components of a Box Plot
Here's a breakdown of what each part of the box plot represents:
| Component | Description |
|---|---|
| Box | Encloses the middle 50% of the data from Q1 to Q3. |
| Whiskers | Extend from the box to the minimum and maximum values within 1.5 * IQR (Interquartile Range) from Q1 or Q3. |
| Outliers | Any point outside the whiskers, often represented by dots or asterisks. |

Using Worksheets to Master Box Plots

Worksheets can be an excellent tool for mastering the creation and interpretation of box and whisker plots. Here's how you can approach learning:
Beginner Level Worksheets

- Creating Simple Box Plots: Start with data sets that are easy to calculate quartiles and identify outliers. Practice plotting these manually on graph paper or using software.
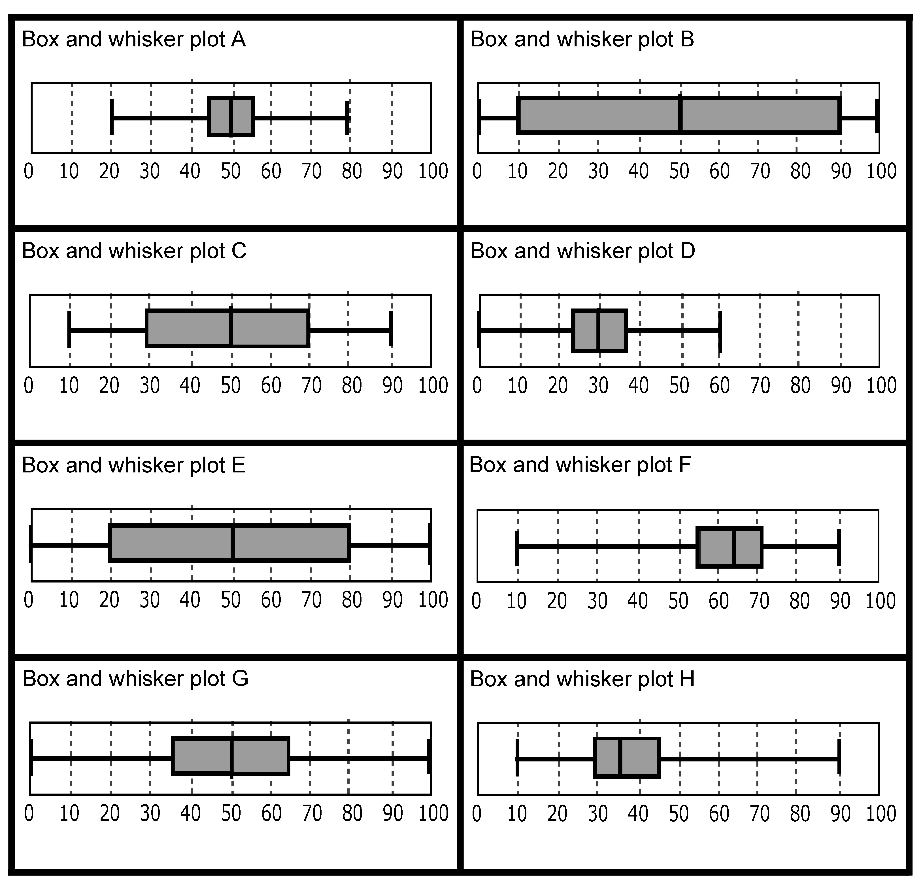
- Interpretation Exercises: Given box plots, identify the five-number summary, determine the range and interquartile range, and analyze for skewness.
📊 Note: Start with data sets with a small number of values to minimize calculations.
Intermediate Level Worksheets

- Box Plot Analysis: Work with larger data sets, including those with potential outliers. Use these to understand how box plots handle extreme values.
- Multiple Box Plot Comparison: Compare distributions from different samples or groups to understand variability and central tendencies.
📊 Note: Remember to consider the scale when comparing box plots from different sets to avoid misleading conclusions.
Advanced Worksheets

- Real-World Applications: Use data from real-world sources like finance, health statistics, or weather patterns to create box plots and discuss implications.
- Software Usage: Utilize tools like Excel, SPSS, R, or Python to automate box plot creation and enhance your data analysis skills.
- Variations in Box Plots: Explore variations like notched box plots to understand how different configurations reflect statistical nuances.
Tips for Effective Learning
- Consistency is Key: Regular practice helps in better retention of concepts.
- Use Technology: Software tools can provide a dynamic learning experience.
- Review and Correct: Check your work against the given solutions to understand your mistakes.
- Collaborate: Discuss your findings and methods with peers to gain new insights.
By following these steps, you'll develop a profound understanding of how to interpret and construct box plots, enhancing your data analysis skills significantly.
In summary, box and whisker plots are indispensable tools in statistics for summarizing and visualizing data distribution. Through carefully designed worksheets, learners can grasp the fundamentals and intricacies of box plots. From understanding basic components to advanced real-world applications, these exercises help transform raw data into insightful stories.
What does the length of the whiskers indicate in a box plot?

+
The length of the whiskers in a box plot shows the range of the data within 1.5 times the interquartile range (IQR) from the first and third quartiles. Longer whiskers indicate a wider spread or higher variability in the data.
How can I identify outliers using a box plot?

+
Outliers in a box plot are typically represented by points or asterisks outside the whiskers. They are any data points beyond 1.5 * IQR from the box (Q1 or Q3).
Why are box plots useful for comparing distributions?

+
Box plots provide a visual summary of the distribution, central tendency, and variability of data sets. By aligning multiple box plots, you can quickly compare medians, quartiles, and the presence or extent of outliers, offering a clear picture of how different groups or samples differ.
Can I use a box plot for categorical data?

+
Yes, box plots can be adapted for categorical data by creating separate plots for each category, allowing for comparison across categories.
How does skewness show up in box plots?

+
In a box plot, skewness is indicated by an asymmetry in the distribution. If the median is closer to the bottom of the box, the data is positively skewed, and if closer to the top, it’s negatively skewed. Additionally, if one whisker is longer than the other, it further suggests skewness.


