5 Easy Tips for Mastering Equivalent Fractions

Fractions can be a tricky concept for many, but mastering equivalent fractions is key to understanding more complex mathematical concepts. Equivalent fractions are fractions that represent the same value, even though they might look different at a glance. Here, we will explore five easy tips to help you, or your students, become experts in this fundamental aspect of mathematics.
1. Understand the Basics
Before diving into the nuances of equivalent fractions, it's crucial to grasp the basic concepts of fractions. A fraction is made of a numerator (the top number) which indicates the part you're considering, and a denominator (the bottom number) which indicates the whole that the numerator refers to. When these two numbers change but their ratio remains the same, you get equivalent fractions.
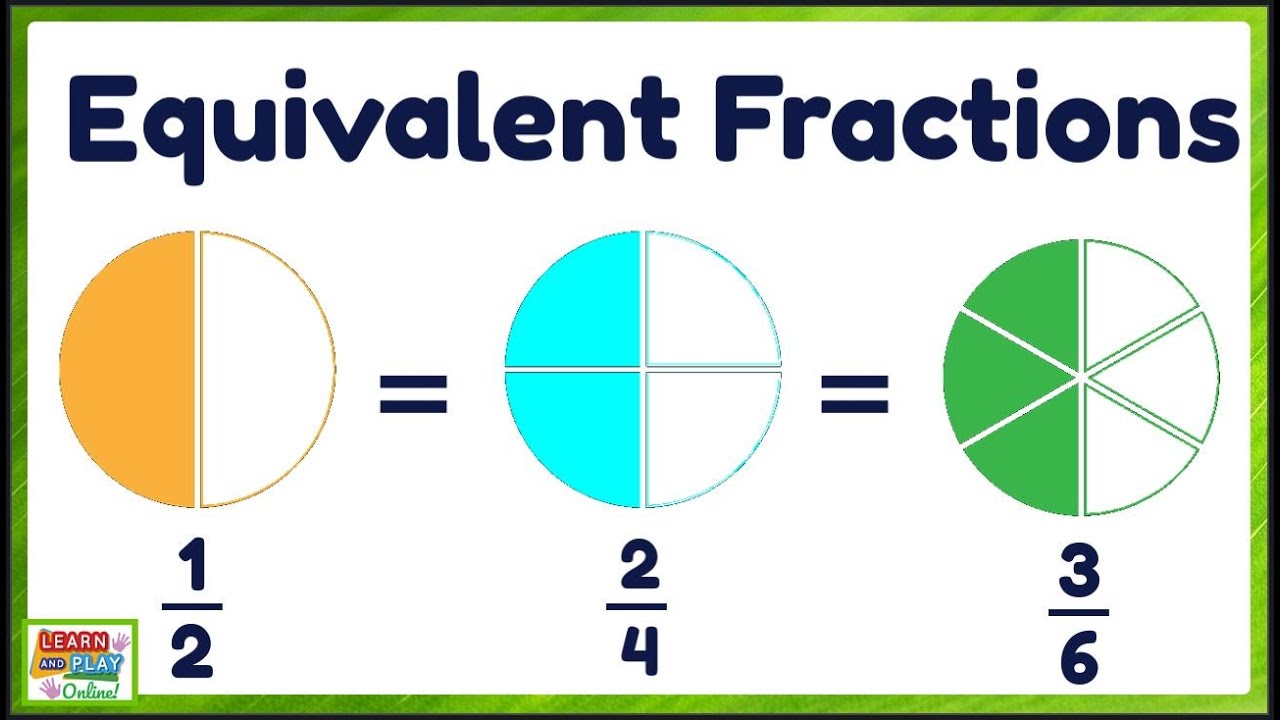
- Definition: Equivalent fractions are fractions that have different numerators and denominators but are equal in value.
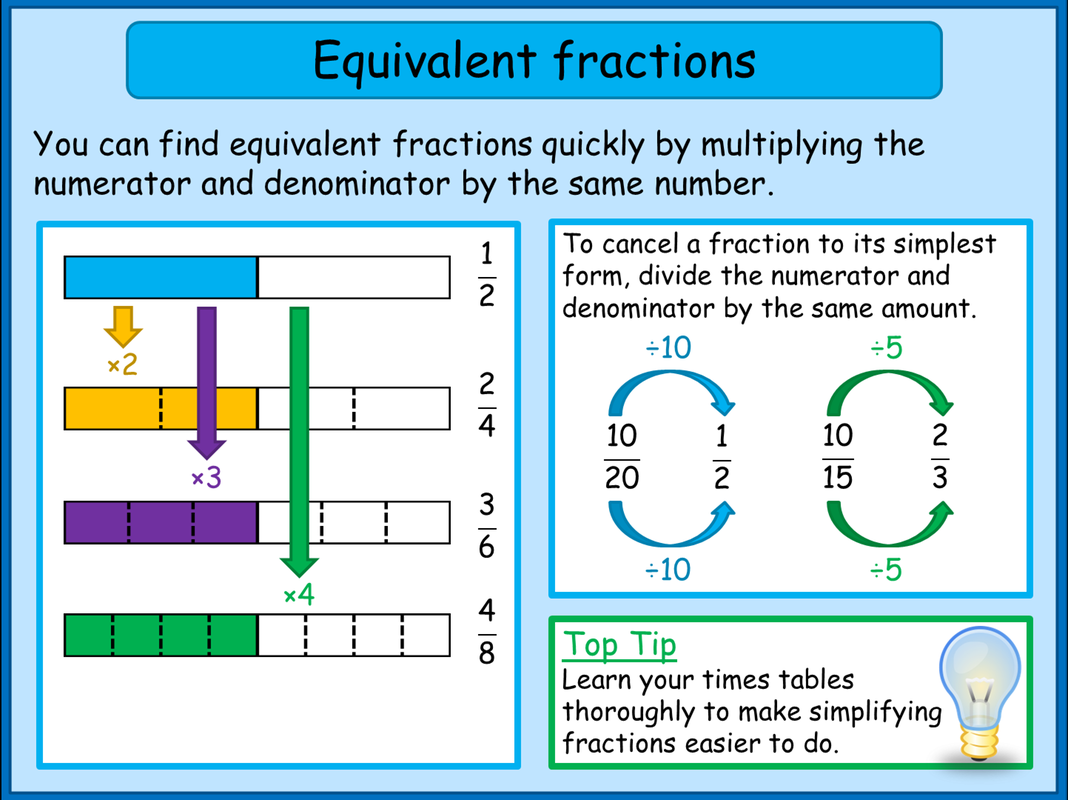
- Example: 1/2 is equivalent to 2/4, 3/6, or 5/10.
2. Use Multiples

One of the simplest ways to find equivalent fractions is by multiplying or dividing both the numerator and the denominator by the same number. This process doesn't change the value of the fraction because you're essentially dividing or multiplying the whole by the same factor.
- To make larger fractions, multiply both the numerator and the denominator by a factor.
- Conversely, to create smaller fractions, you can divide both the numerator and the denominator by the same factor.
💡 Note: Always multiply or divide by the same number to ensure the fractions remain equivalent.
3. Master the Cross-Multiplication Technique
The cross-multiplication method is not just useful for comparing fractions but also for finding equivalent ones. Here's how to use it:
- Write down the two fractions next to each other, ensuring one fraction is on the left, the other on the right.
- Cross-multiply the numerators with the denominators of the other fraction.
- If the products are equal, the fractions are equivalent.

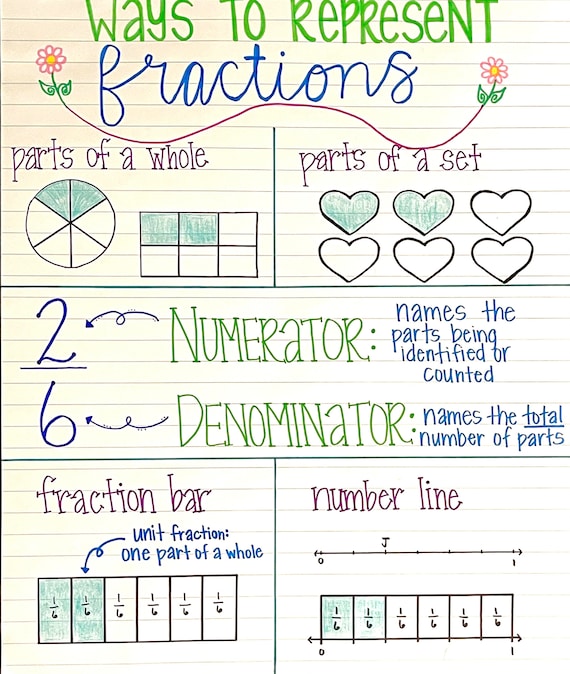
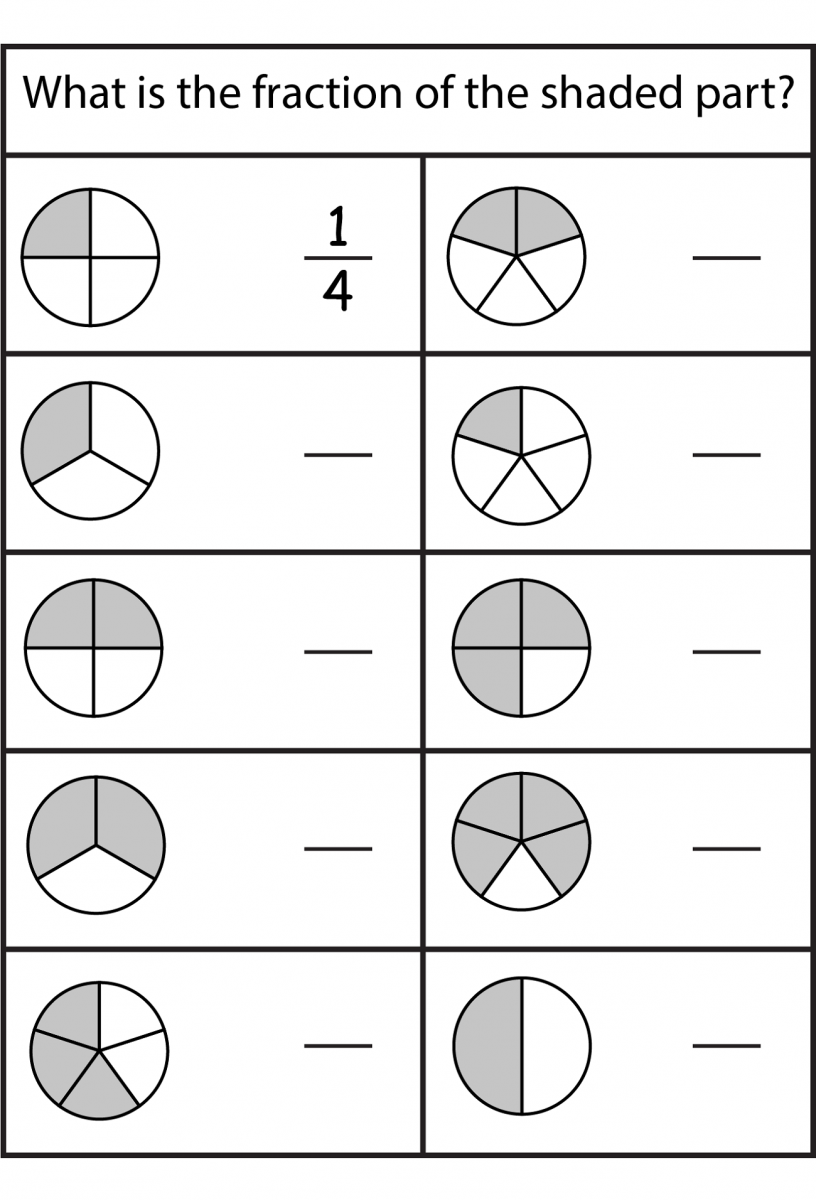
4. Practice with Visual Representations
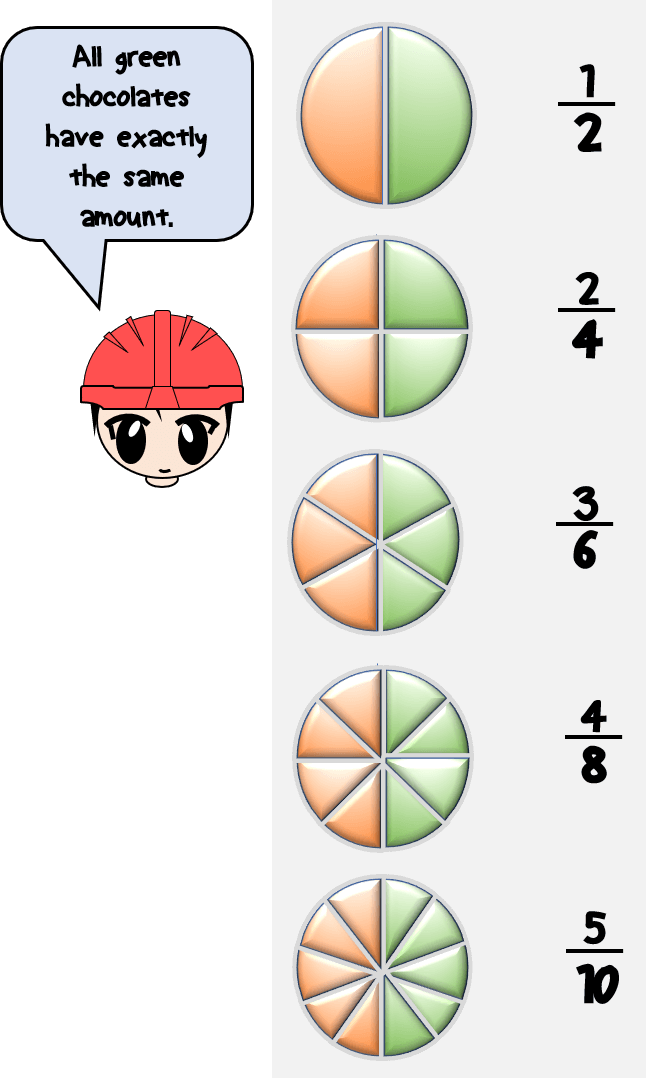
Visual aids can be extremely helpful for understanding equivalent fractions. Here's how you can use them:
- Use shapes or pies to visually divide and show equivalent parts.
- Employ number lines to plot fractions and see how they relate to each other.
- Utilize fraction bars or other manipulative materials to physically show the equivalence of different fractions.
| Original Fraction | Equivalent Fractions | Visual Representation |
|---|---|---|
| 1/2 | 2/4, 3/6, 4/8 | A circle cut into two halves, showing equivalent parts of 1/2, 2/4, 3/6, and 4/8. |
| 1/3 | 2/6, 3/9, 4/12 | A circle cut into three equal parts, showing how 1/3 relates to 2/6, 3/9, and 4/12. |
📝 Note: Visual aids can particularly benefit visual learners, helping them to grasp concepts more easily.
5. Embrace Simplification
When dealing with equivalent fractions, knowing how to simplify them is just as important. Simplifying involves dividing both the numerator and the denominator by their greatest common divisor (GCD):
- Step 1: Find the GCD of the numerator and the denominator.
- Step 2: Divide both the numerator and the denominator by the GCD.
- Step 3: Repeat until the fraction cannot be simplified further.
🔎 Note: Simplifying fractions doesn't change their value but makes them easier to work with and understand.
Mastering equivalent fractions is not just about memorizing formulas or techniques; it's about understanding the underlying principles of how fractions work. With these five easy tips, you or your students can approach equivalent fractions with confidence, opening the door to more advanced mathematical understanding and proficiency. Remember, the key to mastering any mathematical concept lies in consistent practice and a deep conceptual understanding of the subject.
Why are equivalent fractions important?
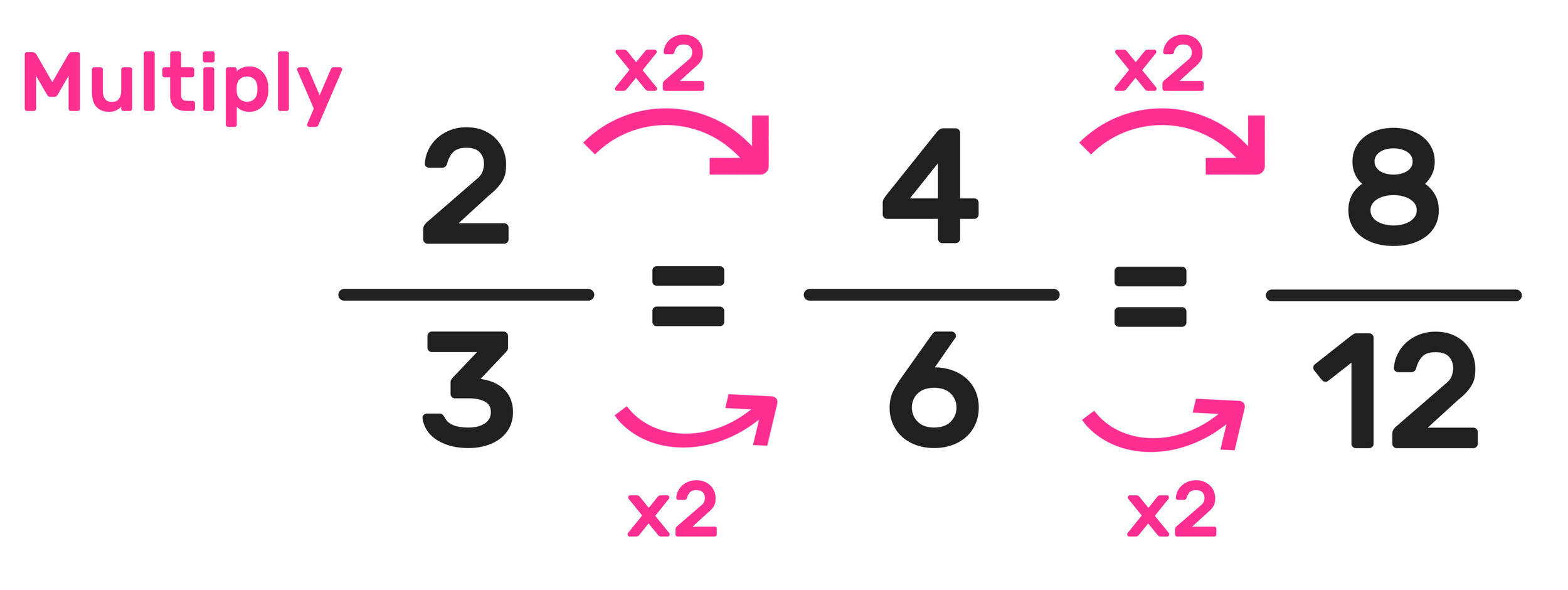
+
Equivalent fractions help in comparing, adding, subtracting, and understanding fractions in different contexts, making complex math operations easier to solve.
Can a fraction be equivalent to itself?

+
Yes, a fraction is always equivalent to itself since its value doesn’t change when both the numerator and the denominator are multiplied or divided by the same number.
How can I check if two fractions are equivalent?
+
You can check by cross-multiplying the numerators with the denominators of the other fraction. If the products are equal, the fractions are equivalent.