5 Easy Tricks to Solve Compound Shapes Areas

Calculating the areas of compound shapes might seem challenging, but with a few straightforward techniques, you can approach these problems with confidence. Whether you're dealing with an architectural blueprint, planning a garden layout, or solving complex geometric problems, understanding how to break down and solve these shapes is invaluable. In this blog post, we'll walk you through five easy-to-understand tricks that will not only help you calculate the area of compound shapes but also make the process enjoyable and educational.
Trick 1: Break It Down


The simplest way to tackle a compound shape is by breaking it into simpler, familiar shapes. Here's how:
- Identify Component Shapes: Look at the compound shape and find smaller, recognizable shapes like rectangles, triangles, or circles.
- Calculate Individual Areas: Work out the area of each component shape using well-known formulas.
- Sum or Subtract Areas: Depending on the arrangement, either add the areas together or subtract the areas of overlapping or unwanted parts.
🔹 Note: If a shape overlaps another, carefully subtract the overlapping area to get the correct final area.
Trick 2: Use the Addition-Subtraction Technique
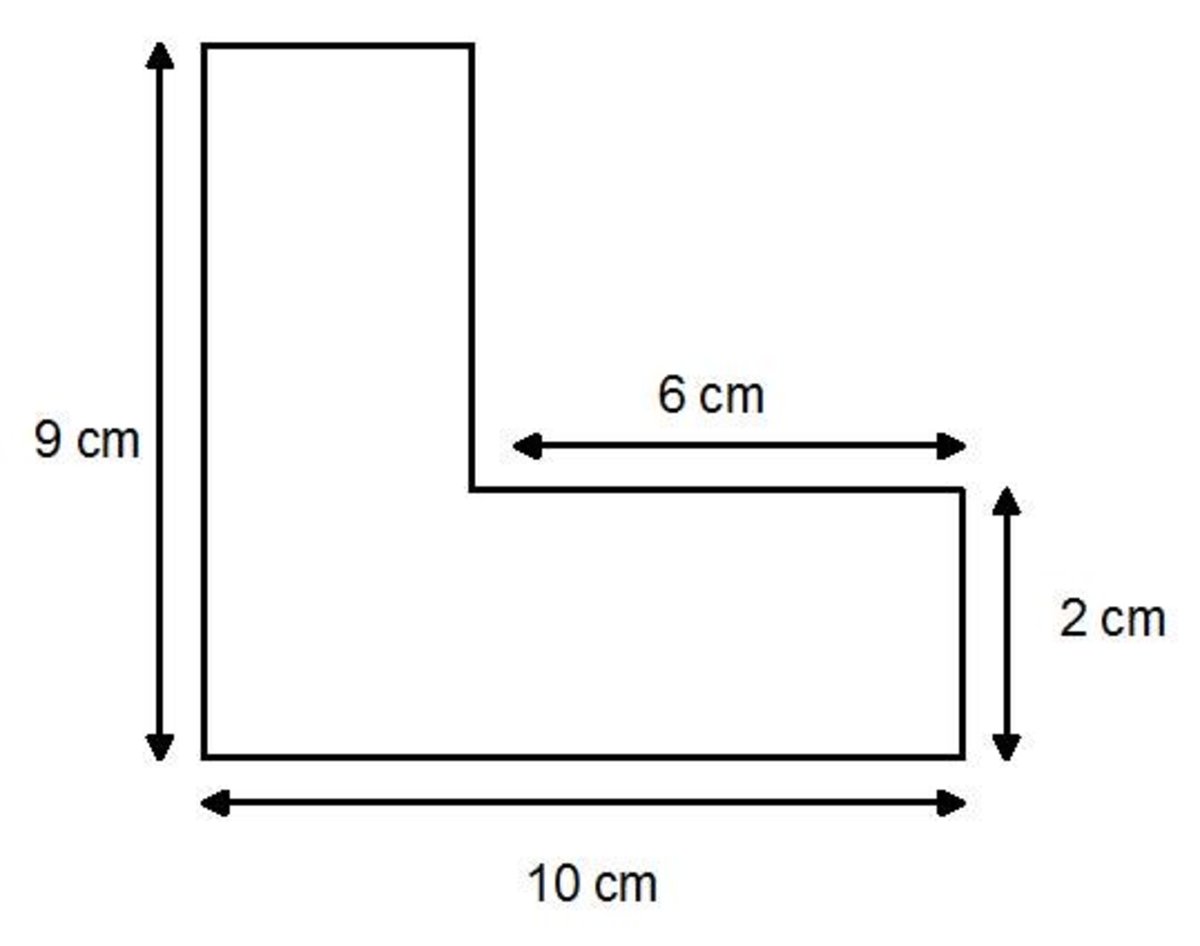

Sometimes, shapes are designed to be calculated in an additive or subtractive manner:
- Add Shapes Together: If the compound shape can be seen as a combination of simpler shapes that are entirely separate from one another, add their areas.
- Subtract Overlapping Areas: For shapes where parts of one shape overlap another, calculate the total area of the shape that includes the overlap and then subtract the area of the overlap.
🔹 Note: This method works well for shapes where one part is inscribed within another.
Trick 3: Visualization with Coordinate Geometry


Coordinate geometry can make calculations of area much easier:
- Plot the Shape: Use a coordinate plane to plot the vertices of the compound shape.
- Find Vertices: Determine the coordinates of key points that form the compound shape.
- Use the Formula: Apply the Shoelace Theorem or other coordinate geometry formulas to find the area directly.
| Vertex | X-coordinate | Y-coordinate |
|---|---|---|
| A | 2 | 3 |
| B | 5 | 7 |
| C | 10 | 6 |
| D | 6 | 2 |
| A | 2 | 3 |

🔹 Note: Coordinate geometry is especially useful when shapes are not in standard form or have irregular boundaries.
Trick 4: Employ Grids or Graph Paper


For visual thinkers, using a grid or graph paper can simplify the task:
- Draw the Shape: Sketch the compound shape onto grid paper at a suitable scale.
- Count Squares: Count the full and partial squares within the shape to estimate the area.
- Estimation: If necessary, estimate the partial squares or use fractions for a more precise calculation.
🔹 Note: This method is excellent for beginners and provides a quick way to verify calculations visually.
Trick 5: Application of the Trapezoid Rule


The trapezoid rule can simplify the area calculation of any polygon:
- Divide into Trapezoids: Break the compound shape into trapezoids (a four-sided polygon with one pair of parallel sides).
- Use the Formula: Apply the trapezoid area formula for each trapezoid and sum the areas.
Here's the formula for the area of a trapezoid:
\[ \text{Area} = \frac{1}{2} \times (base_1 + base_2) \times height \]🔹 Note: This trick can be more complex but is very effective for shapes with no right angles or when exact measurements are needed.
Through these five techniques, you've learned how to approach and solve the challenge of finding the areas of compound shapes. Each method brings its own advantages, depending on the shape's complexity, your comfort with geometry, and the tools available. Remember, the key to mastering compound shape area problems lies in breaking them down, understanding their components, and choosing the most fitting calculation technique. Practice these tricks regularly, and you'll find yourself solving even the most intricate shapes with ease and accuracy.
What if the compound shape has curved boundaries?

+
Curved shapes require specific formulas like the circular area formula. For more complex shapes, you might need to use calculus to find the area under curves.
Can these tricks be used for three-dimensional shapes?

+
Yes, but the process is more complex. You would need to consider volume and surface area calculations, often involving more advanced mathematical concepts like double integrals for irregular volumes.
How accurate are these methods?

+
The accuracy depends on the precision of your measurements and calculations. Grid and trapezoid methods offer visual estimation, which can be less precise but good enough for many practical purposes.