5 Ways to Easily Calculate Triangle Areas

Understanding how to calculate the area of different types of triangles can be very useful, whether you're working on geometry homework, engineering projects, or simply want to refresh your mathematical skills. In this post, we will explore five different methods to determine the area of triangles, each suited to different scenarios.
1. The Basic Area Formula
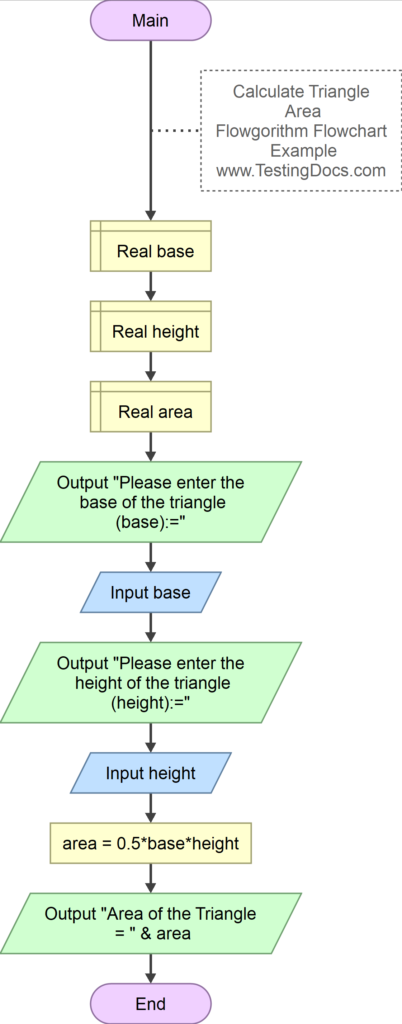
The most straightforward way to calculate the area of any triangle is by using the formula:
Area = 1⁄2 × base × height
- Base: Any side of the triangle can be considered the base.
- Height: The perpendicular height from the base to the opposite vertex.

📐 Note: Ensure that the height is drawn perpendicularly from the base to the opposite vertex; otherwise, the area calculation will be incorrect.
2. Heron’s Formula

When you don’t know the height but have all three sides of the triangle, you can use Heron’s formula:
Area = √[s(s - a)(s - b)(s - c)]
- s = (a + b + c)/2, where a, b, and c are the lengths of the triangle’s sides.

🔍 Note: Heron's formula is particularly useful when working with irregular or obtuse triangles where finding the height is not straightforward.
3. The Sine Rule for Area

If you know two sides and the angle between them:
Area = 1⁄2 × a × b × sin©
- a and b: Two sides of the triangle.
- C: The included angle between sides a and b.

🧮 Note: The sine rule allows for the calculation of area when the triangle's height is difficult to measure directly.
4. Using Coordinates

When the vertices of the triangle are given as points in a coordinate plane:
Area = | (Ax(By - Cy) + Bx(Cy - Ay) + Cx(Ay - By)) | / 2
- A, B, and C are the vertices of the triangle with coordinates (Ax, Ay), (Bx, By), and (Cx, Cy).
| Point | X Coordinate | Y Coordinate |
|---|---|---|
| A | Ax | Ay |
| B | Bx | By |
| C | Cx | Cy |

📍 Note: This method is convenient in computer graphics or when working with points on a Cartesian plane.
5. Using Trigonometry and Sides

Another trigonometric method for calculating the area when you know the sides and angles:
Area = (1⁄2)bc × sin(A) = (1⁄2)ac × sin(B) = (1⁄2)ab × sin©
- a, b, c: Sides of the triangle.
- A, B, C: Opposite angles to these sides.
In wrapping up, mastering these five methods provides you with versatile tools to tackle various triangle problems. Whether you’re using simple formulas like the base and height approach or delving into trigonometric or coordinate-based calculations, each method serves a unique purpose and situation. The variety ensures you can solve for areas regardless of how much information you have about the triangle.
Which method is best for calculating the area of a triangle?

+
The best method depends on the information you have. If you know the base and height, the basic formula is simplest. If you only have the sides, use Heron’s formula or coordinate method if the vertices are known in a plane.
Can I use these methods for all types of triangles?

+
Yes, each method can be applied to different types of triangles, from equilateral to scalene, as long as the required measurements are known.
Why are there so many methods to calculate triangle areas?
+
The variety in methods reflects different real-world applications and the mathematical flexibility required to solve problems with varying known variables.