Area Of A Triangle Worksheets
In the dynamic and ever-evolving world of mathematics, understanding the basic geometric shapes and their properties forms the cornerstone of advanced study. Among these, the concept of triangles is particularly significant. Triangles, with their three sides and three angles, are not just a basic shape; they are the fundamental building blocks of more complex structures in mathematics, architecture, engineering, and various other fields. Today, we delve into an essential aspect of triangles: calculating their area. This post will explore Area of a Triangle Worksheets, which are invaluable tools for learning, practice, and mastery in this topic.
Why Focus on the Area of a Triangle?

The importance of understanding the area of a triangle cannot be overstated. Here are a few reasons why this topic is so crucial:
- Foundation for Advanced Topics: Grasping how to find the area of a triangle sets the stage for understanding more advanced geometric and trigonometric concepts.
- Real-world Applications: From calculating land areas to designing objects and structures, the ability to compute the area of triangles has numerous practical applications.
- Developing Analytical Skills: Working with triangles helps in honing analytical and logical thinking, crucial for problem-solving in various disciplines.
The Formula for the Area of a Triangle

Before we dive into worksheets, let’s recap the basic formula for finding the area of a triangle:
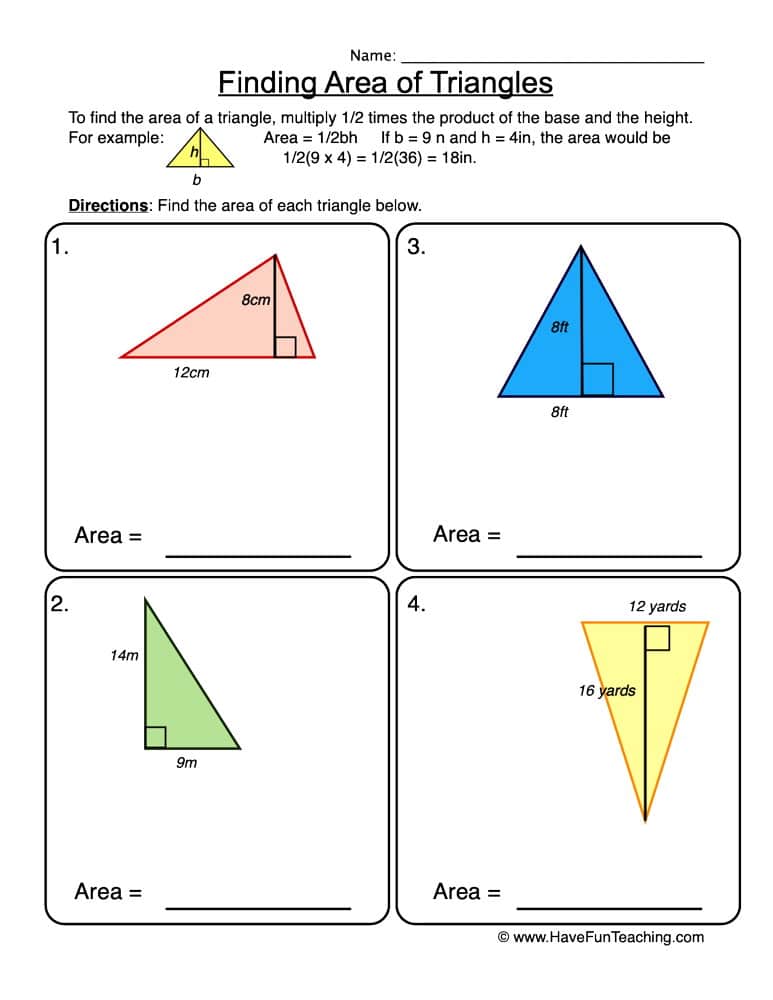
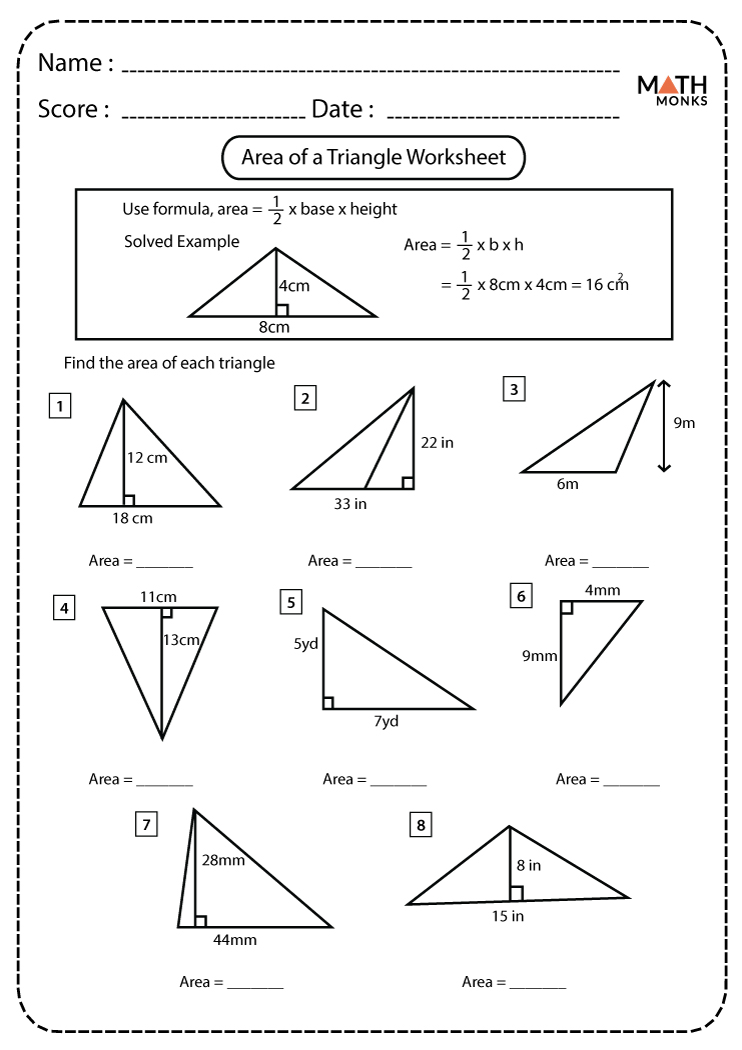
Area = (Base × Height) / 2
This formula is straightforward but versatile, accommodating triangles where the base and height are given or can be measured or calculated.
How to Utilize Area of a Triangle Worksheets

Worksheets are an effective learning tool, especially when it comes to geometric concepts. Here’s how you can make the most out of area of a triangle worksheets:
- Step-by-Step Problem Solving: Worksheets usually present problems in a sequence from simple to more complex, allowing for progressive learning.
- Repetition for Mastery: Repeated exposure to the formula and its applications through diverse problems helps solidify understanding.
- Visual Understanding: Many worksheets include diagrams or graphics, which can aid in visualizing how different triangles behave when their dimensions change.
Types of Area of a Triangle Worksheets

There are several types of worksheets available to cater to different learning stages and objectives:
1. Basic Worksheets
These are tailored for beginners:
- Triangles with given base and height.
- Calculating areas where only one triangle is involved.
2. Intermediate Worksheets
Aimed at learners with some background in geometry:
- Problems where height or base needs to be calculated or derived from given information.
- Introduction to special types of triangles like isosceles, equilateral, or right-angled triangles.
3. Advanced Worksheets
Designed for students delving deeper into geometry:
- Use of coordinate geometry to find areas.
- Word problems that require conceptual understanding and application of various triangle properties.
📚 Note: Some worksheets might also incorporate real-life scenarios, making the learning experience more relatable and engaging.
Designing Your Own Worksheets

If the available worksheets don’t meet your needs or if you wish to tailor learning to specific areas of focus, here’s how you can design your own:
- Set Objectives: Determine what aspects of triangles you want to explore (e.g., height calculation, area of composite shapes).
- Create Problem Sets: Draft problems that range from basic calculations to complex scenarios.
- Include Visuals: Use diagrams or illustrations to help students visualize the problem. This aids in understanding and solving.
- Test for Clarity: Ensure each problem is clear and solvable with the knowledge level expected from your audience.
Below is a simple table outlining the progression of difficulty in triangle area problems:
| Level | Description |
|---|---|
| Beginner | Straightforward problems with given dimensions, including basic algebraic substitution. |
| Intermediate | Involves trigonometry or coordinate geometry, special triangle properties, or multiple step problems. |
| Advanced | Real-world applications, use of Heron's formula or calculus, complex geometry problems. |

🔎 Note: When designing problems, consider students’ prior knowledge and learning pace to ensure an optimal challenge level.
The use of area of a triangle worksheets not only facilitates learning but also serves as a diagnostic tool for teachers and parents. By observing how students tackle these problems, educators can identify areas where further instruction might be needed or where students excel, tailoring their teaching strategies accordingly.
As we wrap up our discussion, we understand that the journey through geometric shapes, particularly triangles, is both fascinating and complex. The worksheets provide a structured approach to understanding the area of a triangle, which is a fundamental concept with wide-reaching applications. They act as stepping stones for learners at all levels, from beginners to advanced students, fostering an environment where mathematical concepts are not just learned but truly understood and applied.
What are the different formulas for calculating the area of a triangle?

+
The most common formula for the area of a triangle is (Base × Height) / 2. However, other formulas include:
- Heron’s Formula: (A = \sqrt{s(s-a)(s-b)(s-c)}), where (s) is the semi-perimeter and (a, b, c) are the sides.
- Using Trigonometry: (A = \frac{1}{2}ab \sin©), where (a) and (b) are sides, and (C) is the included angle.
- Using Coordinates: If vertices of the triangle are known, use the determinant formula for area.
Can the area of a triangle be found if only its three sides are given?
+
Yes, you can find the area of a triangle knowing only its sides by using Heron’s Formula. This formula requires the length of all three sides to calculate the area without knowing the height.
Why are worksheets effective in learning about triangles?

+
Worksheets offer a structured way to practice and understand geometric concepts:
- They provide visual aids which are crucial in geometry.
- Problems range from simple to complex, allowing for progressive learning.
- They encourage repetition, which helps solidify understanding.
- Teachers can use them to assess student progress and understanding.