5 Essential Tips for Mastering Fractions Easily
In the realm of mathematics, fractions can be a challenging topic for many students. However, with the right techniques and understanding, mastering fractions can become not just manageable but an enjoyable part of learning math. Here are five essential tips that can help you conquer fractions with ease and confidence.
Understand the Basics

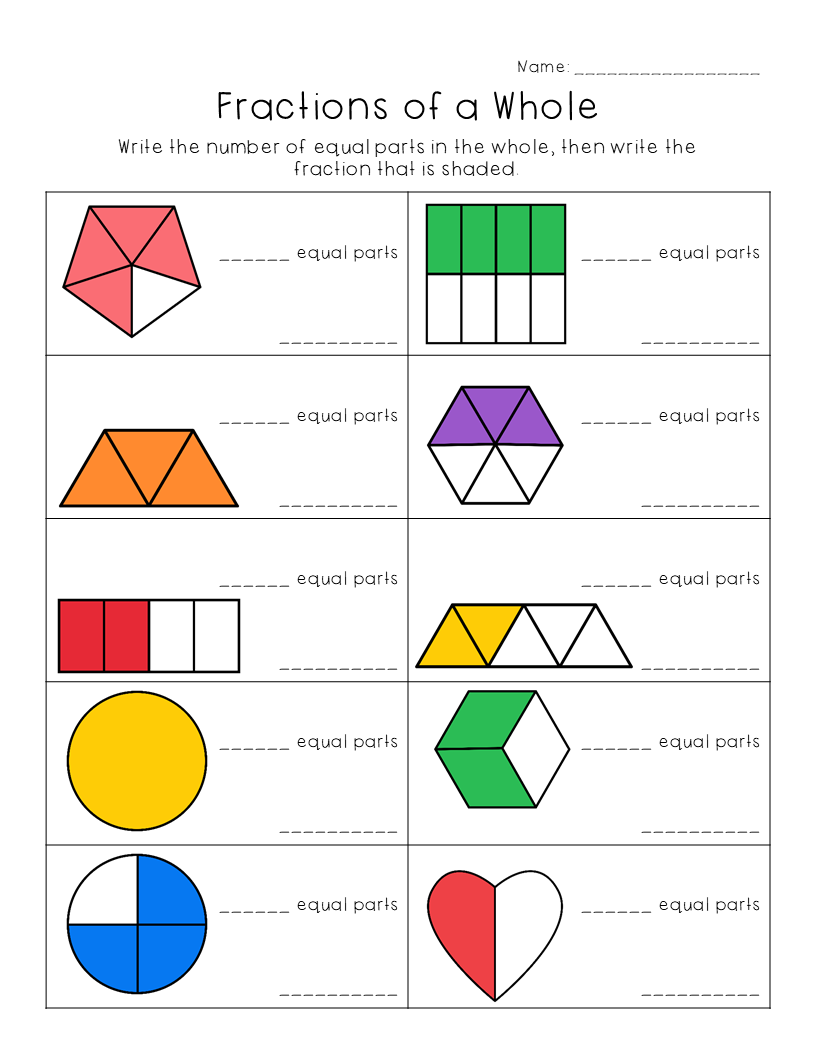
Before diving into complex fraction problems, it's crucial to solidify your understanding of what a fraction represents. A fraction consists of a numerator (the top number) and a denominator (the bottom number), which together describe a part-to-whole relationship.
- A fraction tells you how many parts of a whole you are considering.
- The denominator indicates how many equal parts the whole is divided into.
- The numerator shows how many of those parts you have.
By visualizing this concept, whether through diagrams or manipulatives like fraction circles or bars, you can gain a better intuitive grasp on fractions.
Simplify Whenever Possible

Fractions are often presented in a form that can be simplified to express the same value in fewer terms. Here are steps to simplify fractions:
- Identify the greatest common divisor (GCD) of both the numerator and the denominator.
- Divide both numbers by this GCD to obtain the simplest form.
Simplifying not only makes fractions easier to work with but also helps in comparing them more effectively:
💡 Note: Reducing a fraction to its simplest form does not change its value, only its appearance.
Add and Subtract with Like Denominators

| Operation | Process |
|---|---|
| Addition | Add the numerators and keep the denominator the same. |
| Subtraction | Subtract the numerators and keep the denominator the same. |

- Only perform these operations directly when the denominators are the same; otherwise, find the least common denominator (LCD).
- After the operation, remember to simplify if possible.
Multiply and Divide With Ease

Multiplying and dividing fractions is often seen as daunting, but with these steps, it becomes straightforward:
- To multiply, multiply the numerators together to form the new numerator, and do the same with the denominators to get the new denominator.
- Dividing by a fraction is the same as multiplying by its reciprocal (flipping the numerator and the denominator).
Again, simplify the result to make the final fraction as simple as possible.
Use Visual and Hands-On Learning
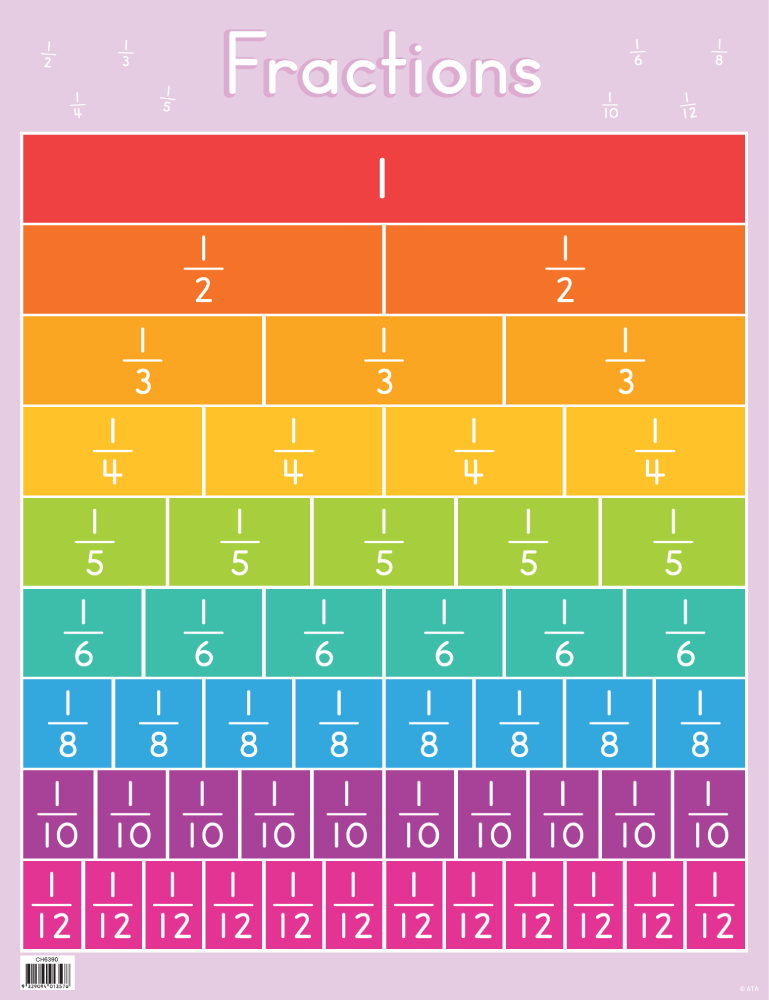
Incorporating visual aids and hands-on activities can enhance your understanding of fractions:
- Pizza or Pie Models: Use real or virtual slices of pizza or pie to represent parts of a whole.
- Fraction Bars: These can visually depict different fractions, making it easier to understand their relationships.
- Paper Folding: Fold paper to see how different denominators divide the whole.
Engaging with fractions physically or virtually provides a tactile approach that often helps in retention and understanding.
These five tips cover the foundational elements of fraction mastery, providing tools and techniques to make the process more intuitive and less intimidating. Remember, consistent practice with real-world applications can turn these tips into skills. Embrace the logic behind each step, and fractions will not only become a familiar part of your mathematical toolkit but also a subject you might find enjoyment in exploring further.
Why are fractions important in everyday life?

+
Fractions are crucial in cooking, measuring, budgeting, and understanding proportions in various contexts, making them indispensable in daily activities.
How can I practice fractions regularly?

+
Use fraction-based puzzles, cooking recipes, or even DIY projects to integrate fractions into your daily routine. Online resources like math games or problem sets can also provide structured practice.
What are some common mistakes when working with fractions?

+
Common mistakes include adding/subtracting numerators and denominators directly, not simplifying results, forgetting to change the operation when dividing fractions, or assuming unlike denominators can be combined as-is.