Arc Length Practice: Answers Included
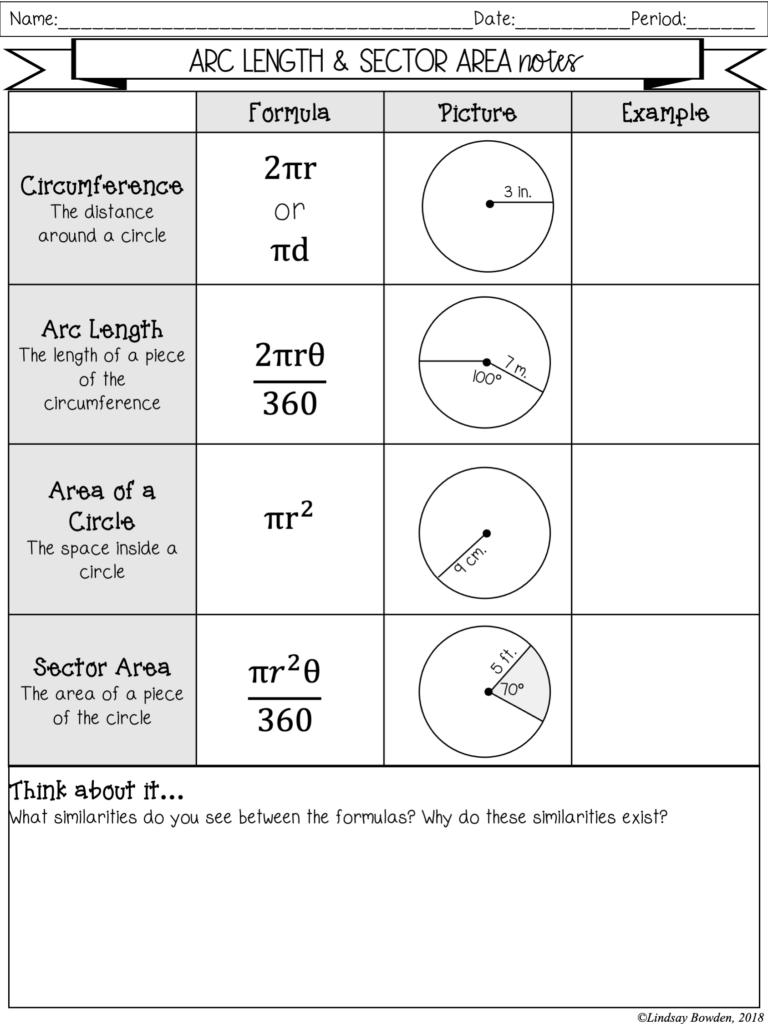
In the fascinating world of calculus, understanding how to calculate the arc length of a curve is not just about mastering mathematical concepts; it's about appreciating the beauty of mathematics in describing physical phenomena. The arc length of a curve is defined as the distance along the curve from one point to another, and today, we're diving deep into this topic, providing you with a practice guide along with comprehensive answers. Let's unfold the intricacies of calculating arc length with real-life examples and detailed explanations.
Understanding Arc Length

Calculating arc length can be intuitive when dealing with simple shapes like circles or straight lines. For instance, the arc length of a segment on a circle is given by:
| Formula | Description |
|---|---|
| L = rθ | Where L is the arc length, r is the radius, and θ is the angle in radians. |

However, for more complex curves, especially those defined by functions, the calculation becomes more intricate due to the need to account for the curve's bending or curvature.
The Arc Length Formula for Functions
Given a function y = f(x), the arc length from a to b on the x-axis can be calculated by:
Arc Length = ∫[sqrt(1 + (dy/dx)^2)] dx from a to b
Here's what each part signifies:
- 1: The constant term, representing the segment's length in the x-direction.
- (dy/dx)^2: The square of the derivative, accounting for the curve's slope.
- Integration: Summing up infinitesimally small segments along the curve.
Worked Example: Arc Length Calculation

Let's take the function y = x^2 and calculate its arc length from x = 0 to x = 1.
The derivative of y with respect to x is:
dy/dx = 2x
Now, we need to calculate:
Arc Length = ∫[sqrt(1 + (2x)^2)] dx from 0 to 1
Let's solve it step-by-step:
- Integrate: ∫[sqrt(1 + 4x^2)] dx
- Use a substitution:
- Let u = 1 + 4x^2
- du = 8x dx
- dx = du / (8x)
- Substitute back into the integral:
- ∫[sqrt(u) / (8x)] du
- The integral becomes (1/8) ∫[u^(-1/2) / x] du
- Using properties of integration:
- (1/8) (u^(1/2) / (1/2)) = (1/8) * 2 * sqrt(u) = (1/4) * sqrt(u)
- Evaluate from u = 1 (when x = 0) to u = 5 (when x = 1):
- (1/4) * (sqrt(5) - 1)
- The arc length of the curve from x = 0 to x = 1 for y = x^2 is approximately 1.478.
📝 Note: While the calculus might seem daunting, breaking it down into steps and using substitution simplifies the process. Don't forget, the more you practice, the more intuitive these calculations become.
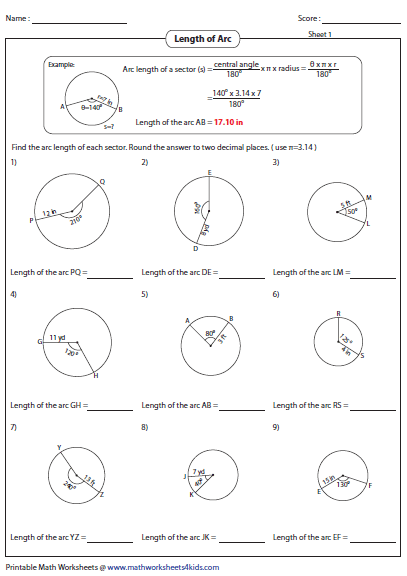
Practice Problems

Now, let's solidify your understanding with some practice problems. Here are a few examples with answers provided for self-assessment:
Problem 1

Find the arc length of y = 3x^3 from x = 1 to x = 2.
Problem 2

Calculate the arc length of the curve y = ln(sec x) from x = 0 to x = π/4.
Problem 3

Determine the arc length of y = 1 - x^2⁄4 from x = 0 to x = 4.
Arc Length for Parametric Curves

When dealing with parametric equations where x and y are functions of a parameter t, the arc length formula changes slightly:
Arc Length = ∫[sqrt((dx/dt)^2 + (dy/dt)^2)] dt
This approach allows us to handle curves that aren't easily expressible as functions of one variable.
Recapitulating the Journey

Our exploration of arc length has taken us through fundamental definitions, calculus-based formulas, real-life examples, and practice problems. By now, you should have a grasp on how to approach these calculations, understanding the interplay between the function's derivative and the curve's length. Remember, the journey through mathematics is one of constant learning and application, where each problem solved deepens your understanding and appreciation for the subject. Keep practicing, and let the beauty of calculus enlighten your path.
Why do we use arc length instead of straight-line distance?

+
Arc length measures the actual path along a curve, providing more accurate information about the distance traveled by an object following that path. This is particularly important in fields like physics and engineering where the curvature of the path matters.
What are some applications of arc length?
+
Applications include calculating the length of cables or ropes in suspension bridges, determining the length of threads in sewing, measuring distances in curvilinear paths in fields like robotics or surveying, and understanding the energy required to move along a curved trajectory in physics.
Can arc length be negative?

+
No, arc length represents a distance along a curve, and distance is inherently positive. However, if you’re moving in the negative direction along a curve, you would subtract that distance from the total path length if needed.