5 Must-Solve Pythagorean Theorem Word Problems With Answers

The Pythagorean Theorem is one of the most fundamental principles in geometry, providing a direct relationship between the sides of a right-angled triangle. Often represented as a2 + b2 = c2, where c is the hypotenuse and a and b are the other two sides, this theorem has numerous applications not just in theoretical mathematics but in everyday problem-solving as well. Here, we delve into five must-solve Pythagorean theorem word problems, complete with detailed answers, to illustrate its practical use.
1. Finding the Height of a Stepladder

Imagine you’re painting your bedroom ceiling, and you’re using an A-frame stepladder. If the ladder is 5 feet long when lying flat on the ground, and the distance from the base to where the ladder touches the ceiling is 4 feet, how high will the stepladder reach?
To solve this:
- Let a be the distance from the floor to the ceiling where the ladder touches, which is 4 feet.
- Let b be the height from the top of the ladder to the ceiling.
- Using the Pythagorean theorem, 52 = 42 + b2
- Solving this, b = √9 = 3 feet.
🏗️ Note: When measuring or using a ladder, always ensure safety by following the manufacturer’s guidelines for maximum extension and weight limits.
2. Measuring the Distance Across a Pond

Suppose you’re at one edge of a pond and wish to know the distance across to the other side without walking around. You can see a point directly opposite you on the other side, and you walk 40 meters away from this point. From your new position, you measure the distance to that point as 50 meters. How wide is the pond?
To solve:
- Let a be the distance you walked (40 meters).
- Let b be the width of the pond, which we need to find.
- The hypotenuse (distance from your new position to the opposite point) is 50 meters.
- 502 = 402 + b2
- Solving, b = √2500 - √1600 = 30 meters.
The pond’s width is 30 meters.
3. The Baseball Diamond Problem

A baseball diamond forms a perfect square with each side measuring 90 feet. If a player at third base hits the ball and runs to first base, how far does he run?
| Route | Legs | Calculation |
|---|---|---|
| Third to Home | 1 | 90 feet |
| Home to First | 1 | 90 feet |
| Straight Line | Diagonal | (90√2) feet |

The straight-line distance from third base to first base is the hypotenuse of the right triangle formed by the sides of the diamond, which is 90√2 ≈ 127.28 feet.
4. Roof Pitch Calculation

You need to replace the shingles on your roof, and you’ve measured the pitch of your roof to be a 4:12. This means for every 12 feet of horizontal run, the roof rises 4 feet. If you know the horizontal run is 30 feet, how long should each side of your roof be?
To find the length:
- Use the Pythagorean theorem where the base is 30 feet and the rise is (30⁄12) * 4 = 10 feet.
- The length of one side of the roof will be √(302 + 102) = √1000 ≈ 31.62 feet.
5. Firefighter’s Ladder Extension

A firefighter extends a ladder from the ground to a third-story window, forming a right angle with the ground. The base of the ladder is 15 feet from the building, and the ladder’s base is 15 feet from the window horizontally. If the window is 30 feet above the ground, how long must the ladder be?
To solve:
- Using the Pythagorean theorem where the base of the triangle is 15 feet and the height is 30 feet:
- Let c be the ladder’s length, then c2 = 152 + 302
- c = √1350 ≈ 36.74 feet.
These problems exemplify the Pythagorean theorem's utility in real-world applications, from construction to sports and even emergency services. Understanding and applying this theorem can simplify measurements, assessments, and planning in many fields. The versatility of the Pythagorean theorem proves its significance beyond the classroom, making it an essential tool for problem-solving in our daily lives.
What is the Pythagorean Theorem?
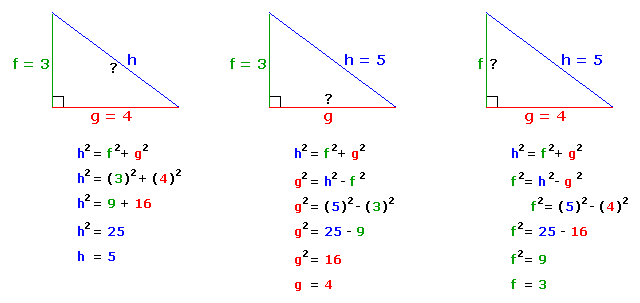
+
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. It is mathematically expressed as a2 + b2 = c2.
How does the Pythagorean theorem apply to real-life situations?

+
The Pythagorean theorem is used in various fields like architecture, engineering, navigation, and even in daily tasks like measuring distances or heights where direct measurement isn’t feasible. It helps in calculating distances, determining elevations, and in structural analysis.
Can the Pythagorean Theorem be used to check if a triangle is a right triangle?

+
Yes, if the square of one side (usually the longest side) of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle. However, this works only if all sides are measured correctly.