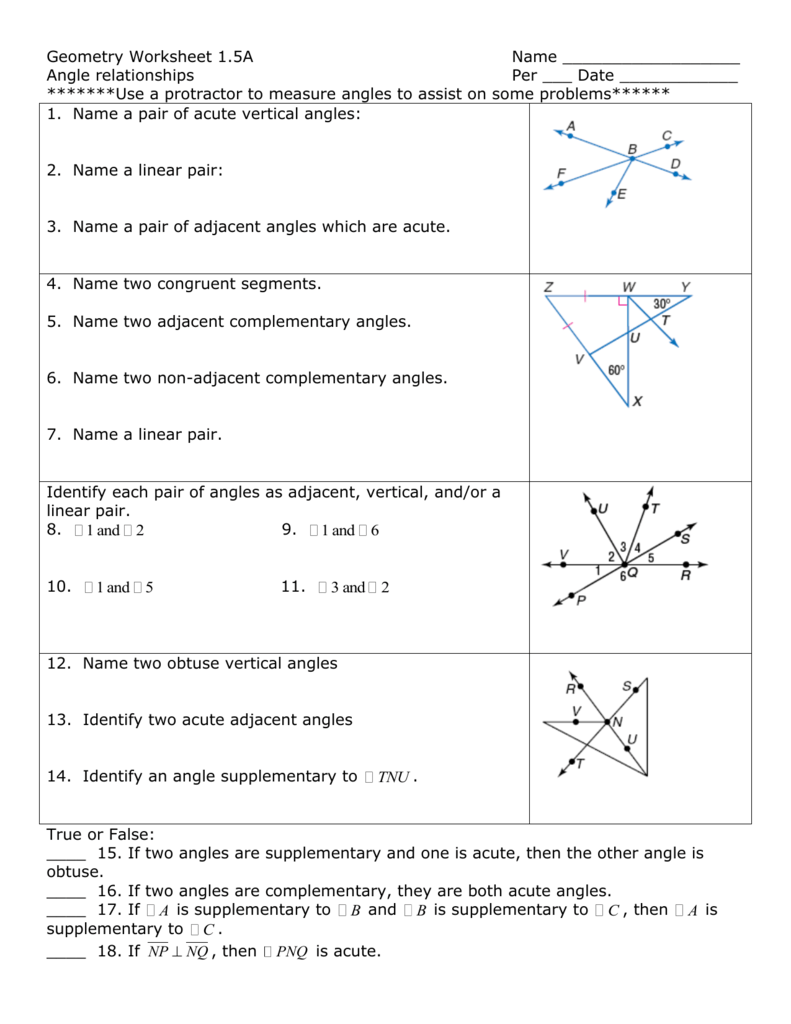
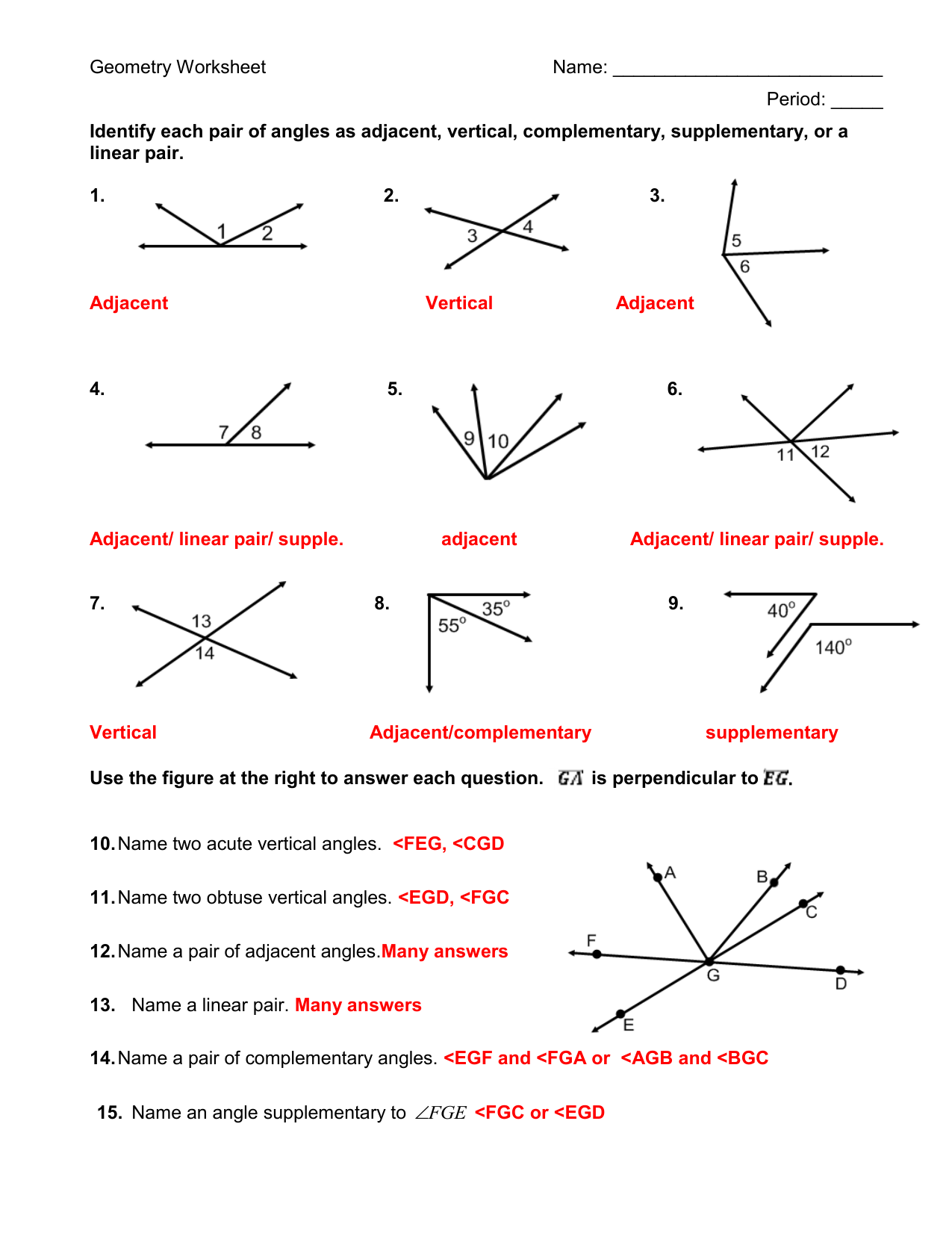
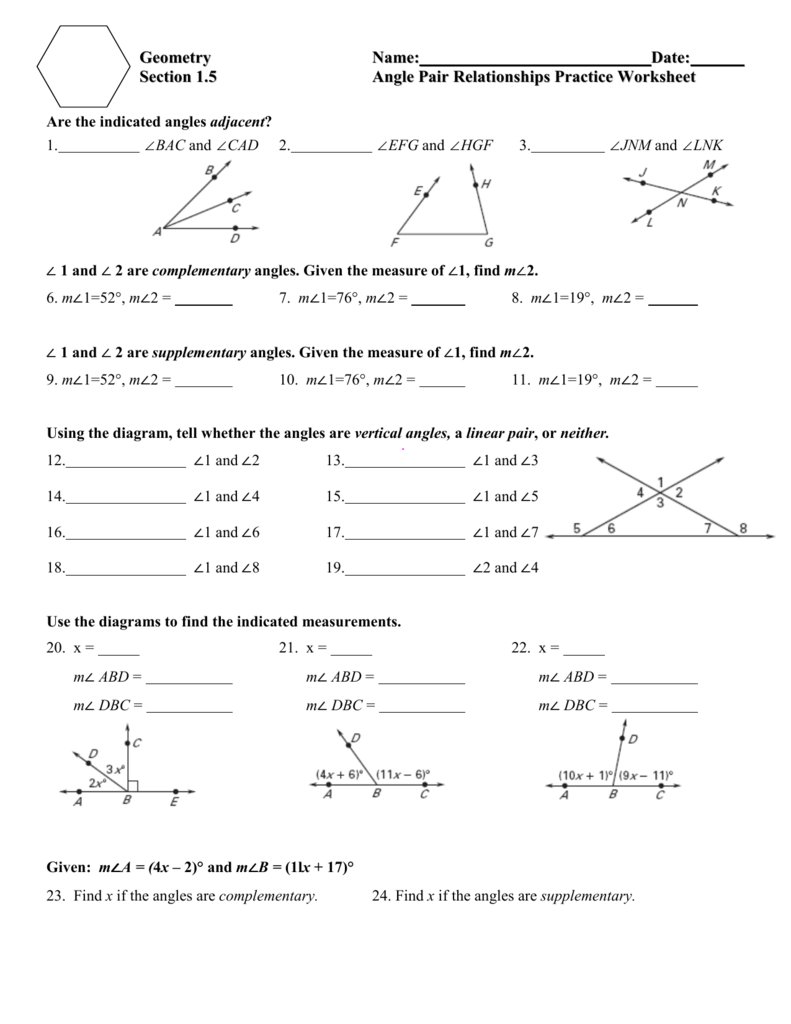
Angle Pairs Worksheet: Complete Answer Key Revealed

An angle pair worksheet is an invaluable tool for students and teachers alike, providing a structured practice in identifying and understanding the relationships between angles. These worksheets often cover various types of angle pairs, including complementary, supplementary, vertical, adjacent, and linear pairs. This comprehensive guide will walk you through an in-depth exploration of angle pairs, complete with explanations, examples, and a detailed answer key to help you master this essential topic in geometry.
Types of Angle Pairs

Understanding different types of angle pairs is fundamental in geometry. Here’s a breakdown:
- Complementary Angles: Two angles whose measures add up to 90 degrees.
- Supplementary Angles: Two angles whose measures add up to 180 degrees.
- Vertical Angles: These are opposite angles formed when two lines intersect. They are always equal in measure.
- Adjacent Angles: Two angles that have a common vertex and a common side but do not overlap. They can be complementary, supplementary, or form any other pair.
- Linear Pair: A pair of adjacent angles formed when two lines intersect, whose non-common sides form a straight line. The sum of these angles is always 180 degrees.
Worksheet Examples

Let’s look at some common problems found on angle pair worksheets:
Example 1: Complementary Angles

Given two angles, A and B, where A is 35 degrees. Determine the measure of angle B if they are complementary.
- Solution: Since A + B = 90 degrees, B = 90 - 35 = 55 degrees.
Example 2: Supplementary Angles

Angle C is 130 degrees. What is the measure of angle D if they form a supplementary pair?
- Solution: As C + D = 180 degrees, D = 180 - 130 = 50 degrees.
Example 3: Vertical Angles


Angle E is 70 degrees. What are the measures of angles F, G, and H?
- Solution: Vertical angles are equal, so:
- F = 70 degrees
- G = 110 degrees (as 180 - 70)
- H = 70 degrees (as it’s vertical to F)
Example 4: Adjacent Angles


Angle I is 40 degrees and angle J is 50 degrees. What type of pair do they form?
- Solution: Adjacent angles I and J are complementary (40 + 50 = 90 degrees).
Example 5: Linear Pair


Angle K is 65 degrees. What is the measure of angle L?
- Solution: Since K and L form a linear pair, L = 180 - 65 = 115 degrees.
🔍 Note: Always remember the basic principles of angle pairs. They provide the foundation for more complex geometric problems.
Answer Key for Common Worksheet Problems

Here is an answer key for some common problems on angle pair worksheets:
| Problem Type | Given Information | Solution |
|---|---|---|
| Complementary Angles | One angle is 35 degrees | The other angle is 55 degrees |
| Supplementary Angles | One angle is 130 degrees | The other angle is 50 degrees |
| Vertical Angles | Angle E = 70 degrees | Angles F, H = 70 degrees, Angle G = 110 degrees |
| Adjacent Angles | Angle I = 40 degrees, J = 50 degrees | The pair is complementary |
| Linear Pair | Angle K = 65 degrees | Angle L = 115 degrees |

In summary, mastering angle pairs is essential for understanding geometry. By recognizing the different types of angle pairs and how to solve problems related to them, students can develop a deeper appreciation for spatial relationships and the logic behind geometric proofs. Remember to practice these problems regularly to reinforce your understanding and ensure that the concepts become second nature.
What are the main types of angle pairs?

+
The main types of angle pairs include complementary, supplementary, vertical, adjacent, and linear pairs.
How do I identify a linear pair?

+
A linear pair consists of two adjacent angles whose non-common sides form a straight line, and their sum is 180 degrees.
Can two angles be both complementary and adjacent?
+
Yes, if two angles sum up to 90 degrees and they share a common vertex and side, they are both complementary and adjacent.
Why are vertical angles always equal?
+
Vertical angles are formed by the intersection of two lines. They are opposite and thus always equal due to the geometry of the intersection.