5 Steps to Master Slope-Intercept Equations Easily

Understanding the slope-intercept form of a line equation is pivotal for anyone delving into algebra, as it provides a straightforward way to analyze and graph linear equations. Whether you're a student, an educator, or just a curious learner, mastering this concept can significantly boost your mathematical capabilities. Here are five steps to help you become proficient with slope-intercept equations with ease:
Step 1: Understanding Slope-Intercept Form

The first step is to familiarize yourself with the basic form of the equation. The slope-intercept form of a line is written as:
y = mx + b
- m represents the slope of the line, which indicates how steep the line is.
- b denotes the y-intercept, where the line crosses the y-axis.
It’s crucial to understand that the slope shows how the y-value changes for every unit increase in x, and the y-intercept is where the line meets the y-axis when x equals zero.

Step 2: Calculating Slope

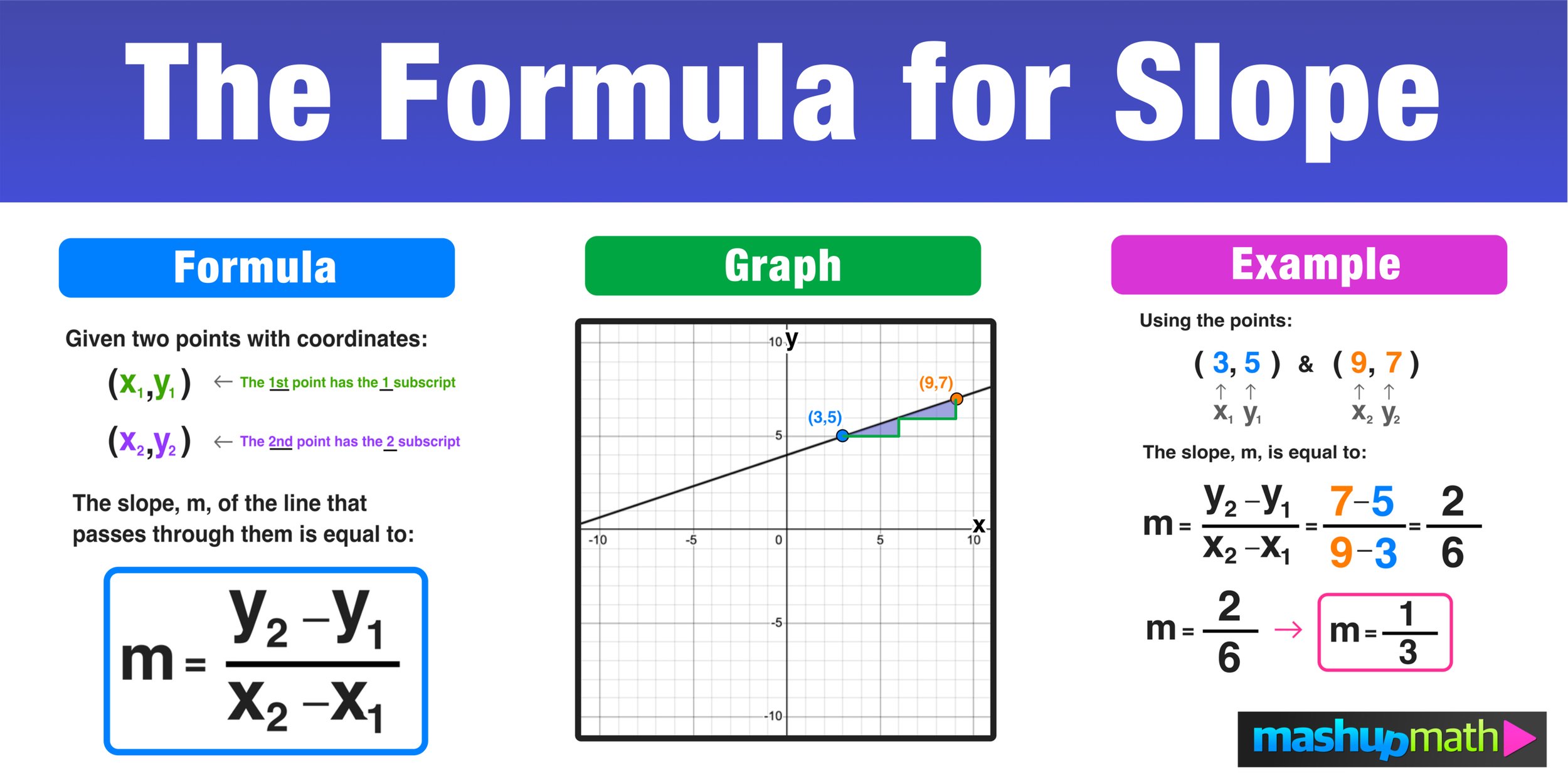
Knowing how to find the slope is essential:
- Given two points (x1, y1) and (x2, y2), the slope can be calculated using the formula:
m = (y2 - y1) / (x2 - x1)
📏 Note: Ensure that the order of subtraction is consistent when calculating slope.
Step 3: Determining the Y-Intercept
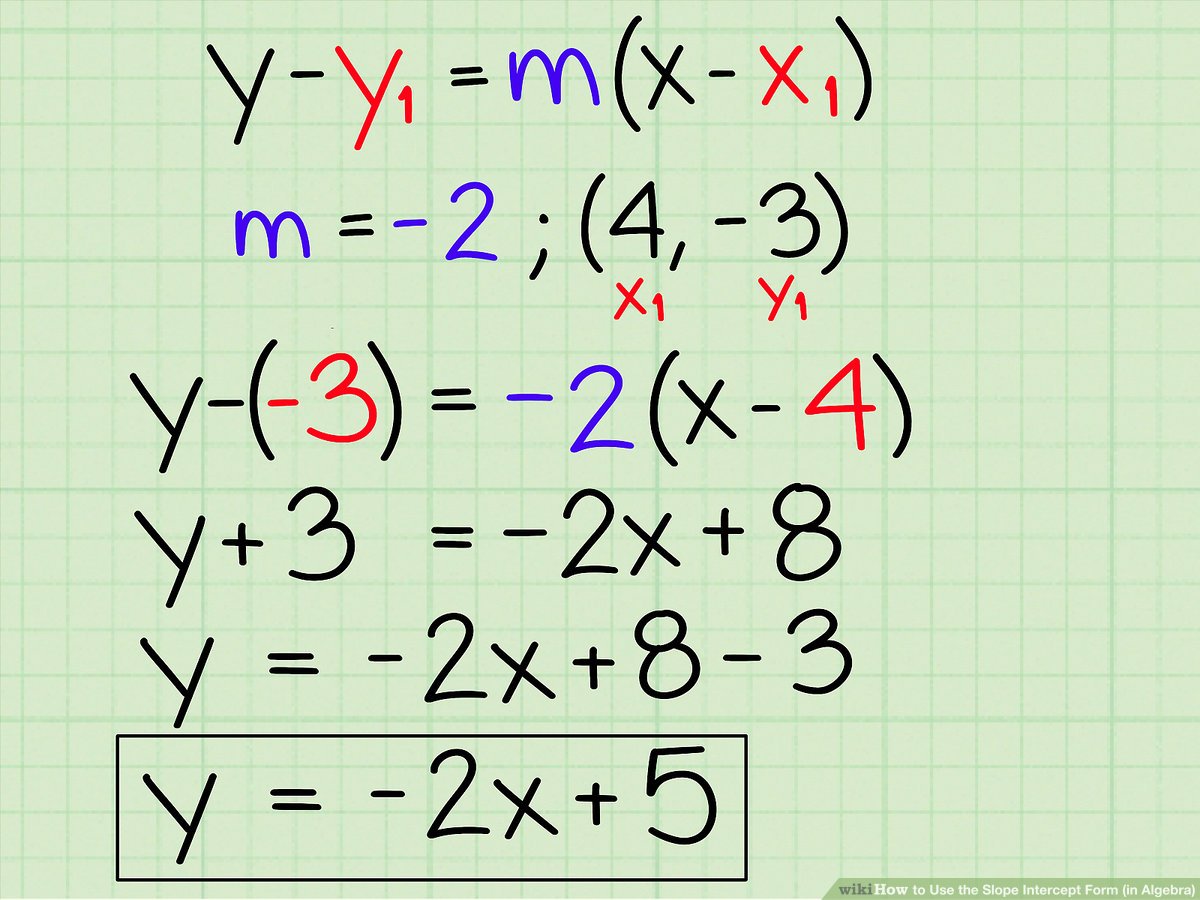
To determine the y-intercept (b), you can:
- Use the formula b = y - mx where x and y are from a point on the line.
- Read the y-intercept from the graph where the line crosses the y-axis.
🌐 Note: If a line equation is not in slope-intercept form, convert it to that form to find the y-intercept easily.
Step 4: Graphing Linear Equations
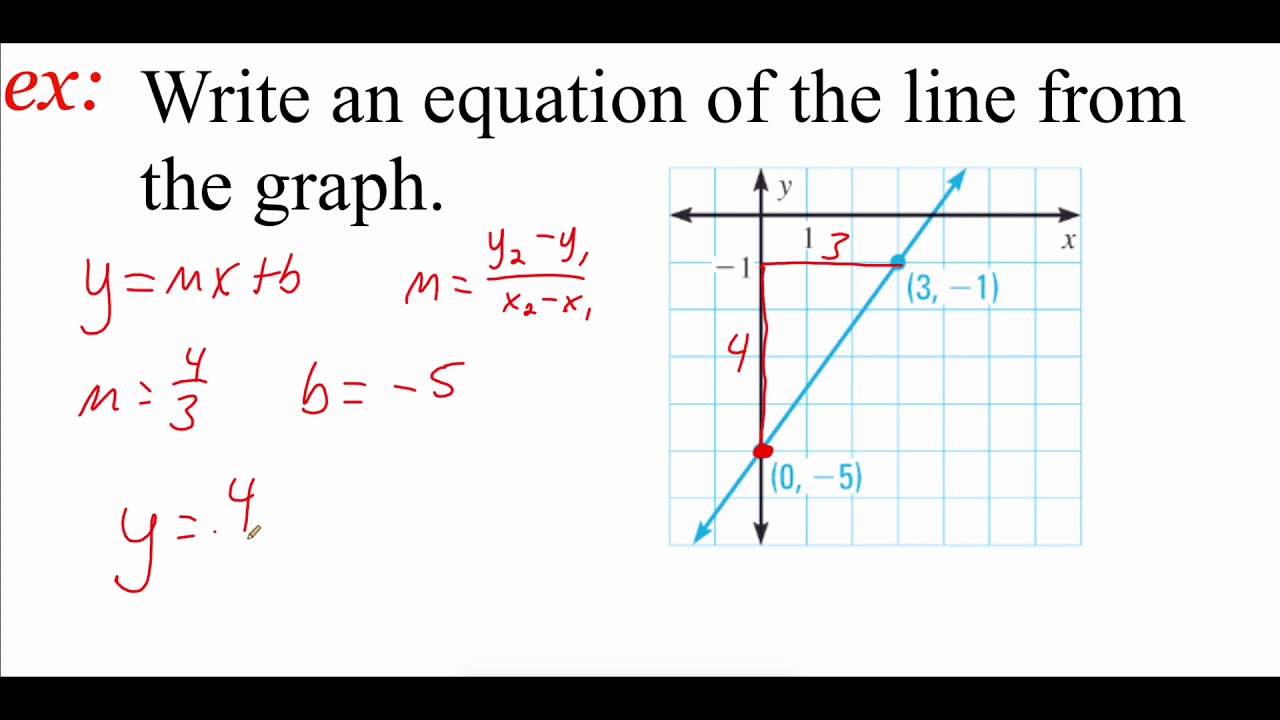
Now that you understand slope and y-intercept:
- Plot the y-intercept on the y-axis.
- Use the slope to plot additional points or to find another coordinate by stepping from the y-intercept.
- Connect these points to draw the line.
A practical example might help here:
| Step | Description |
|---|---|
| 1. Y-Intercept | Plot (0, b) on the graph. |
| 2. Slope | From the y-intercept, move rise over run. For m = 3⁄2, move 3 units up and 2 units to the right. |
| 3. Draw Line | Connect the dots you’ve plotted to form the line. |
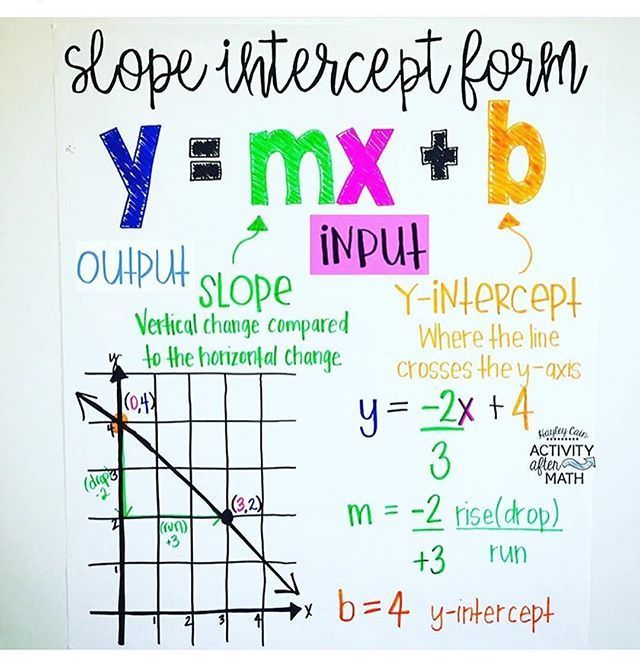
Step 5: Practice and Application

Consistent practice is key to mastering slope-intercept equations:
- Practice transforming equations into slope-intercept form.
- Work on real-world problems involving linear equations to solidify your understanding.
- Use graphing calculators or online tools to check your work.
🔧 Note: Real-world applications often require an understanding of linear relationships, so keep practicing in context!
By following these steps, you've embarked on a journey to master the fundamentals of slope-intercept equations. This knowledge will not only help you with graphing but also in various other mathematical and real-world scenarios. Keep practicing, and soon you'll see that equations are not just numbers and lines, but tools to understand patterns in data, optimize processes, and solve problems in daily life.
What does the slope represent in real-world scenarios?
+
In real-world scenarios, the slope often represents the rate of change. For example, if you’re plotting distance vs. time for a car, the slope would represent the car’s speed (distance per unit time).
How can I remember the slope-intercept formula?

+
Try using the mnemonic “slope is steep, y-intercept’s deep” where “steep” reminds you of ’m’ (slope) and “deep” of ‘b’ (y-intercept). Also, practicing the formula regularly will help in memorizing it.
Can I graph a line with just the slope and no y-intercept?

+
Yes, you can still graph a line using just the slope by choosing any point on the line and using the slope to find additional points. However, it’s much easier if you have the y-intercept or another point on the line.



