Inequalities Worksheet: Write and Graph with Ease
In the world of mathematics, inequalities present a unique challenge for students and educators alike. They require not just an understanding of basic algebraic concepts but also a visual interpretation that aids in comprehension. The process of writing and graphing inequalities is crucial in bridging the gap between the theoretical and the practical aspects of math. This article will guide you through the ins and outs of crafting and graphing inequalities with ease, ensuring that both students and teachers find the process accessible and rewarding.
Understanding Inequalities

Before diving into the specifics of writing and graphing, let’s understand what inequalities are. An inequality is a statement that expresses that two quantities or expressions are not equal. Here are the fundamental types:
- Less Than () - Signifies that the value on the left is smaller than the value on the right.
- Greater Than (>)** - Indicates that the value on the left is larger than the value on the right.
- Less Than or Equal To (≤) - Suggests that the left value is either less than or equal to the right value.
- Greater Than or Equal To (≥) - Implies that the left value is either greater than or equal to the right value.
- Not Equal To (≠) - Shows that the two expressions are not equal.
Writing Inequalities

To write inequalities effectively, you need to follow these steps:
- Identify the Variables: Determine which quantities or expressions are being compared.
- Choose the Correct Symbol: Based on the comparison, select the appropriate inequality symbol.
- Structure the Inequality: Place the variables and constants in a logical format, ensuring the inequality reads naturally.
💡 Note: When writing inequalities, always ensure that the variable (if any) is on the left side for consistency unless there is a specific reason to do otherwise.
Graphing Inequalities

Graphing inequalities gives a visual representation, making abstract concepts more concrete. Here’s how to graph them:
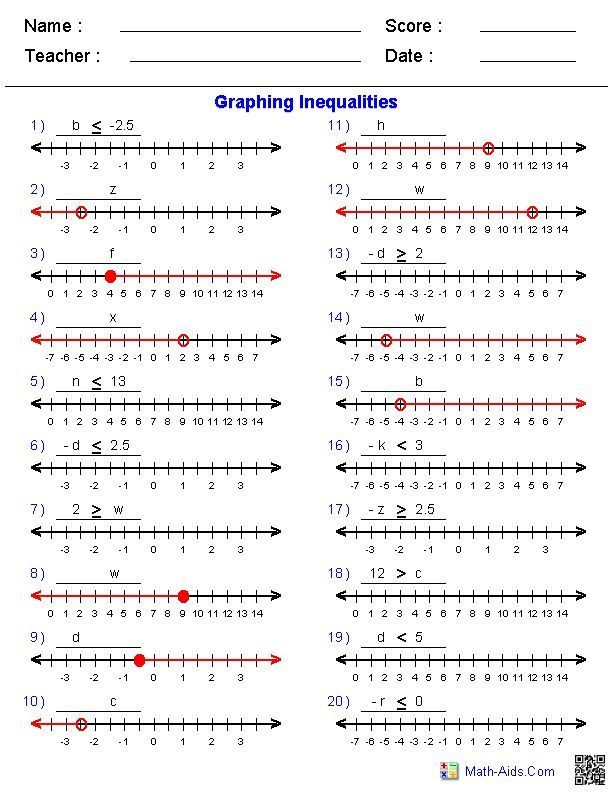
One-Variable Inequalities
For one-variable inequalities:
- Set Up the Number Line: Draw a number line, ensuring it has sufficient range.
- Identify the Solution Set: Determine the interval on the number line where the inequality holds true.
- Plot the Points: Use open circles for ‘less than’ or ‘greater than’ to indicate that the endpoint is not included, and closed circles for ‘less than or equal to’ or ‘greater than or equal to’ to show that the endpoint is included.
- Draw the Line: Extend the line from the endpoint in the direction of the solution.
Two-Variable Inequalities
Two-variable inequalities involve graphing in a coordinate plane:
- Draw the Boundary Line: First, replace the inequality with an equality to find the boundary line, which divides the plane into two parts.
- Test a Point: Choose a point not on the line to determine which side of the boundary line contains solutions to the inequality.
- Shade the Region: Shade the area containing all the solutions.
- Include Boundary Lines: Use solid lines if the inequality includes ‘or equal to’ (≤ or ≥), and dashed lines for strict inequalities (< or >).
Examples for Clarity

Let’s illustrate with examples:
One-Variable Inequality Example
Consider the inequality x ≤ 3:
- On the number line, place a closed circle at 3.
- Draw a line extending to the left, representing all numbers less than or equal to 3.
Two-Variable Inequality Example
Consider the inequality y > 2x + 1:
- Draw the line y = 2x + 1 (dashed since it’s a ‘greater than’ inequality).
- Test a point, say (0, 0), which does not satisfy the inequality.
- Shade the region above the line as this is where y is greater than 2x + 1.
⚠️ Note: Always double-check your boundary lines and shading to ensure accuracy in your graphs.
In education, the process of writing and graphing inequalities is pivotal in developing critical thinking and problem-solving skills among students. Understanding how to effectively communicate and visualize mathematical relationships through inequalities is a cornerstone of advanced mathematics. By practicing these steps, students not only grasp the algebraic concepts but also foster a deeper comprehension of how numbers and variables interact in different contexts.
This journey through writing and graphing inequalities provides a structured approach to mastering this mathematical topic. Remember, the key to success is consistent practice and ensuring that your approach aligns with the logical flow of the problem. Each step, from identifying variables to shading regions on the graph, contributes to a more intuitive understanding of inequalities.
Why do we use open and closed circles when graphing inequalities on a number line?

+
Open circles are used for strict inequalities (‘less than’ or ‘greater than’) to show that the endpoint is not part of the solution set. Closed circles are used for ‘or equal to’ inequalities to indicate that the endpoint is included in the solutions.
How can you test whether a region in the coordinate plane satisfies a two-variable inequality?

+
Choose a point not on the boundary line and substitute its coordinates into the inequality. If the statement is true, shade the side of the line that contains this point. If false, shade the opposite side.
What’s the importance of using the correct symbols in inequalities?

+
Using the correct inequality symbols ensures the accuracy of the mathematical statement. This precision is crucial in fields like engineering, finance, and science where incorrect calculations can have significant consequences.
Can inequalities have multiple solution sets?

+
Yes, complex inequalities or compound inequalities can result in multiple solution sets or regions where the statement holds true, often requiring the combination of several graphs or sets.
What are the educational benefits of teaching and learning inequalities?

+
Teaching inequalities helps students develop critical thinking skills, logical reasoning, and a better understanding of number relationships. It’s foundational for advanced mathematical topics, real-world applications in finance, and problem-solving in engineering and physics.