4 Ways to Solve Isosceles Triangle Problems Fast

Isosceles triangles are fascinating geometric figures due to their symmetry and unique properties. They come with two equal sides, and this single characteristic simplifies many problems related to angles, side lengths, and areas. Here's how to quickly master solving problems associated with isosceles triangles.
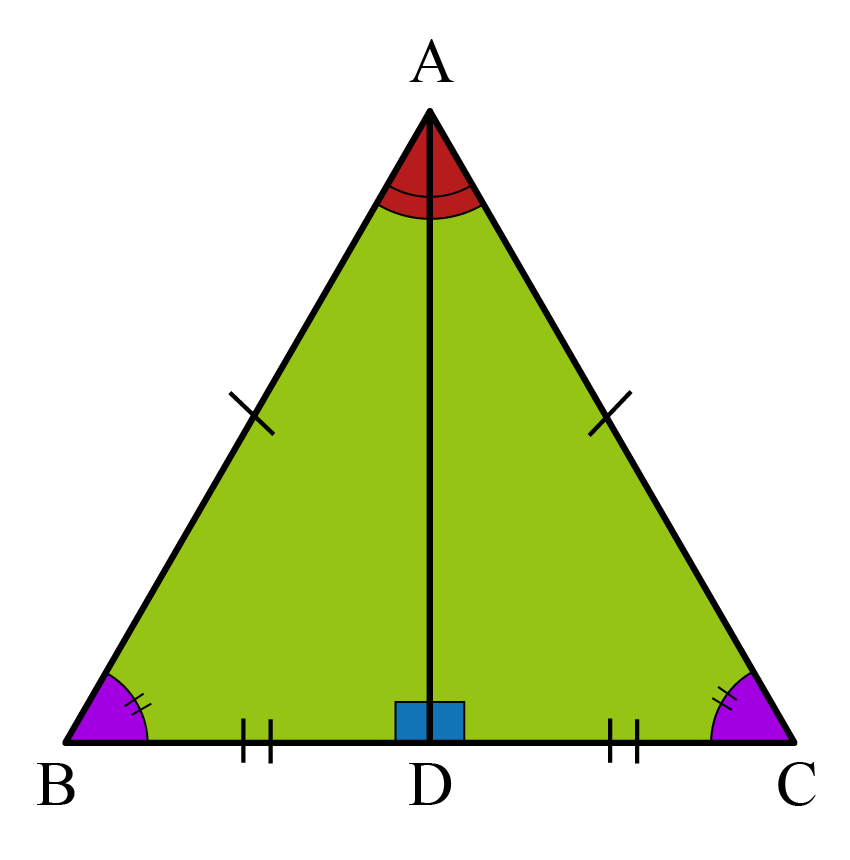
1. Recognizing the Unique Properties

The first step in solving problems involving isosceles triangles is to recognize their inherent symmetry. Key points include:
- The two equal sides are known as the legs of the triangle.
- Opposite these legs are equal angles known as base angles.
- The third side, often called the base, can be of any length different from the legs.

2. Using Symmetry for Angle Calculations

When you need to find unknown angles, here’s what you can do:
- If you know one base angle, the other will be the same because of symmetry.
- Sum of angles in any triangle is always 180 degrees. This allows you to calculate the vertex angle, or the angle opposite the base, by subtracting twice the base angle from 180 degrees.
For example, if one base angle is 45 degrees:
- Vertex angle = 180° - 2 * 45° = 90°
- Both base angles will be 45°
3. Applying Pythagorean Theorem for Side Lengths

When you’re looking to find the side lengths, use the Pythagorean theorem for isosceles triangles:
- If you have two legs of length (a) and a base (b), you can find the altitude (h) by:
- (h = \sqrt{a^2 - \left(\frac{b}{2}\right)^2})
Here is a simple table to illustrate:
| Leg (a) | Base (b) | Altitude (h) |
|---|---|---|
| 5 | 6 | ( \sqrt{25 - 3^2} \approx 4 ) |
| 10 | 8 | ( \sqrt{100 - 4^2} \approx 9.798 ) |
📌 Note: Pythagorean theorem works only if the triangle is right or can be divided into two right triangles.
4. Calculating the Area Efficiently

The area of an isosceles triangle can be found using two methods:
- Using base and height: Area = 0.5 * Base * Height
- Using Heron’s formula: If you only have side lengths, Heron’s formula can be employed. First, find the semiperimeter (s = \frac{a + a + b}{2} ), then calculate the area using ( \sqrt{s \times (s - a) \times (s - a) \times (s - b)} ).
Final Thoughts

Isosceles triangles, with their symmetrical nature, simplify geometric calculations significantly. Once you understand their properties and use the strategies outlined above, tackling isosceles triangle problems becomes more intuitive and less time-consuming. Remember, symmetry and the Pythagorean theorem are your keys to unlocking quick solutions in geometry involving isosceles triangles.
What if I don’t know any angles in an isosceles triangle?

+
If you know the side lengths, you can still solve for the angles using the law of cosines or by applying the Pythagorean theorem to find the altitude and then using the properties of the triangle.
Can you solve problems if only the base is known?

+
If the base is known, but not the legs, you would need additional information like the area or the fact that it’s a right triangle to proceed. Otherwise, you’re limited in what you can solve for without more data.
Are all isosceles triangles right triangles?

+
No, only some isosceles triangles are right triangles. An isosceles right triangle has two equal sides (legs) and one right angle at the vertex opposite the base.