Triangle Sum and Exterior Angle Theorem Explained
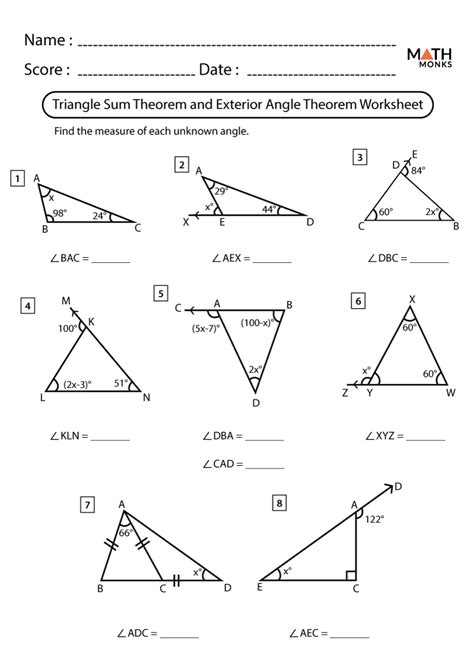
Understanding the Triangle Sum and Exterior Angle Theorem
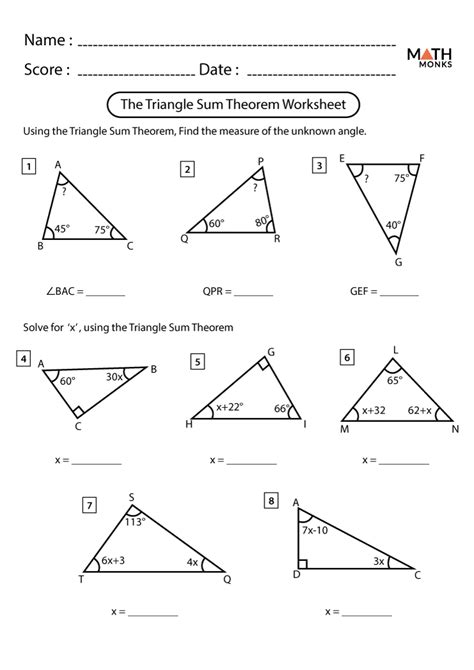
The triangle sum theorem and the exterior angle theorem are two fundamental concepts in geometry that help us understand the properties of triangles. In this article, we will delve into the world of triangles and explore these two theorems in detail.
What is the Triangle Sum Theorem?
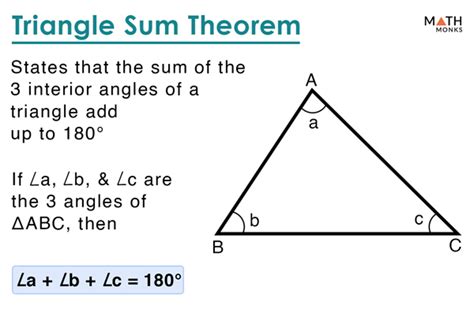
The triangle sum theorem states that the sum of the interior angles of a triangle is always 180 degrees. This theorem is also known as the angle sum property of triangles. The theorem can be mathematically represented as:
∠A + ∠B + ∠C = 180°
where ∠A, ∠B, and ∠C are the interior angles of the triangle.
📝 Note: The triangle sum theorem is valid for all types of triangles, including acute, right, obtuse, and equilateral triangles.
Proof of the Triangle Sum Theorem
There are several ways to prove the triangle sum theorem. One of the most common methods is to use the concept of parallel lines and transversals.
Imagine a triangle ABC, and draw a line parallel to side BC through point A. This line will intersect the extended side AB at point D.
Since line AD is parallel to line BC, the corresponding angles are equal. Therefore, ∠BAD = ∠BCA.
Similarly, ∠CAD = ∠BAC.
Now, consider the sum of the interior angles of triangle ABC:
∠A + ∠B + ∠C = ∠BAD + ∠CAD + ∠BCA
Substituting the equal angles, we get:
∠A + ∠B + ∠C = ∠BAD + ∠BAD + ∠BCA
Since ∠BAD and ∠BCA are supplementary angles, their sum is equal to 180°.
∠A + ∠B + ∠C = 180°
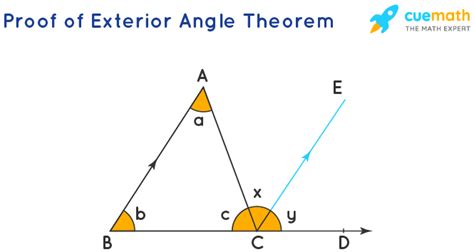
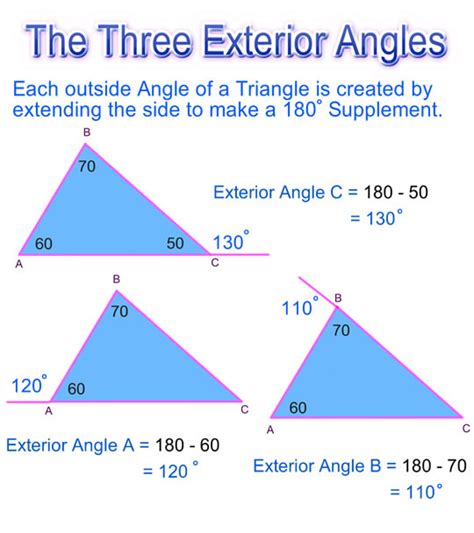
What is the Exterior Angle Theorem?
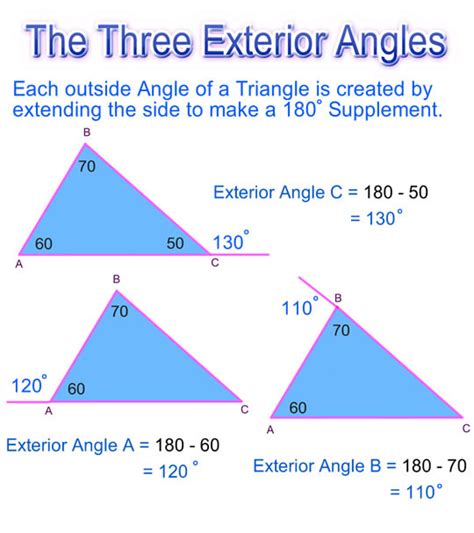
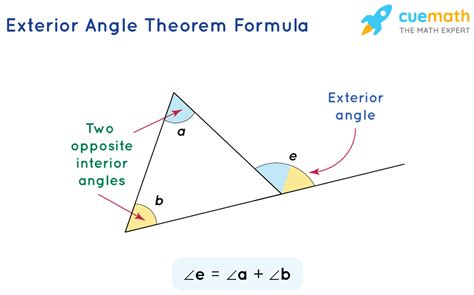
The exterior angle theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles.
Mathematically, the theorem can be represented as:
∠E = ∠A + ∠B
where ∠E is the exterior angle, and ∠A and ∠B are the remote interior angles.
📝 Note: The exterior angle theorem is valid for all types of triangles, including acute, right, obtuse, and equilateral triangles.
Proof of the Exterior Angle Theorem
The proof of the exterior angle theorem is similar to the proof of the triangle sum theorem.
Imagine a triangle ABC, and draw an exterior angle ∠E at vertex A.
Since line BC is a straight line, the sum of the interior angles ∠B and ∠C is equal to 180°.
∠B + ∠C = 180°
Now, consider the exterior angle ∠E. Since it is an exterior angle, it is supplementary to the interior angle ∠A.
∠E + ∠A = 180°
Substituting the sum of the interior angles ∠B and ∠C, we get:
∠E + ∠A = ∠B + ∠C
Since ∠A is a common angle, we can subtract it from both sides:
∠E = ∠B + ∠C
Relationship Between the Triangle Sum and Exterior Angle Theorems

The triangle sum theorem and the exterior angle theorem are closely related. In fact, the exterior angle theorem can be derived from the triangle sum theorem.
Consider a triangle ABC, and draw an exterior angle ∠E at vertex A.
Since the sum of the interior angles of the triangle is 180° (triangle sum theorem), we can write:
∠A + ∠B + ∠C = 180°
Now, consider the exterior angle ∠E. Since it is supplementary to the interior angle ∠A, we can write:
∠E + ∠A = 180°
Substituting the sum of the interior angles ∠B and ∠C, we get:
∠E + ∠A = ∠B + ∠C
Subtracting ∠A from both sides, we get:
∠E = ∠B + ∠C
This is the exterior angle theorem.
Real-World Applications of the Triangle Sum and Exterior Angle Theorems

The triangle sum and exterior angle theorems have numerous real-world applications in fields such as:
- Architecture: The theorems are used to design buildings and bridges.
- Engineering: The theorems are used to calculate stresses and loads on structures.
- Physics: The theorems are used to describe the motion of objects in three-dimensional space.
| Theorem | Real-World Application |
|---|---|
| Triangle Sum Theorem | Designing bridges and buildings |
| Exterior Angle Theorem | Calculating stresses and loads on structures |
Conclusion
In conclusion, the triangle sum theorem and the exterior angle theorem are two fundamental concepts in geometry that help us understand the properties of triangles. The theorems have numerous real-world applications in fields such as architecture, engineering, and physics. By understanding these theorems, we can solve problems and make calculations with ease.
What is the triangle sum theorem?
+
The triangle sum theorem states that the sum of the interior angles of a triangle is always 180 degrees.
What is the exterior angle theorem?
+
The exterior angle theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles.
What are some real-world applications of the triangle sum and exterior angle theorems?

+
The theorems have numerous real-world applications in fields such as architecture, engineering, and physics.
Related Terms:
- Triangle Sum Theorem Worksheet PDF



