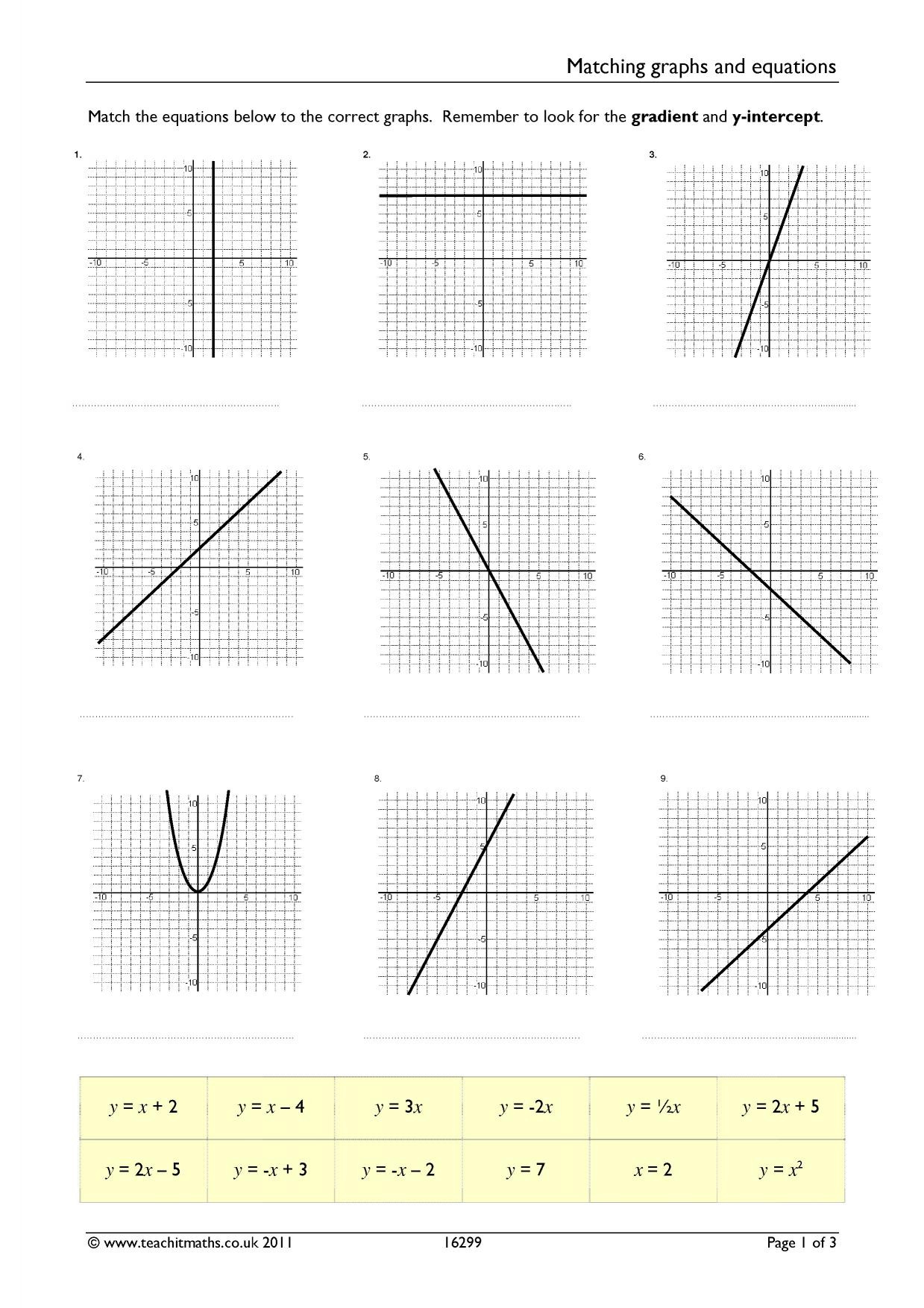
Graphing Linear Equations: Ultimate Worksheet with Answer Key

Welcome to our comprehensive guide on graphing linear equations! Whether you're a student grappling with algebra, a teacher looking for resources, or simply someone curious about the magic behind linear graphs, this worksheet will serve as an invaluable tool in your mathematical journey. Here, we will delve into the step-by-step process of graphing linear equations, complete with practical examples, interactive elements, and a handy answer key to ensure you understand each concept thoroughly.
Understanding Linear Equations

A linear equation, in its simplest form, can be written as y = mx + b where:
- m represents the slope of the line, which dictates the direction and steepness.
- b is the y-intercept, the point where the line touches the y-axis.
Understanding these components is crucial as they are the keys to plotting linear graphs accurately.
Tools You Need
To graph linear equations effectively, you'll need:
- A sheet of graph paper or digital graphing software.
- A ruler or straightedge for precision.
- A pencil or digital pen tool for sketching and erasing if necessary.
- The equation itself!
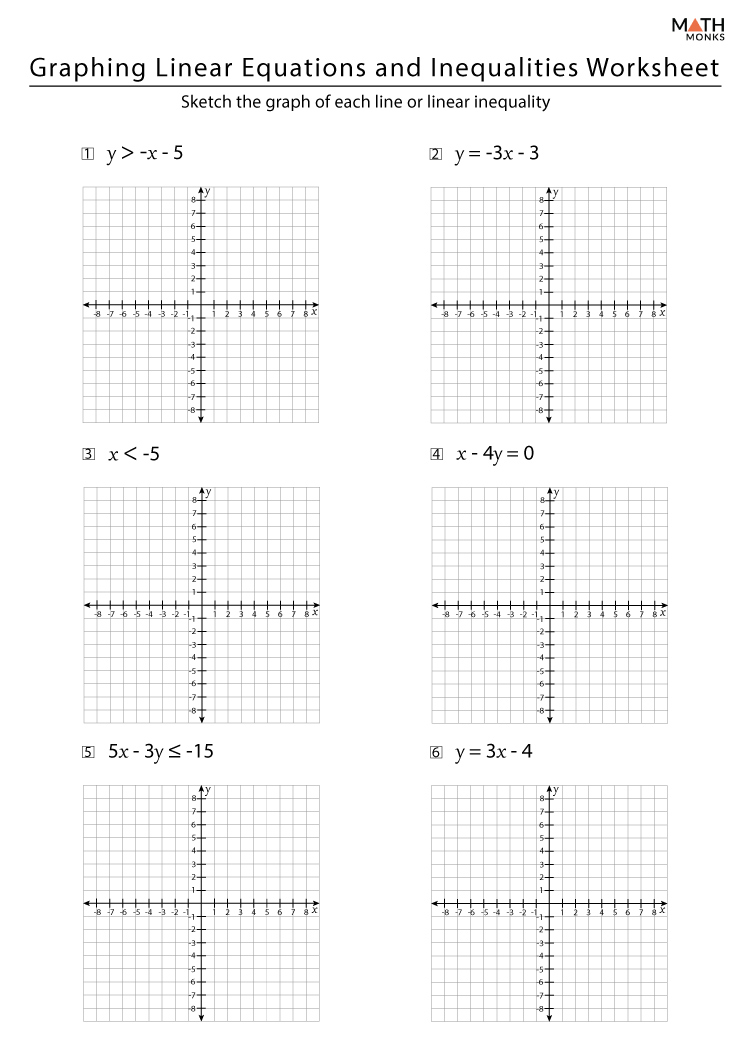
Graphing Linear Equations: Step-by-Step Guide

Finding the y-Intercept

Start by identifying the b in the equation. This tells you where to start drawing your line:
- Locate the y-intercept on the y-axis and mark this point.
- This point is your first coordinate, where x = 0.
Calculating Points

To plot the line, you need at least two points:
- Use the slope (m) to find another point. For example, if m = 3, from your y-intercept, go up 3 units and right 1 unit.
- Alternatively, use y = mx + b to calculate another point. If x = 2, then y = m*2 + b. Mark this second point.
📌 Note: When plotting, you can use either method or combine them for accuracy. Using the y-intercept and a single point calculated via the slope is often simplest.
Drawing the Line

Now, connect the dots:
- Draw a straight line through your two points. Use your ruler for precision.
- Extend the line slightly beyond the plotted points to show the line's direction.
Checking Your Work
Accuracy is key in math:
- Ensure the line passes through the y-intercept and any other calculated points correctly.
- Verify the line's steepness matches the slope's direction and magnitude.
Practical Example

Let's graph the equation y = 2x + 3:
- The y-intercept b is 3. Mark (0, 3).
- The slope m is 2. Go up 2 units and right 1 unit from the y-intercept to get to (1, 5).
- Draw a straight line passing through (0, 3) and (1, 5).
| Point | (x, y) |
|---|---|
| 1st | (0, 3) |
| 2nd | (1, 5) |

In summary, by understanding the fundamentals of linear equations, utilizing the right tools, and following a structured approach, you can graph lines with confidence. Remember, practice is the best teacher in math. Use this worksheet as a foundation to build your graphing skills, and soon, you’ll be plotting graphs in no time!
To aid your learning further, here’s an answer key for some commonly asked questions:
What if the slope of the line is negative?
+
If the slope is negative, the line will descend from left to right. For example, if m = -2, go down 2 units and right 1 unit from the y-intercept.
Can I use any other points to plot the line?

+
Yes, you can use any x-value to find the corresponding y-value. Plotting several points ensures accuracy, but two points are sufficient for drawing the line.
How can I check if my graph is correct?

+
Ensure the line passes through the y-intercept and maintains the correct slope. Use different x values to confirm y values align with your equation.
What if there’s no y-intercept in the equation?

+
If b is 0, the line passes through the origin (0, 0). Use the slope to find another point, or solve for other x and y values.