Worksheet Piecewise Functions
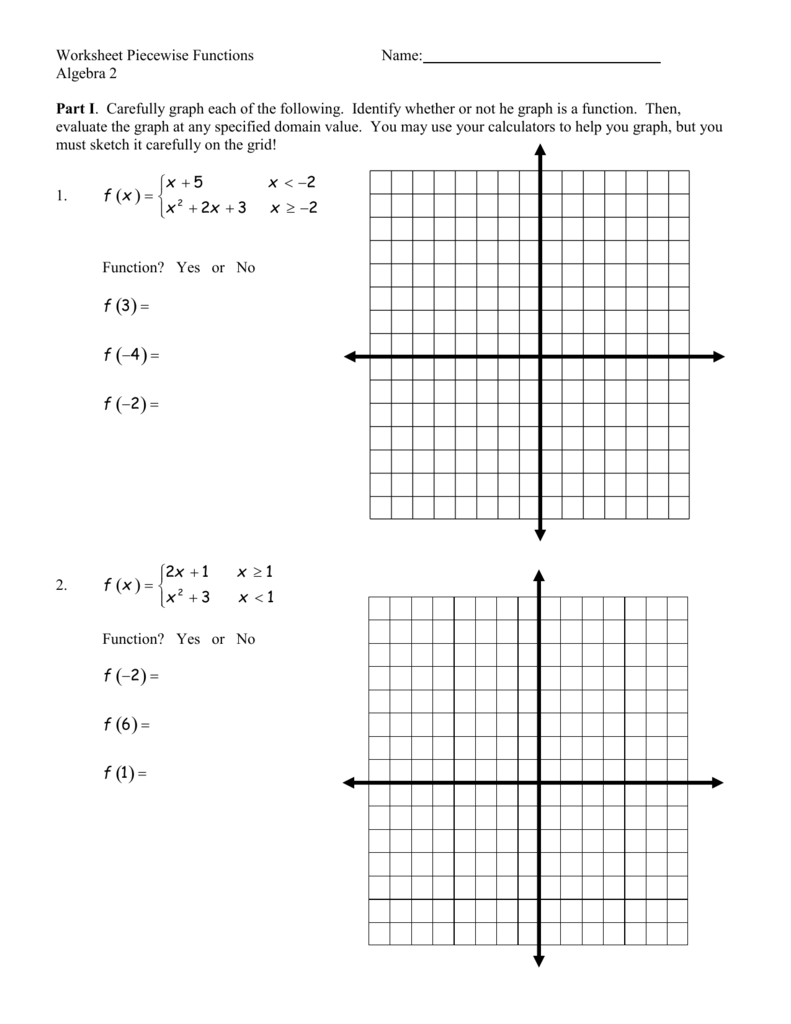
In mathematics, piecewise functions, often known as piecewise-defined or hybrid functions, are a fascinating and versatile tool for modeling complex, real-world phenomena. These functions are constructed by piecing together various segments, each defined by a different rule or expression, allowing for a flexible approach to describe scenarios that would be difficult to express using a single, continuous function.
Understanding Piecewise Functions
Piecewise functions allow us to define a function by different formulas over different intervals of its domain. Here’s how they look:
- The function might behave one way on one interval, then another way on the next.
- Each segment or “piece” is clearly defined, with conditions or constraints setting the boundaries for each part.
Let's dive into some core components:
Defining the Domain

Piecewise functions are typically defined over a piecewise domain, with conditions or constraints such as:
- x < 2
- 2 ≤ x < 5
- x ≥ 5
Each domain constraint provides a unique set of values for which the corresponding function segment applies.
Writing the Function

Here’s an example of a piecewise function:
- f(x) = { 2x - 1 if x < 2,
- f(x) = { x^2 if 2 ≤ x < 5,
- f(x) = { 5 if x ≥ 5.
This function describes different behaviors over three intervals of the x-axis:
- For x less than 2, the function is linear and increasing.
- Between x = 2 and x < 5, the function is quadratic and parabolas upward.
- For x greater than or equal to 5, the function is constant.
⚠️ Note: When defining piecewise functions, it's crucial to ensure that the segments are properly connected to avoid gaps or overlaps in the function's graph, which might lead to confusion in interpretation.
Evaluating Piecewise Functions

To evaluate a piecewise function:
- Identify the value of x.
- Determine which segment the x falls into based on the domain constraints.
- Use the corresponding rule for that segment to calculate the function’s value at x.
Example

Let’s evaluate f(x) at x = 4 for the function provided:
- x = 4 falls into the second segment (2 ≤ x < 5).
- Using the rule for this segment, f(4) = 4^2 = 16.
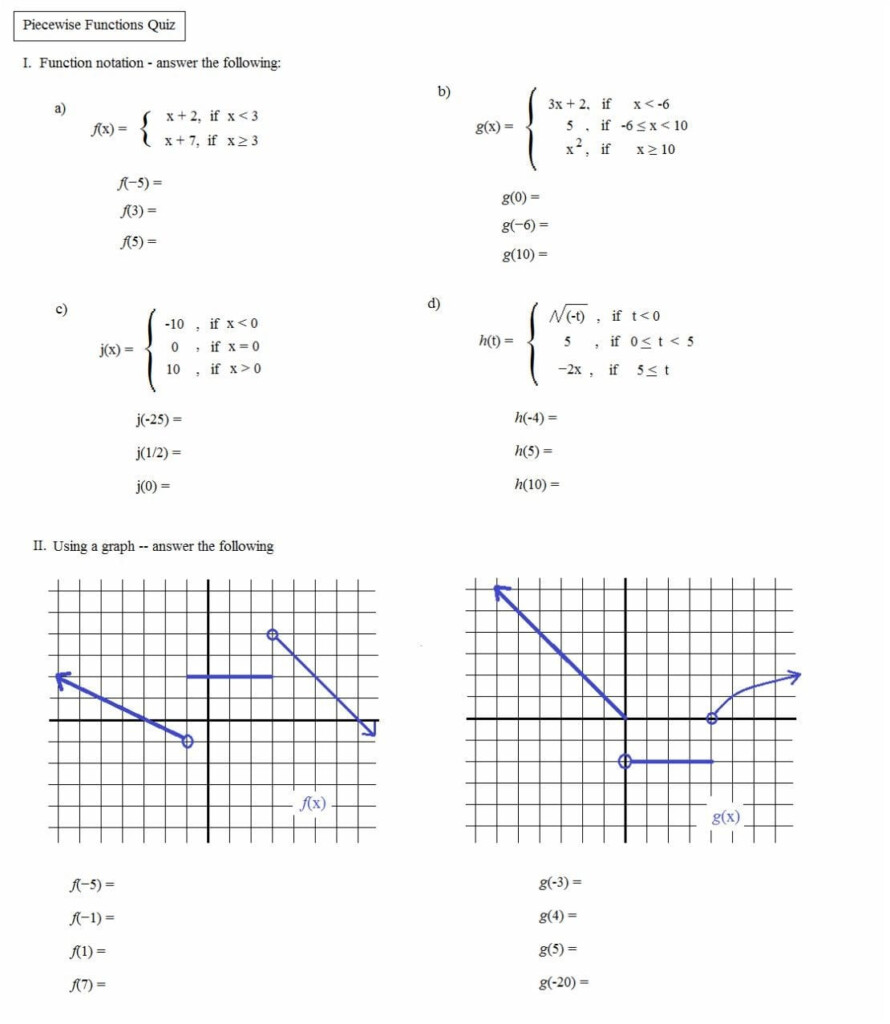
Graphing Piecewise Functions

The graphical representation of piecewise functions can be quite enlightening:
- Each segment is plotted separately for its respective domain.
- Use open or closed dots at the domain boundaries to denote how the function behaves at those points.
Visual Example

The function:
- f(x) = { 2x - 1 for x < 2,
- f(x) = { x^2 for 2 ≤ x < 5,
- f(x) = { 5 for x ≥ 5,
would look like:
- A straight line for x < 2
- A parabola opening upwards for 2 ≤ x < 5
- A horizontal line at y = 5 for x ≥ 5
📝 Note: Ensure that the graph includes all segments and that endpoints are marked correctly, open or closed, to reflect the domain constraints accurately.
Real-World Applications

Piecewise functions find applications in many fields:
- Economics: Piecewise linear functions can model tax brackets, where the tax rate changes at different income levels.
- Engineering: A circuit might have different behaviors based on the input voltage or current levels.
- Transportation: Toll prices that vary based on time or distance traveled can be modeled using piecewise functions.
The versatility of piecewise functions allows them to adapt to various scenarios where conditions change abruptly, making them an essential tool in mathematics and beyond.
🌍 Note: In real-world applications, piecewise functions are often used to simplify complex models by breaking them down into more manageable, behavior-specific segments.
Advanced Concepts in Piecewise Functions
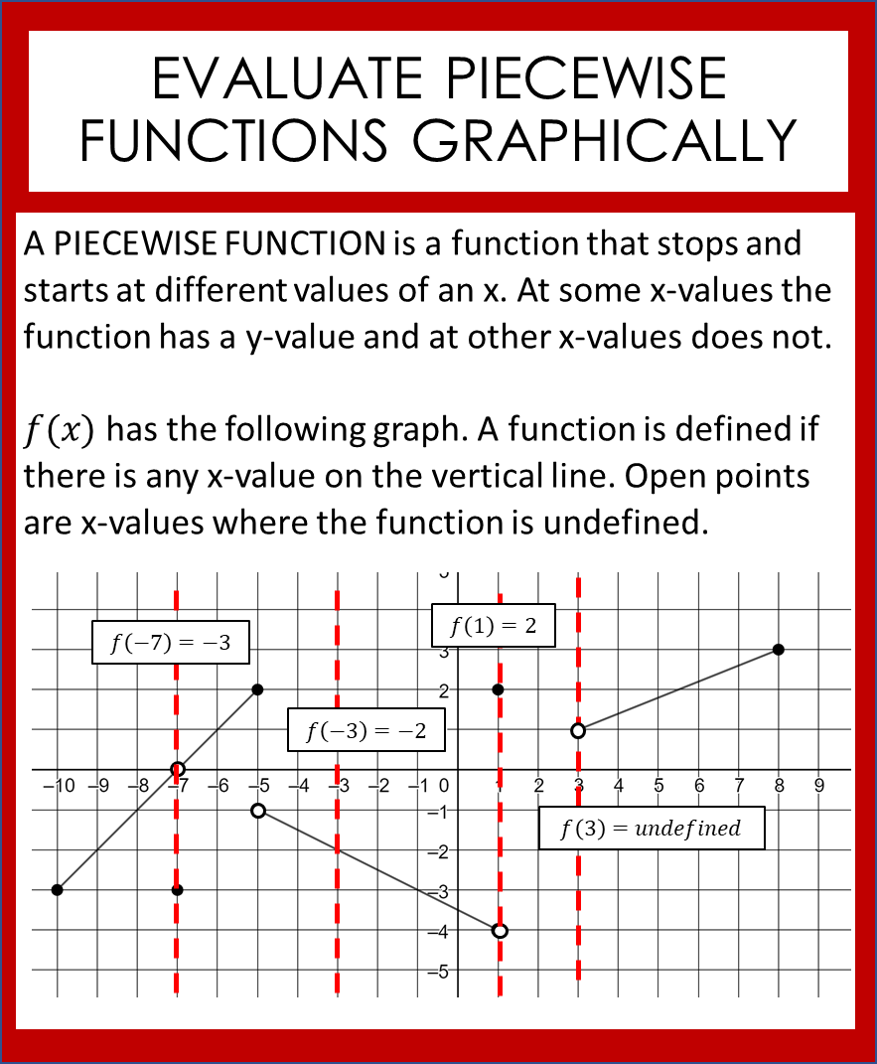
Piecewise functions can encompass more than just linear or quadratic segments:
- Step Functions: They are like a staircase, often used to model processes with discrete changes.
- Discontinuous Functions: Sometimes functions are not defined at certain points or have jumps, like the floor function or ceiling function.
- Continuity: Exploring continuity at the points where different segments meet provides insights into function behavior and smoothness.
These advanced topics enrich our understanding and allow for more complex modeling.
In essence, piecewise functions are a powerful mathematical tool that allow us to describe and analyze a variety of scenarios where traditional, single-formula functions fall short. They enable us to piece together different mathematical expressions to match real-world conditions, thus providing a practical bridge between theory and application. Whether you're calculating tax rates, designing electronic circuits, or solving optimization problems, understanding how to work with piecewise functions can significantly enhance your analytical capabilities.
What is the difference between a piecewise and a regular function?

+
A regular function has a single rule or expression that applies over its entire domain, while a piecewise function consists of multiple segments, each with its own rule, over different intervals of the domain.
How do you know if a function is piecewise?

+
A function is piecewise if its definition changes at different points in its domain, typically denoted by the use of conditions like “if x < a,” “if a ≤ x < b,” or similar expressions that indicate a change in behavior over different parts of the domain.
Can piecewise functions have infinite segments?

+
Yes, in theory, a piecewise function can have an infinite number of segments. For example, trigonometric functions or wave patterns might be approximated by many segments, each representing a different part of a cycle.