7 Tips for Mastering Inscribed Angles and Arcs in Geometry

Geometry, the study of shapes, sizes, and properties of figures and spaces, offers numerous fascinating concepts that are both fun and challenging to learn. Among these, the relationship between inscribed angles and arcs stands out as a particularly intriguing area. Mastering these concepts can not only bolster your understanding of geometry but also lay a strong foundation for advanced mathematical studies. Here are seven tips to help you master inscribed angles and arcs in geometry:
Understanding the Basics

The first step to mastering inscribed angles and arcs is understanding their definitions and relationships:
- Inscribed Angle: An angle whose vertex lies on the circumference of a circle and whose sides intersect the circle at two points on the circumference.
- Arc: A portion of the circumference of a circle.
🔍 Note: The measure of an inscribed angle is always half the measure of the intercepted arc.
Visualizing Through Diagrams


Diagrams are crucial in geometry. Visualizing inscribed angles and arcs through well-labeled diagrams can make these abstract concepts more tangible:
- Draw circles and mark angles clearly to understand their placement and measurement.
- Use different colors or patterns to differentiate between different arcs.
Practice with Examples

Engaging with varied examples is one of the most effective ways to learn:
- Solve problems where you calculate the measures of inscribed angles given the arc length.
- Work backward by determining arc measures from given inscribed angles.
💡 Note: Always check your work by comparing your calculated values with the properties of circles.
Explore Interactive Geometry Software

Technology can enhance your learning experience:
- Use tools like GeoGebra or other interactive geometry programs to dynamically explore angles and arcs.
- Experiment with different angles and observe how the properties change.
Master the Theorems

Knowing the key theorems related to inscribed angles and arcs is essential:
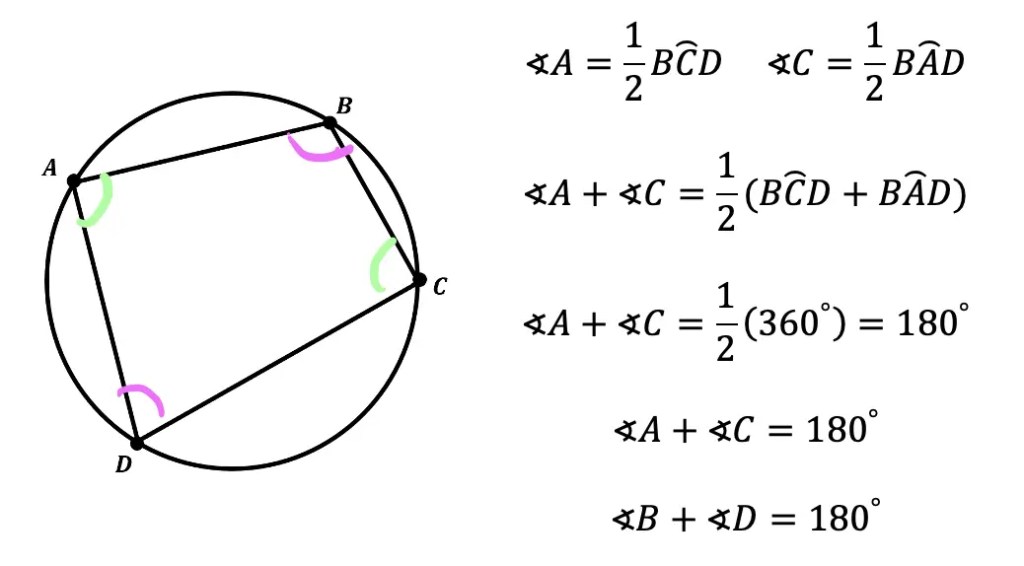
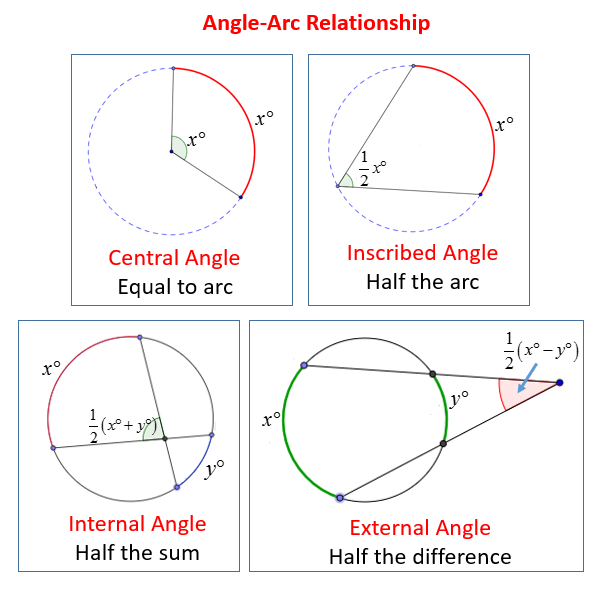
- Inscribed Angle Theorem: The measure of an inscribed angle is half the measure of the intercepted arc.
- Cyclic Quadrilateral Theorem: Opposite angles of a cyclic quadrilateral sum up to 180 degrees.
- Angle at the Center Theorem: An angle at the center of a circle is twice any angle at the circumference subtended by the same arc.
Create a Cheat Sheet

Summarize the key points on a cheat sheet:
| Theorem | Description |
|---|---|
| Inscribed Angle Theorem | Inscribed angle = 1⁄2 Intercepted arc |
| Cyclic Quadrilateral | Opposite angles sum to 180° |
| Angle at the Center | Central angle = 2x Inscribed angle |

Teach What You Learn
Teaching someone else is one of the best ways to solidify your own understanding:
- Explain to a friend or peer how inscribed angles relate to arcs.
- Create a tutorial or lesson plan on this topic.
📝 Note: Teaching forces you to clarify your own understanding and often highlights areas where further learning is required.
In conclusion, mastering inscribed angles and arcs involves a blend of understanding theory, practical application through problem-solving, and leveraging tools and techniques that enhance learning. By starting with the basics, using visual aids, engaging with technology, understanding theorems, creating a reference material, and teaching others, you can gain a deep and thorough grasp of these geometric concepts. These strategies not only help in mastering geometry but also in developing a broader, more nuanced mathematical understanding.
What is the difference between a central angle and an inscribed angle?

+
A central angle is an angle whose vertex is at the center of the circle, and its sides pass through two points on the circumference. An inscribed angle has its vertex on the circle, with its sides intersecting the circle at two points, creating an arc. The key difference is that a central angle measures the entire intercepted arc, while an inscribed angle measures half of it.
How does an inscribed angle help in solving for unknown angles or arcs?

+
The inscribed angle theorem allows us to find unknown angles or arc lengths by providing a direct relationship: the angle at the circumference is half the angle at the center subtended by the same arc. This relationship is particularly useful in solving complex geometric problems where direct measurement isn’t possible.
Can inscribed angles be used in polygons?

+
Yes, inscribed angles are also applicable within polygons inscribed in a circle. For instance, in a cyclic quadrilateral, opposite angles sum up to 180 degrees, which can help in solving various geometrical problems involving such polygons.
Why is it beneficial to use interactive tools like GeoGebra for learning?
+
Interactive tools like GeoGebra allow for dynamic manipulation of geometric shapes, which can visually and kinesthetically reinforce understanding. This hands-on approach helps in discovering relationships and properties in real-time, making abstract concepts more concrete and understandable.



