5 Essential Tips for Pre-Calc Limits Mastery

Calculus can seem like an intimidating subject, particularly when you start diving into the concept of limits. Understanding limits is crucial because they form the foundation for derivatives, integrals, and other key elements of calculus. Whether you're prepping for a big exam or just trying to grasp the basics, mastering limits in pre-calculus can give you a substantial advantage. Here are five essential tips to help you conquer this fundamental calculus concept:
1. Understand the Conceptual Framework

Before you jump into the computations, it’s important to grasp what limits actually mean:
- Intuition: Think of limits as a way to describe the behavior of functions as they approach a certain point.
- Precision: Limits provide a tool to rigorously define rates of change and accumulation, two concepts at the heart of calculus.
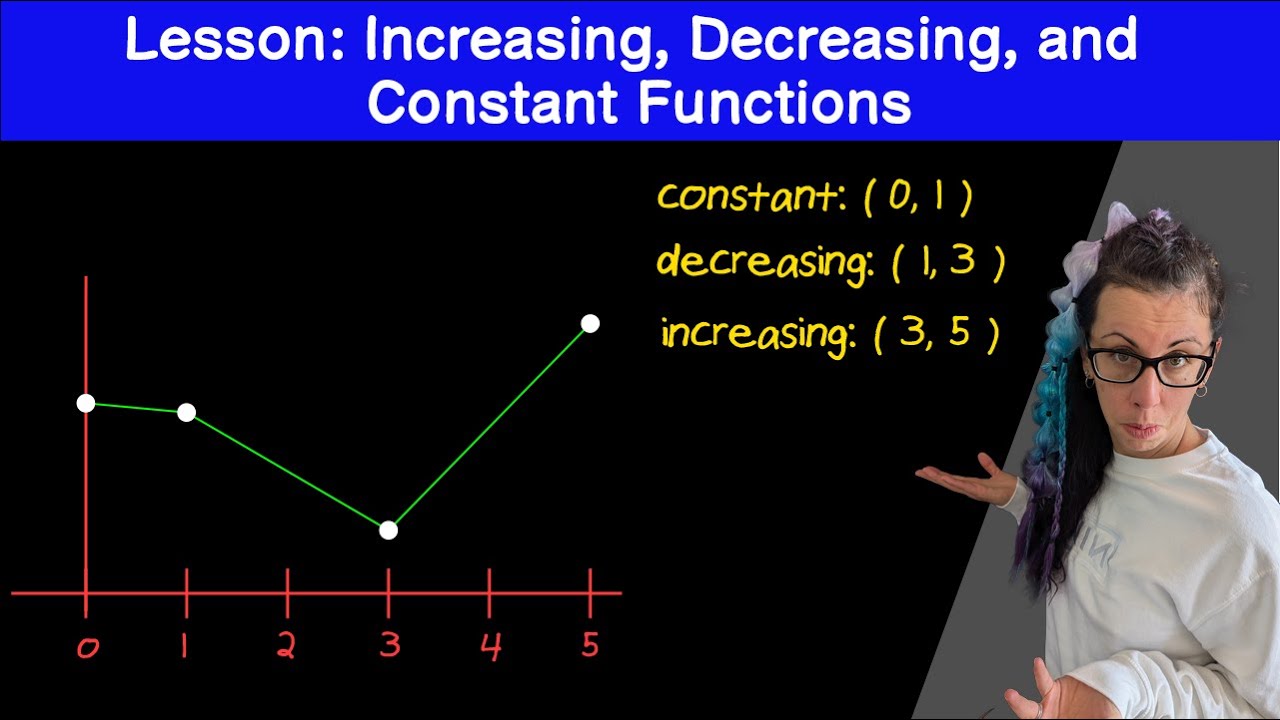
- Visualization: Graphically visualizing how a function behaves near a certain value can significantly aid in understanding limits. Use graphing tools or sketch functions by hand to see how they approach limits from both directions.
2. Master the Notation

Limit notation can be confusing if you’re not familiar with it:
- The lim symbol: When you see lim f(x) as x approaches a, you’re looking at what value f(x) gets close to as x gets very close to, but not equal to, a.
- One-sided limits: Sometimes, limits from the left (lim f(x) as x approaches a-) or from the right (lim f(x) as x approaches a+) are different. These are crucial for understanding discontinuous functions.
- Infinite Limits: When f(x) grows or decreases without bound, we use ±∞ to indicate the behavior.
⚠️ Note: Understanding notation will save you from common errors when interpreting or computing limits.
3. Utilize Fundamental Theorems

Calculus has several theorems that can simplify your approach to limits:
- Squeeze Theorem: If a function f(x) is sandwiched between g(x) and h(x), and g(x) and h(x) approach the same limit, then f(x) does too.
- Limit Properties: Addition, subtraction, multiplication, and division of limits (when limits exist) have straightforward properties.
- Intermediate Value Theorem: A function continuous on an interval must take on every value between the function values at the endpoints. This helps in proving the existence of limits.
4. Practice with Standard Forms

Here are some common limit forms to practice:
| Function | Limit |
|---|---|
| sin(x) / x as x → 0 | 1 |
| (1 + x)^1/x as x → 0 | e |
| ln(1 + x) / x as x → 0 | 1 |
| (e^x - 1) / x as x → 0 | 1 |
These forms come up often, so mastering them can give you a head start on complex problems.
📚 Note: Knowing these standard forms can streamline your problem-solving process by allowing you to directly apply results instead of re-deriving them.
5. Develop Problem-Solving Strategies

Solving limit problems often requires a strategic approach:
- Direct Substitution: Sometimes the limit can be found simply by plugging the value into the function. If the function is undefined at that point, this might not be possible.
- Rationalization: For expressions with radicals or complex fractions, rationalizing the numerator or denominator can help.
- L’Hôpital’s Rule: Useful for indeterminate forms like 0/0 or ∞/∞, apply this rule after you’ve tried simpler methods.
- Graphical Analysis: Looking at a graph of the function can provide insight into the behavior near the limit point.
- Continuity Analysis: If the function is continuous at the point of interest, the limit equals the function value at that point.
By now, you've traversed through some essential strategies for mastering pre-calculus limits. Remember, limits are not just about solving problems; they are about understanding the very essence of how functions behave. The key takeaway is that limits are the gateway to calculus, providing the language and tools necessary to analyze how functions evolve and interact. Embrace these tips, practice consistently, and don't be afraid to explore different approaches. Limits might seem like a daunting topic initially, but with patience and practice, you'll find they unlock a world of mathematical possibilities.
What is the importance of limits in calculus?

+
Limits are fundamental to calculus because they help define derivatives, integrals, and continuity, which are core concepts. They provide a precise way to understand how functions behave as they approach specific points or conditions.
How can I remember limit properties?

+
To remember limit properties, create mnemonic devices or use visual aids. For example, visualize the arithmetic operations on limits as similar to those on constants: addition, subtraction, multiplication, and division (with restrictions).
What are some common mistakes when solving for limits?

+
Common mistakes include ignoring indeterminate forms, not considering one-sided limits, not using theorems like L’Hôpital’s rule appropriately, and forgetting that the limit of a product or quotient is not necessarily the product or quotient of the limits if one or both are undefined.