Trigonometry Pile Up Worksheet Solutions Unveiled

Introduction to Trigonometry

Trigonometry, often referred to as the study of triangles, plays a pivotal role in various fields including engineering, physics, and even music. It introduces concepts like sine, cosine, and tangent, which are not just abstract functions but have real-world applications. This guide aims to shed light on solving trigonometry pile-up worksheets, offering insights into these often challenging yet essential problems.
Understanding Trigonometry Basics

Before we delve into complex worksheets, a quick recap on the fundamentals can set the stage for deeper understanding:
- Sine (sin) - The ratio of the length of the opposite side to the hypotenuse.
- Cosine (cos) - The ratio of the length of the adjacent side to the hypotenuse.
- Tangent (tan) - The ratio of the length of the opposite side to the adjacent side.
- Hypotenuse - The longest side of a right-angled triangle.
Solving Pile-Up Worksheets

Trigonometry pile-up worksheets present multiple problems where one answer leads to the setup of the next, making it crucial to solve each problem accurately to avoid a "pile-up" of errors. Here's how you can tackle these worksheets effectively:
Step-by-Step Solving Process
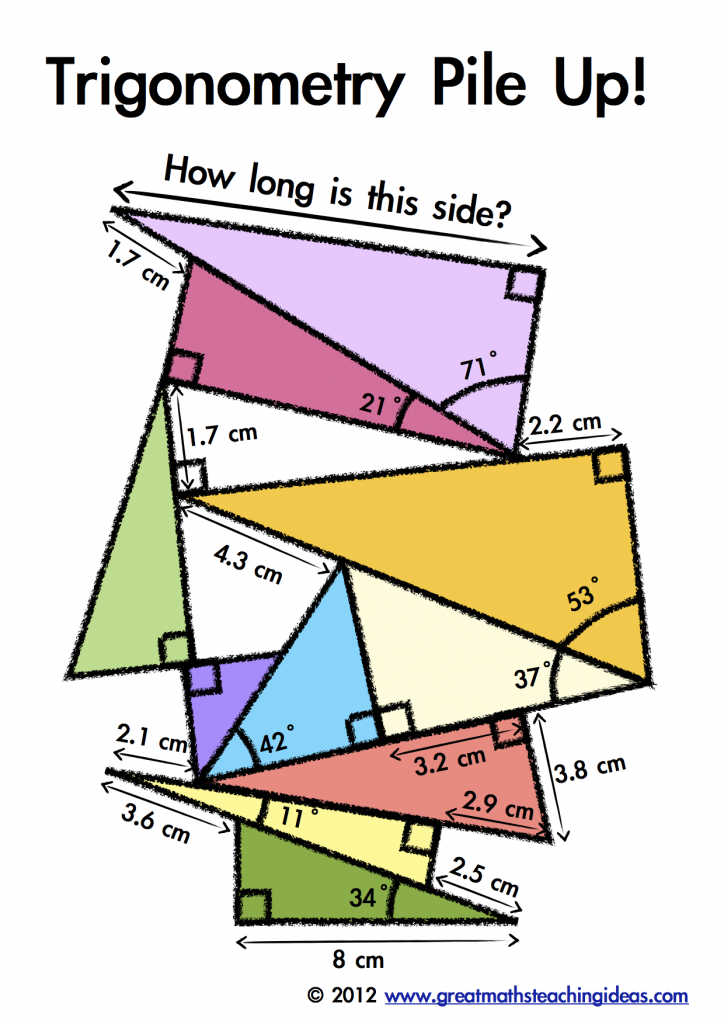
Let's walk through the typical process of solving a trigonometry pile-up worksheet:
- Identify the Problem: Carefully read the problem statement. What are you given? What are you asked to find?
- Label Your Triangle: Assign variables to the sides or angles of your triangle. Use a, b, c for sides, and A, B, C for angles.
- Set Up the Equation: Using trigonometric identities or the Pythagorean theorem, set up the equation that relates known values to the unknown ones.
- Solve the Equation: Solve for the unknown using algebraic methods. Ensure you're using the correct inverse trigonometric function.
- Check Your Answer: Trigonometric identities can often confirm or reject your solution.
- Move to the Next Problem: Use the solution from the previous step as the input for the next problem in the pile-up.
🏗️ Note: Trigonometry requires precision; a small error can lead to a cascade of mistakes through the pile-up process.
Example Solution of a Pile-Up Worksheet

Here's an example to illustrate the pile-up process:
Given: A right triangle with an angle of 30 degrees, and the hypotenuse c is 10 cm. Find the length of the side opposite to the 30-degree angle.
We know:
- sin(30°) = a/c
- sin(30°) = 0.5
So, we can set up the equation:
0.5 = a/10 ⟹ a = 5 cm
Now, let's move to the next problem in our pile-up:
Using a as the side adjacent to another angle, and knowing that the sum of angles in a triangle is 180°, we need to find the other side of the triangle.
| Step | Description |
|---|---|
| 1 | Identify the Problem |
| 2 | Label Your Triangle |
| 3 | Set Up the Equation |
| 4 | Solve the Equation |
| 5 | Check Your Answer |
| 6 | Move to the Next Problem |

This example shows how each problem builds on the solution of the previous one. This chain reaction ensures that mastering each step is essential for overall success in the worksheet.
Advanced Trigonometric Concepts

As you delve deeper into trigonometry, you'll encounter more complex problems involving:
- Inverse Trigonometric Functions - arcsin, arccos, and arctan help solve for angles given side ratios.
- Double Angle Formulas - For problems involving twice an angle.
- Sum and Difference Identities - Useful for combining angles or breaking down complex trigonometric expressions.
Understanding these concepts allows you to tackle problems where you must first use basic trigonometry to find known values, then apply these advanced formulas to complete the worksheet.
Final Thoughts on Trigonometric Worksheets

As you work through trigonometry pile-up worksheets, remember that precision is key. A small error in calculation can lead to a significant deviation from the correct solution. Each problem in a pile-up requires careful handling, with each answer setting the stage for the next. Through practice, you'll grow confident in using trigonometric functions not just as abstract concepts, but as tools to solve real-world problems. This journey will improve your analytical skills, enhance your problem-solving abilities, and deepen your understanding of the interconnected nature of mathematical solutions.
What makes pile-up worksheets different from regular trigonometry problems?

+
Pile-up worksheets require sequential problem-solving where each solution sets up the conditions for the next problem, making accuracy critical.
How can I avoid common mistakes in trigonometry pile-ups?

+
Use precise calculations, double-check your trigonometric identities, and always verify your answers using alternative methods or identities.
Is trigonometry only useful for academic purposes?

+
No, trigonometry has practical applications in architecture, physics, engineering, music, computer graphics, and more, making it an essential tool for understanding the world around us.



