5 Ways to Solve Triangle Congruence Worksheet 1

Triangles are a fundamental element in geometry, often found in problems concerning shape, size, and symmetry. Understanding how triangles are congruent - essentially identical in shape and size - is critical for a wide array of geometric applications. Here, we will explore five effective strategies to help you master triangle congruence when tackling Triangle Congruence Worksheet 1.
Understanding Triangle Congruence

Before diving into the strategies, let's quickly review what triangle congruence means:
- Definition: Two triangles are congruent if all their corresponding angles and sides are equal.
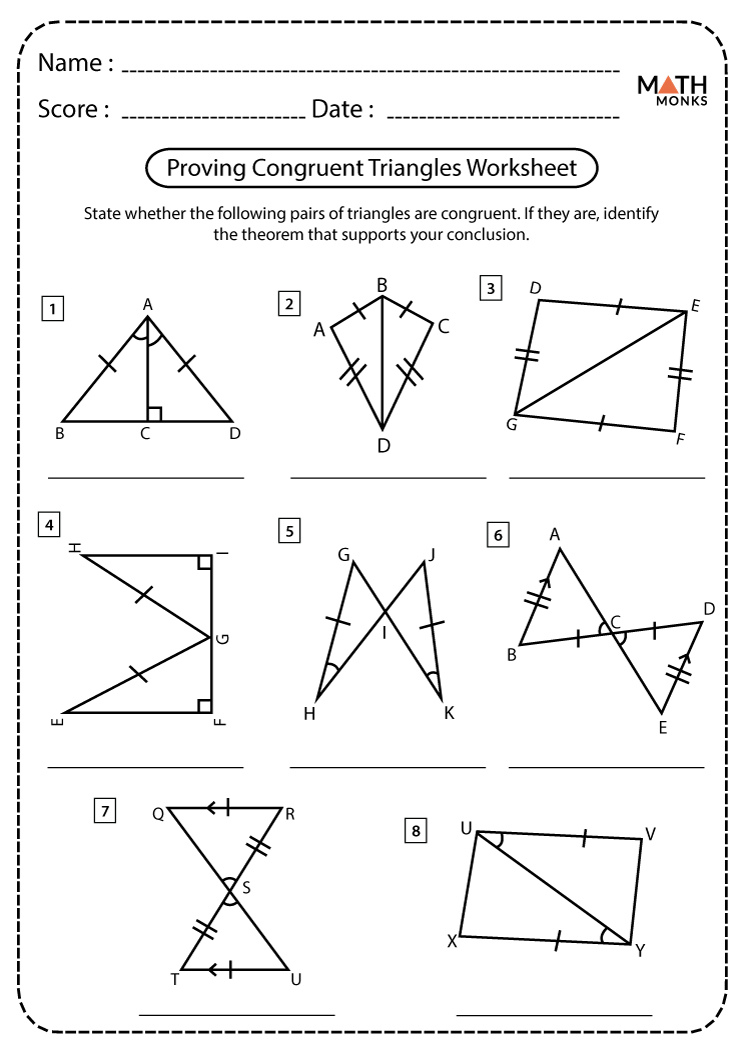
- Common Criteria for Congruence: There are five main methods to prove triangles are congruent, known as SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), AAS (Angle-Angle-Side), and HL (Hypotenuse-Leg) for right triangles.

Strategy 1: Visualize and Compare

One of the first steps in solving a triangle congruence worksheet is to:
- Visualize each triangle from the problem.
- Draw them if necessary, marking any given angles and side lengths.
- Compare the triangles side by side to see if they appear to match any of the congruence rules.
Remember that sometimes, the triangles might be rotated or reflected, so use rotation or reflection to bring them into a standard orientation for easier comparison.
📌 Note: If two triangles are not congruent after simple rotations or reflections, they are not congruent at all.
Strategy 2: Use Congruence Theorems

Once you've visualized and possibly drawn the triangles, apply the following congruence theorems:
- SSS Congruence: If three sides of one triangle are equal to the corresponding three sides of another, the triangles are congruent.
- SAS Congruence: If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, the triangles are congruent.
- ASA Congruence: If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, they are congruent.
- AAS Congruence: Similar to ASA, but the side is non-included.
- HL Congruence: For right triangles, if the hypotenuse and one leg of one right triangle are equal to the hypotenuse and one leg of another right triangle, the triangles are congruent.
Strategy 3: Apply Algebraic Proofs
When visual and theorem-based methods don't suffice:
- Set up equations using the given sides and angles.
- Solve the equations to check if the triangles are congruent.
- Algebraic manipulation can provide insight into whether two triangles have all sides and angles equal.
📌 Note: Be cautious with assumptions and check that you have indeed proven all corresponding parts equal before concluding congruence.
Strategy 4: Employ Indirect Proofs

Sometimes, direct proofs are not immediately apparent:
- Use a method of contradiction. Assume the triangles are not congruent.
- Then, through logical deduction, show that this assumption leads to a contradiction.
- Hence, proving that the triangles must be congruent.
Strategy 5: Practice with Pattern Recognition

Geometry often involves recognizing patterns:
- Look for triangles within shapes or even within other triangles.
- Use known properties like properties of isosceles and equilateral triangles to deduce congruence.
- Recognize and leverage the fact that congruent triangles can be used to prove various other geometric theorems.
By practicing with various worksheets, you'll become adept at quickly identifying congruent triangles in different settings.
| Strategy | Description |
|---|---|
| Visualize and Compare | Draw and compare triangles visually for congruence. |
| Use Congruence Theorems | Apply SSS, SAS, ASA, AAS, or HL rules to prove congruence. |
| Apply Algebraic Proofs | Use algebra to prove sides and angles are equal. |
| Employ Indirect Proofs | Prove congruence through contradiction. |
| Pattern Recognition | Recognize triangles and congruent properties within patterns. |

The essence of mastering triangle congruence lies in a balanced approach between visual interpretation and formal proof methods. As you work through Triangle Congruence Worksheet 1, you'll notice that each strategy builds upon the last, providing a comprehensive toolkit for solving problems. Remember, not every worksheet will require all strategies, but familiarity with each will boost your problem-solving capabilities in geometry and beyond.
What is the difference between congruence and similarity in triangles?

+
Congruent triangles are identical in both shape and size, meaning all corresponding sides and angles are equal. Similar triangles, on the other hand, have the same shape but not necessarily the same size. Their corresponding angles are equal, but the sides are proportional.
Can you prove triangle congruence without using all sides or angles?

+
Yes, through theorems like ASA or AAS, you can prove triangles congruent by using two angles and a non-included or included side. HL also allows for congruence proof using just the hypotenuse and one leg in right triangles.
How does understanding triangle congruence benefit real-world applications?

+
Understanding triangle congruence is crucial in fields like engineering, architecture, and surveying for ensuring structural stability, precise measurements, and correct alignments. It’s also used in computer graphics, navigation systems, and many other technologies where shape and orientation are important.
What if my triangles don’t match any of the five congruence rules?

+
If your triangles do not match the established congruence rules, they are not congruent. You might need to recheck your initial givens or consider alternative geometric theorems or properties.