Master Triangle Congruence with Our Ultimate Worksheet Guide
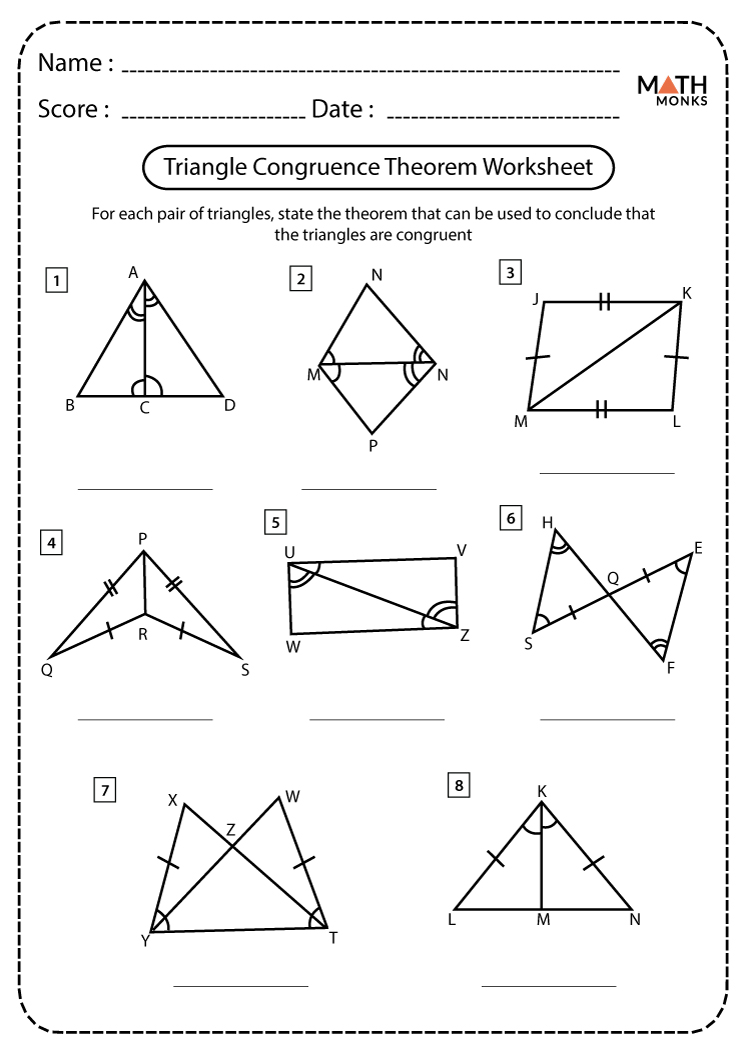
Triangles are the simplest geometric shapes, yet their study provides deep insight into geometry and real-world applications. Whether you're a student tackling geometry or a professional needing to use geometric principles, understanding triangle congruence is key. This comprehensive guide will delve into various methods for proving triangle congruence, offering you the ultimate worksheet to master these concepts.
What is Triangle Congruence?

Triangle congruence occurs when two triangles have all corresponding sides and angles equal. When triangles are congruent, they are identical in shape and size, and all corresponding parts of congruent triangles are congruent (CPCTC).
Methods of Proving Triangle Congruence

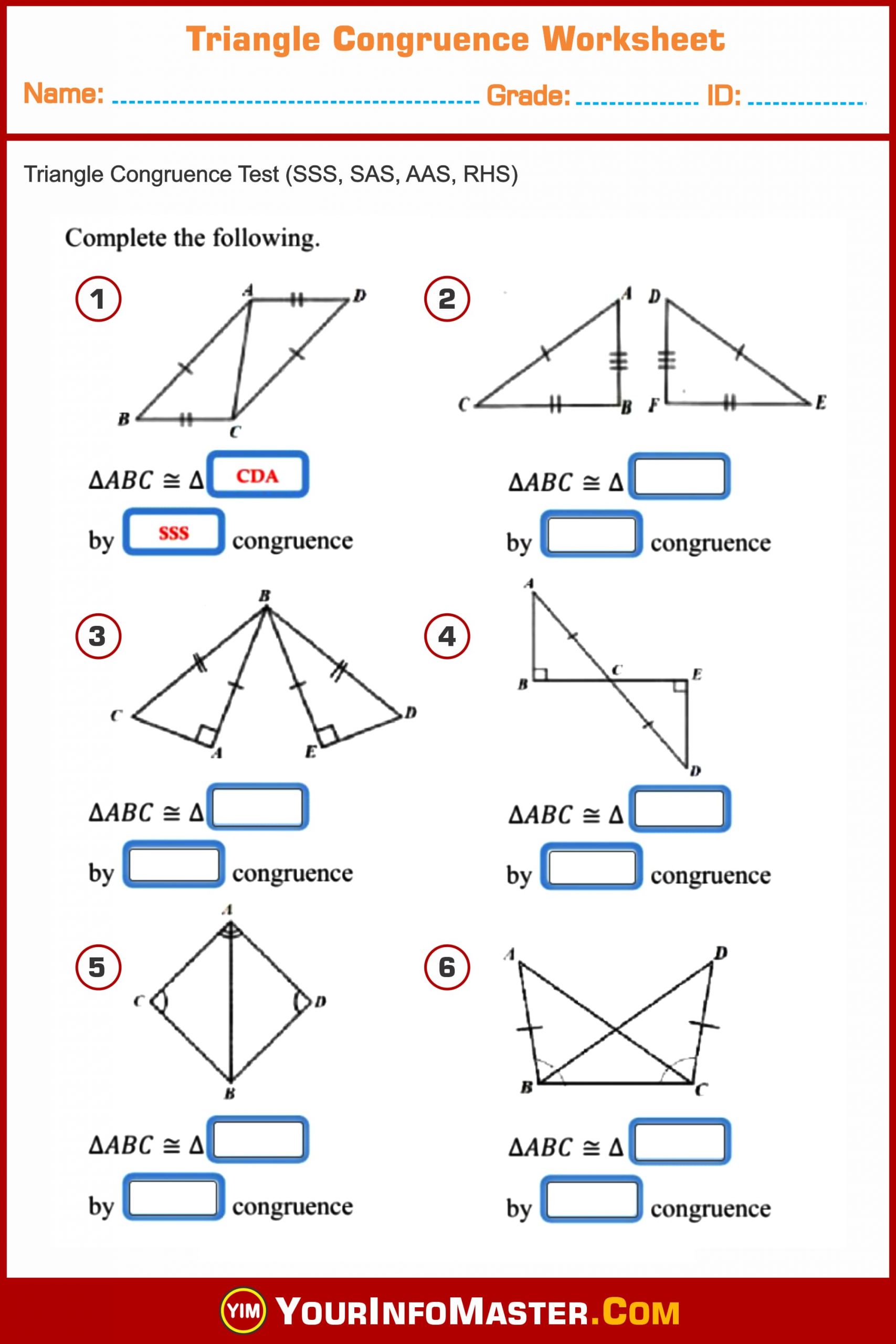
- SSS (Side-Side-Side): If all three sides of one triangle are equal to the corresponding sides of another triangle, the triangles are congruent.
- SAS (Side-Angle-Side): If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, the triangles are congruent.
- ASA (Angle-Side-Angle): If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, the triangles are congruent.
- AAS (Angle-Angle-Side): Similar to ASA but includes a non-included side. Two angles and any side of one triangle are equal to two angles and the corresponding side of another triangle.
- HL (Hypotenuse-Leg) in Right Triangles: If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle, the triangles are congruent.
Interactive Triangle Congruence Worksheet

Let’s explore how to use an interactive worksheet to enhance your understanding:
Worksheet Overview

| Section | Description |
|---|---|
| Introduction | Basic theory of triangle congruence and its relevance. |
| Step-by-Step Problems | Solve problems categorized by the method of proof. |
| Advanced Exercises | Challenge yourself with complex triangles and proofs. |

How to Use the Worksheet

- Start with SSS Congruence problems:
- Identify the sides you know are congruent.
- Match the sides of both triangles.
- Prove congruence using the SSS theorem.
- Move to SAS Congruence examples:
- Identify two sides and the included angle.
- Use these to prove congruence.
- Work on ASA, AAS, and finally HL proofs:
- Identify the given parts.
- Apply the respective theorems to prove congruence.
Common Mistakes to Avoid

- Not labeling the triangles or sides properly.
- Assuming angles are congruent without proper proof.
- Misapplying congruence theorems, especially for non-right triangles.
📚 Note: Remember that the order of vertices in both triangles must match when using congruence postulates.
Why Master Triangle Congruence?

Understanding triangle congruence is crucial for several reasons:
- Geometry Foundations: It forms the basis for many geometric proofs and properties.
- Problem-Solving Skills: It develops critical thinking and logical reasoning.
- Practical Applications: From architecture to engineering, congruent triangles appear in real-world designs.
🌟 Note: Congruence helps in simplifying complex geometric structures into manageable parts.
Enhancing Your Learning Experience
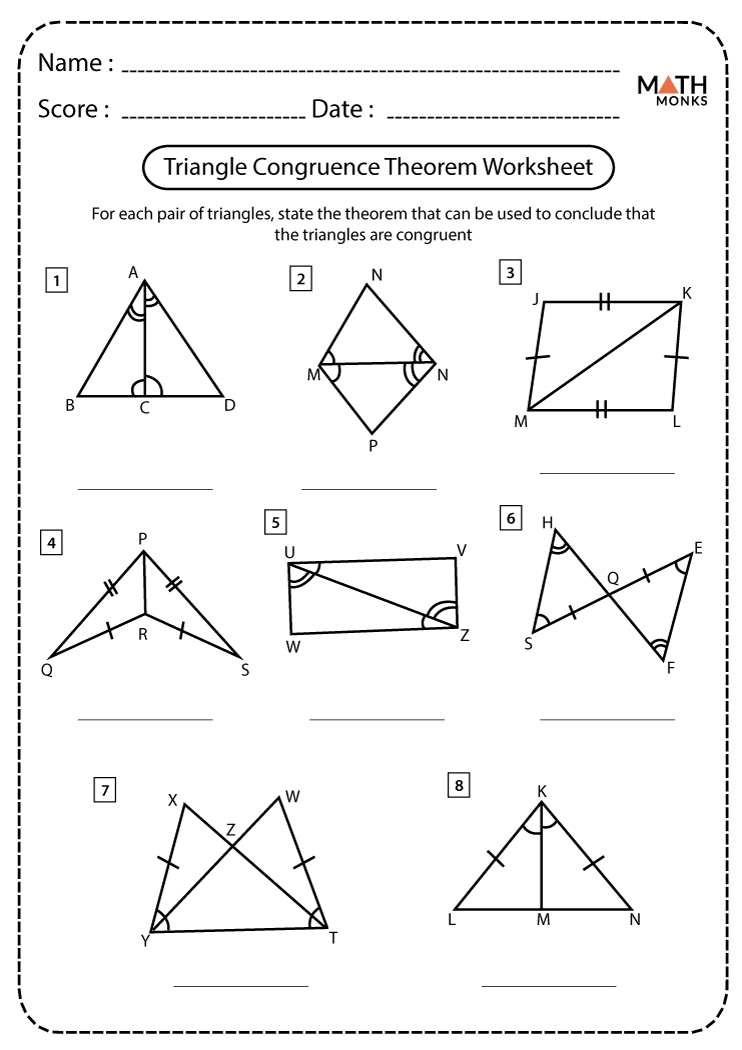
Here are some tips to make learning triangle congruence more engaging:
- Use Visual Aids: Draw or use geometric software to visualize triangle relationships.
- Practice Regularly: Incorporate the worksheet into your daily study routine.
- Discuss with Peers: Engage in group study sessions to clarify doubts and share insights.
💡 Note: Hands-on activities with physical triangle models can significantly enhance your understanding.
In summary

Triangle congruence is a foundational concept in geometry that impacts not only mathematical understanding but also practical applications. By mastering the methods of proving congruence through this ultimate worksheet guide, you’ve equipped yourself with valuable tools for problem-solving, spatial reasoning, and even real-world design. Each method of proving congruence provides a unique perspective on how triangles can be identical, highlighting the intricate beauty of geometric relationships. Regular practice, visual aids, and interactive learning will ensure you retain this knowledge, making triangle congruence a concept you’ll find intuitive and second nature in your geometric explorations.
What is the main difference between SAS and AAS?

+
The key difference is the placement of the angle in relation to the sides. In SAS, the angle is included between the two sides, whereas in AAS, the angle is not included, and the side corresponding to this angle can be any of the triangle’s sides.
Can congruence be applied to polygons other than triangles?
+
Congruence applies to all polygons, but the complexity increases with the number of sides. For polygons with more than three sides, you would need to ensure that all corresponding sides and angles are congruent.
How do you know if triangles are congruent without all the measurements?

+
If enough information is given according to any of the congruence postulates (SSS, SAS, ASA, AAS, or HL for right triangles), you can determine congruence without needing every measurement. For instance, if two sides and the angle between them are the same, then by SAS, the triangles are congruent.