Absolute Value Equations: Worksheet and Solutions Guide
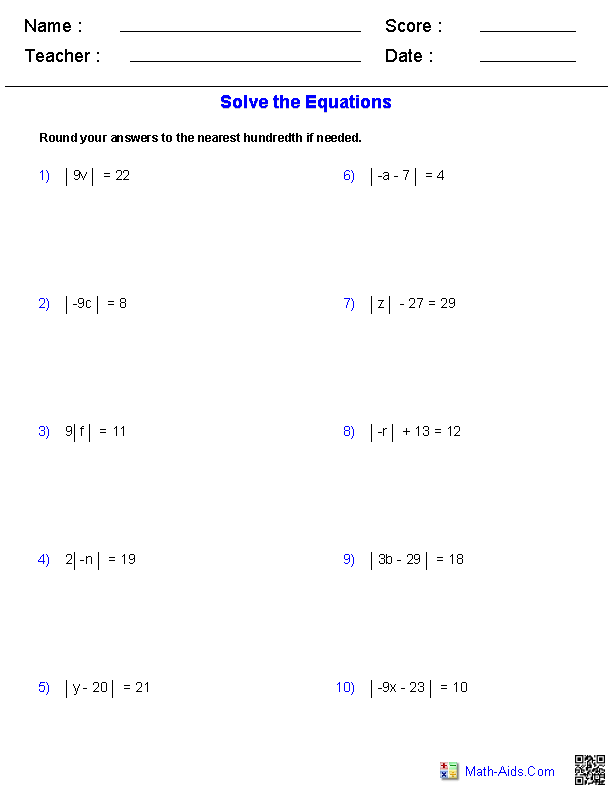
In the realm of algebra, mastering the concept of absolute value is fundamental. It's a concept that students often grapple with due to its unique properties and how it changes the behavior of expressions. Today, we'll delve into absolute value equations, explore how to solve them, and provide a detailed worksheet with solutions. This guide will not only help you understand the mechanics of these equations but also equip you with the tools to teach or learn this topic effectively.
Understanding Absolute Value


At its core, absolute value refers to the distance from a number to zero on the number line, disregarding direction. Represented by the symbols ||, the absolute value of a number x is defined as:
- |x| = x, if x is positive or zero
- |x| = -x, if x is negative
The Dual Nature of Absolute Value Equations

Solving an absolute value equation involves recognizing that there can be two possible solutions for any non-zero expression inside the absolute value. Here’s how:
- If |ax + b| = c, then:
- ax + b = c
- ax + b = -c
This duality arises because the absolute value equation requires us to consider both the positive and negative scenarios to cover all possible solutions.
Solving Absolute Value Equations: A Step-by-Step Guide

To master the solving of absolute value equations, let’s go through a detailed process:
Step 1: Isolate the Absolute Value Expression

The first step is to move all terms containing the absolute value to one side of the equation, and all others to the opposite side. Here’s an example:
|2x - 5| = 7
Step 2: Set Up Dual Equations
Once isolated, split the equation into two:
- 2x - 5 = 7
- 2x - 5 = -7
Step 3: Solve Each Equation

Address each equation individually:
- For 2x - 5 = 7
- Add 5 to both sides: 2x = 12
- Divide by 2: x = 6
- For 2x - 5 = -7
- Add 5 to both sides: 2x = -2
- Divide by 2: x = -1
Step 4: Verify the Solutions

After finding your solutions, verify each by substituting back into the original equation:
🔎 Note: Checking your solutions ensures that they do not make the equation undefined (by introducing extraneous solutions).
- Plugging x = 6 into |2x - 5| = |2(6) - 5| = |7| = 7
- Plugging x = -1 into |2x - 5| = |2(-1) - 5| = |-7| = 7
Practice Worksheet: Absolute Value Equations

To practice these concepts, let’s go through a worksheet with several absolute value equations. For each equation, follow the steps outlined above:
| Equation | Solution Steps | Solutions |
|---|---|---|
| |3x - 6| = 9 |
|
5, -1 |
| |2 - 4x| = 10 |
|
-2, 3 |
| |x + 2| + 5 = 1 |
|
No Solution |

Common Pitfalls and Tips

- Be mindful of extraneous solutions when simplifying absolute value expressions.
- Remember to verify your solutions.
- Understand the implications when setting up dual equations.
🎯 Note: Practice and understanding the fundamental property of absolute value being non-negative are key to mastering these types of equations.
We've now navigated through the critical elements of absolute value equations, from understanding the concept to solving complex equations step by step. By breaking down the process and providing a structured worksheet, this guide aims to facilitate learning and enhance problem-solving skills in algebra. Through practice, you'll develop a natural proficiency in solving these equations, understanding that each equation's dual nature provides the opportunity for multiple solutions. Remember to verify your solutions to avoid errors, and always keep in mind the fundamental properties of absolute value. With time and practice, these equations will become less of a challenge and more of an algebraic exercise that broadens your mathematical toolkit.
What is an absolute value?

+
Absolute value is the non-negative value of a real number without regard to its sign. Symbolized by two vertical lines | |, it represents the distance from zero on the number line, making all negative values positive.
Why do absolute value equations have two solutions?

+
Absolute value equations have two solutions because they account for both the positive and negative values of the expression inside the absolute value. For |x| = k, this leads to x = k and x = -k.
How do I solve an equation with multiple absolute values?

+
Multiple absolute values in an equation require you to consider each absolute value independently and then combine all scenarios. This often leads to more than two solutions, and you must check each one for validity.



