7 Key Tips for Translating Quadratic Functions Easily
In the world of mathematics, quadratic functions are fundamental concepts that serve as the backbone of several advanced mathematical applications. Translating quadratic functions, which involve moving the graph of the function left, right, up, or down, can initially seem daunting, but with a few key strategies, this process becomes much more straightforward. Here's how you can master the art of translating quadratic functions with ease.
Understanding Quadratic Functions

Before diving into the translation, let’s understand what a quadratic function is. A quadratic function is typically of the form:
y = ax² + bx + cHere, a, b, and c are constants with a ≠ 0. The graph of a quadratic function is a parabola, symmetrical about its axis of symmetry.
Translating Quadratic Functions

Basic Translation
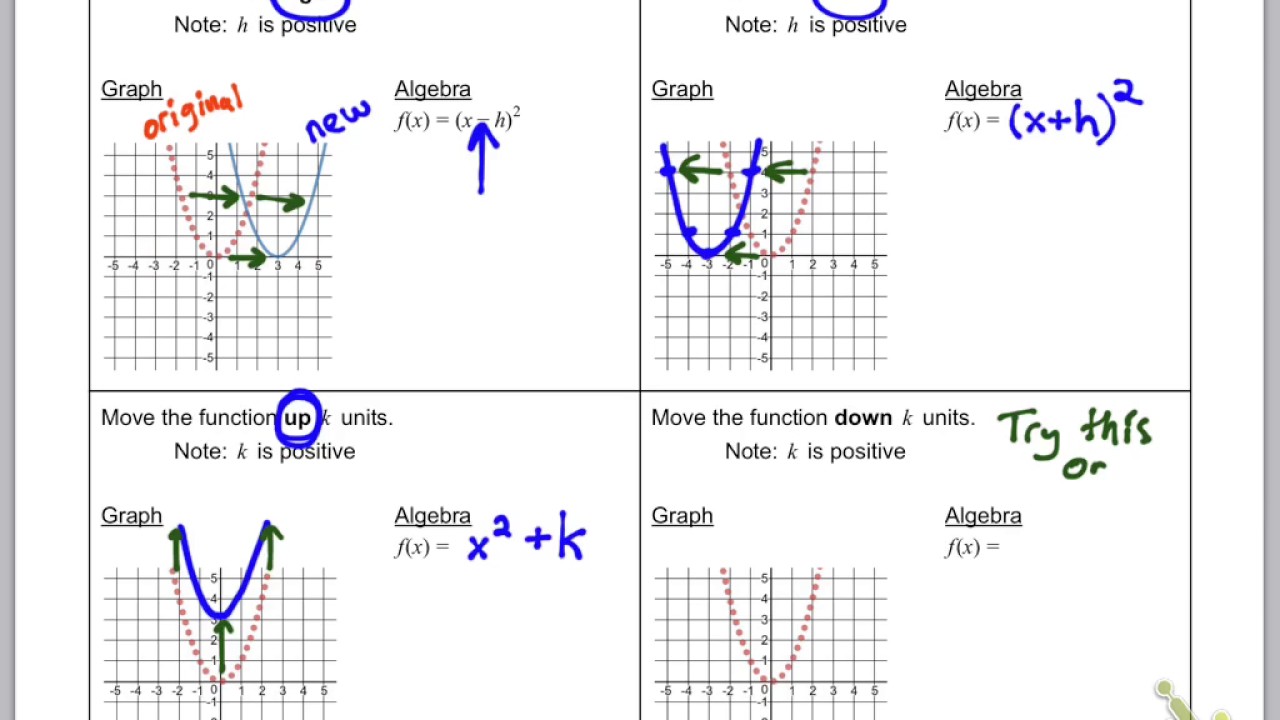
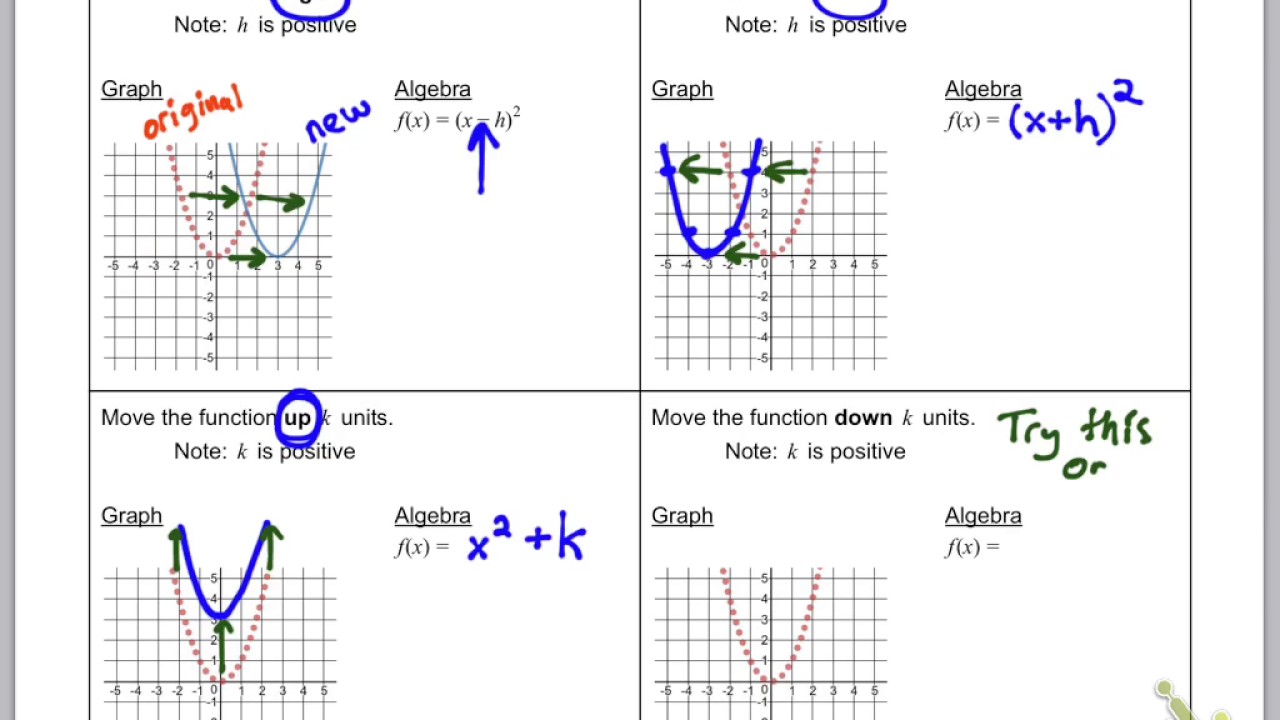
Translation involves moving the parabola without changing its shape or orientation:
- Vertical Translation: Adding or subtracting a constant, k, to the entire equation shifts the graph up or down. If you add k, the graph moves up by k units, and if you subtract, it moves down.
- Horizontal Translation: Adding or subtracting a constant inside the function, h, results in a left or right shift. If you add h, the graph moves to the left by h units, and subtracting moves it to the right.
👉 Note: Remember the rule: f(x - h) + k, where (h, k) is the new vertex position.
Horizontal Shift

To understand how to apply a horizontal shift:
- If the function is y = x² and you need to translate it left by 3 units, your new function will be:
y = (x + 3)²y = (x - 2)²Horizontal shifts directly relate to the input, which is x. By manipulating the x-term, you alter where the function starts or ends.
Vertical Shift

To perform a vertical shift:
- If you want to move the graph of y = x² up by 4 units:
y = x² + 4y = x² - 3📝 Note: Vertical shifts affect the output directly, altering how high or low the graph sits on the coordinate plane.
Combined Shifts

Sometimes, you’ll need to move the parabola both horizontally and vertically at once. Here’s how you do it:
| Initial Function | Translation | Result |
|---|---|---|
| y = x² | 2 units left and 3 units down | y = (x + 2)² - 3 |
| y = x² | 3 units right and 1 unit up | y = (x - 3)² + 1 |

This combination involves modifying both the x and y terms within the function to achieve the desired shift.
Practical Examples

Let’s look at a practical example to solidify these concepts:
- Given the function y = x², translate it 4 units right and 2 units up:
y = (x - 4)² + 2⚠️ Note: Always check your work by plotting the original and the new function on a graph to visually confirm the translation.
Overcoming Common Challenges

When translating quadratic functions, students often face these challenges:
- Direction of Shift: Remember, shifting left or up means adding to the equation, whereas shifting right or down involves subtracting.
- Graphical Representation: Understand that the vertex of the parabola moves in the direction opposite to how x and y terms are affected in the equation.
Wrapping Up
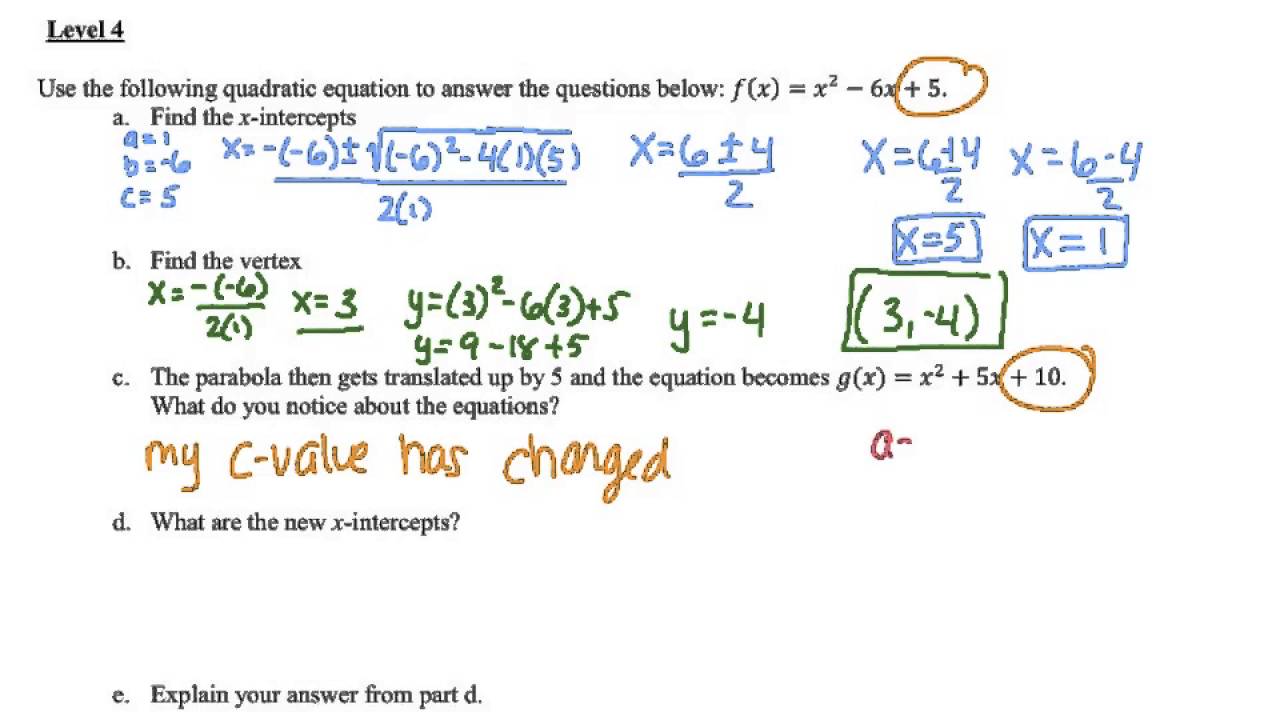
Translating quadratic functions is less about complex calculations and more about understanding how each change affects the parabola. By mastering these translation techniques, you not only enhance your graphical analysis skills but also lay a strong foundation for further algebraic manipulations and problem-solving in higher mathematics.
How does vertical translation affect the function?

+
Vertical translation adds or subtracts a constant to the function’s output. If you add, the graph shifts upwards; if you subtract, it moves downwards. The shape of the parabola remains the same.
What if I need to translate a function to the left and down?

+
Add the units for the left shift inside the function and subtract for the downward movement outside. For instance, f(x) = (x + 3)² - 2 will move the parabola 3 units left and 2 units down.
Can translation change the shape of the parabola?

+
No, translation does not alter the shape of the parabola. It only moves the entire graph. Changing the shape requires modifying the coefficient of x², which affects the stretch or compression.



