Master the Rate of Change with Our Practice Worksheet

Understanding the rate of change is fundamental in various fields such as physics, economics, finance, and engineering. It helps in analyzing how a quantity evolves over time, which can be critical in decision-making processes, predictive modeling, and system optimization. This blog post will guide you through the essential aspects of mastering the concept of rate of change through practice and application.
What is Rate of Change?


Rate of change refers to the relationship between two changing variables, often expressed as a derivative in mathematics. If you imagine plotting a function on a graph, the rate of change at any point would be the slope of the tangent line at that point. Here’s a quick rundown:
- Definition: It is the ratio of the change in one variable to the corresponding change in another variable.
- Mathematical Notation: For functions, it’s commonly denoted as ( \frac{dy}{dx} ) where ( y ) and ( x ) are variables.
- Types:
- Instantaneous rate of change - at a single point.
- Average rate of change - over an interval.
Steps to Calculate Rate of Change

Calculating the rate of change involves several straightforward steps:
- Identify the variables: Determine what variables are changing and which one is the dependent variable.
- Set up the equation: Use the difference formula ( \frac{\Delta y}{\Delta x} ).
- Substitute values: Plug in the values of your variable to calculate the change.
- Calculate: Solve the equation to get the rate of change.
- Interpret the result: Understand what the calculated rate of change means in the context of your problem.
📘 Note: When interpreting results, consider whether the rate of change is instantaneous or average.
Practical Applications of Rate of Change

- Finance: To analyze stock price movements or investment growth rates.
- Physics: Speed and acceleration can be seen as rates of change of distance and velocity, respectively.
- Economics: Understanding how different economic factors like GDP, inflation, or unemployment rate change over time.
- Environmental Science: Studying rates of change in pollution levels, temperature, or species population.
Let’s explore a simple scenario in finance:
| Year | Investment Value (in dollars) |
|---|---|
| 1 | 10,000 |
| 2 | 12,000 |
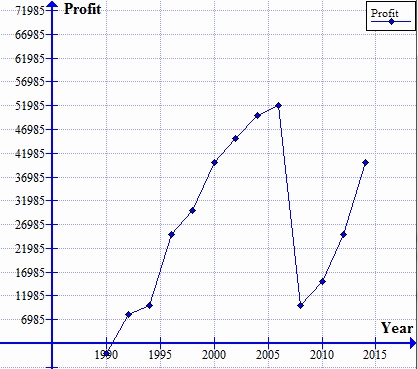
Here, the rate of change in investment value from year 1 to year 2 is calculated as:
[ \frac{12,000 - 10,000}{2 - 1} = 2,000 ]
🌍 Note: This example is simplistic. In real-world scenarios, you would need to account for compounding, inflation, and other financial factors.
Practice Worksheet

To truly master the rate of change, regular practice is crucial. Here’s a basic worksheet to help you get started:
- Question 1: Given the function ( f(x) = x^2 ), find the rate of change at ( x = 3 ).
- Question 2: An object’s position in meters is given by ( s(t) = t^3 - 6t^2 + 9t ). Determine its velocity at ( t = 1 ) seconds.
- Question 3: If the population of a city grows from 5 million to 5.2 million over two years, calculate the annual average growth rate.
💡 Note: These questions should be solved without looking back at previous examples to ensure understanding.
After working through these exercises, you will have a better grasp of calculating and interpreting rates of change. Understanding this concept not only enhances your ability to analyze dynamic systems but also equips you with tools to predict future trends and make informed decisions.
This journey into the rate of change begins with recognizing its importance, followed by learning how to calculate it, and then applying it to real-life scenarios. Remember, the key to mastering this concept lies in consistent practice, thoughtful analysis, and practical application. By engaging with the exercises and problems posed here, you will not only improve your mathematical acumen but also your problem-solving skills across various disciplines.
What is the difference between instantaneous and average rate of change?
+
The instantaneous rate of change is the rate at a specific point, while the average rate of change is calculated over an interval, giving an average of how one variable changes with respect to another over that interval.
How can the rate of change be applied in real-world scenarios?

+
Rate of change is used in many fields to analyze trends and make predictions. For example, in finance, it can predict stock price movements; in physics, it calculates velocity and acceleration; in economics, it measures changes in inflation, GDP, etc.
What are common mistakes when calculating the rate of change?

+
Common mistakes include confusing units, using the wrong formula for the context, not interpreting the result correctly, or miscalculating changes in the variables due to arithmetic errors.